Стоки – катушка индуктивности

Если заменить резисторную сетку на реактивную катушку индуктивности вместо резисторов, получаем модель для волнового уравнения

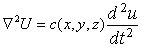(7.21)

которое может быть применено для моделирования электромагнитных полей, исследования других колебаний и т.п.

Таким образом возможность введения стоков и источников значительно расширяет круг задач, решаемых методом электрических сеток, по сравнении с методом сплошных сред.

1.2.4. Решение задач подземной гидравлики нефтяных месторождений

Очень показательным примером широкого практического применения сеточного моделирования явилось решение задач подземной гидравлики нефтяных месторождений [55]. Нефтяной пласт представляет собой пористую среду пропитанную нефтью, которая движется под действием перепада давлений между внешним контуром питания и скважинами. Величина дебитов отдельных скважин зависит от распределения давлений, которое, в свою очередь, зависит от расположения и взаимного влияния скважин. Ставится задача определения дебитов скважин при их оптимальном расположении, которая может быть представлена в виде решения уравнения электрического типа.

Моделируемое поле представляется по форме нефтяной залежи, на контуре питания и на скважинах устанавливаются потенциалы, пропорциональные давлениям. Относительно малая (по сравнению с площадью) толщина пласта позволяет рассматривать задачу как двумерную, выполняя модель в виде слоя переменной толщины. На рис.7.12 представлен фрагмент такой модели в виде электрической сетки. Гидравлические сопротивления скважин моделируются с помощью добавочных сопротивлений 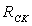в цепи тока. Токи в этих сопротивлениях являются аналогами дебита скважин.

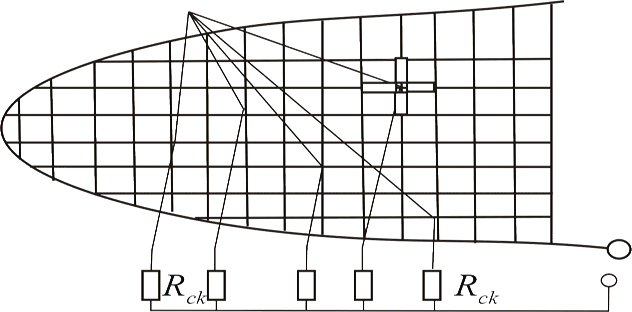
Рис. 7.12 Сеточная модель нефтяного месторождения

Моделирование одного из действующих нефтяных месторождений, на котором было набурено около ста скважин, показало, что половину из этих скважин не нужно было бурить, то есть такой же суммарный дебит могли обеспечить 50 скважин. Многомиллионные затраты на бесполезные и даже “вредные” скважины, просто снижающие давление пласта, очень наглядно подчеркнули эффективность использования методов математического моделирования и невозможность решения такого рода задач по “наитию”. Следует подчеркнуть, что упомянутая выше модель представляла собой весьма сложную систему из восьмисот уравнений, которые решились на гибридном (аналого-цифровом) комплексе. Этот подход в дальнейшем получил достаточно широкое развитие на новом научном и техническом уровне применительно к современным цифровым ЭВМ, быстродействие которых за последние годы сильно возросло.

1.3. Метод конечных элементов

Одной из широко распространенных направлений такого подхода (также основанного на принципе прямой аналогии) является метод конечных элементов. Не останавливаясь здесь на описании этого метода, мы несколько ниже рассмотрим пример его реализации с использованием системы компьютерной математики ”MATLAB”.

2. Модели полей тепло и массопереноса на табличном процессоре Excel

2.1. Использование табличного процессора Excel

Большинство пользователей персональных ЭВМ знакомо с замечательными свойствами электронных таблиц, в которых с помощью определенных математических соотношений можно связать ячейки таким образом, чтобы при изменении числовых данных в одних ячейках автоматически менялись результаты также в других связанных с ними ячейках. Во многих случаях применение табличного процессора Excel, входящего в состав основного программного обеспечения Microsoft Office, ограничивается сравнительно простыми вычислениями типа калькуляционных. Однако на самом деле в этом процессоре кроются огромные возможности, которые представляются при квалифицированном использовании встроенного в него внутреннего оптимизатора. При этом становится возможным превратить ячейки электронных таблиц в цифровой аналог рассмотренных выше элементов замещения поля и таким образом решать задачи, описываемые уравнениями в частных производных. Пример такой задачи приведен ниже.

2.2. Моделирование процесса теплообмена в трехмерном приближении

Для математического описания теплообмена трехмерного тела с геометрической областью 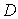и кусочно-гладкой границей 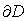использованы модели в виде краевых задач математической физики III рода для дифференциального уравнения с частными производными параболического типа в случае нестационарного теплообмена:

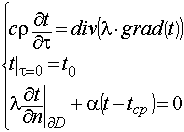(7.22)

и для уравнения эллиптического типа — в случае стационарного теплообмена:

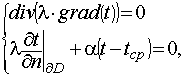(7.23)

где 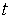, 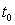– текущее и начальное распределения на 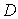температуры тела, 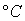, 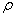— распределение на 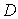плотности материала тела, 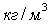; 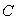— распределение на 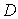удельной теплоемкости материала тела, 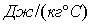; 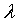-распределение на 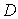коэффициента теплопроводности материала тела, 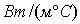; 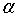— распределение на 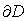коэффициента теплоотдачи со стороны как греющей, так и охлаждающей сред, 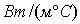; 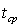– распределение на 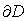температуры окружающей среды, 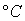; 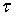– время, с; 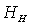– внешняя нормаль к границе тела .

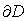2.3. Особенности методики расчета и реализации на ЭВМ трехмерных задач теплообмена

2.3.1. Особенности

Особенность методики решения задачи заключается в разработке соответствующих Excel-приложений на языке визуального и событийно-управляемого программирования VBA (Visual Basic for Application) в составе Microsoft Office 97 операционной системы Windows, реализующих алгоритмы расчета, соответствующие математическим моделям (7.22) и (7.23).

2.3.2. Основные этапы методики

Основные этапы методики сводятся к следующему:

1. Анализ геометрии исследуемого трехмерного тела и выделение на основе принципов симметрии расчетной области 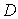для постановки краевых задач.

2. Разбиение расчетной области 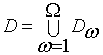на элементарные непересекающиеся однотипные подобласти 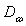с учетом особенностей исходной геометрии .

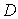3. Аппроксимация задач (7.22) и (7.23) соответствующей конечно-разностной задачей с помощью метода конечных разностей.

4. Разработка и реализация в модулях Excel-приложений на VBA итерационных типовых алгоритмов решения конечно-разностных уравнений для областей 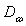. Расчет распределений температуры в трехмерной области производится набором процедур в модулях VBA с использованием трехмерных структур данных (например, массивов).

5. Проектирование и реализация интерфейса пользователя путем создания соответствующих диалоговых окон, элементов управления и диаграмм для оперативного управления процессом вычислительного эксперимента и анализа его результатов в виде как числовой, так и графической информации. Параметрами оперативного управления являются как теплофизические характеристики горячих сред и охладителей, так и конструктивные параметры охлаждаемых элементов исследуемых объектов. Данные для визуализации распределения температуры формируются на листах табличного процессора Excel с помощью процедур извлечения двумерных структур данных в соответствии с интересующими сечениями трехмерной расчетной области. Эти процедуры так же находятся в модулях VBA. На основе двумерных структур данных формируются диаграммы распределения температурных полей в сечениях, которые компонуются в виде документа, характеризующего в целом распределение температуры по объему тела.

6. Формирование критерия оптимизации в соответствии с требуемой естественно-физической постановкой задачи и реализация поставленной оптимизационной задачи с помощью оптимизатора (Solver) табличного процессора Excel.

Исследование теплообменных процессов в плоской стенке при охлаждении с помощью специальных охлаждаемых элементов

2.3.3. Исследование температурных полей в медной плоской стенке

Применение описанной выше методики рассмотрено [57] на примере исследования температурных полей в медной плоской стенке толщиной 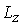охлаждаемой с помощью специальных элементов охлаждения, в которых циркулирует в качестве охладителя вода с температурой 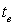и которые конструктивно вмонтированы в специальные посадочные гнезда глубиной 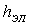, расположенные на стенке с охлаждаемой стороны равномерно, т.е. в вершинах квадратов, на расстоянии 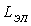между центрами элементов. Нагрев стенки осуществляется с противоположной стороны за счет контактирования с горячим газом, температура которого равна 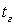. Задача решается в декартовом приближении. Сечение элемента водоохлаждения представляет собой квадрат, сторона которого равна 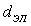. Фрагмент стенки с выделенной расчетной областью представлен на рис.7.13.

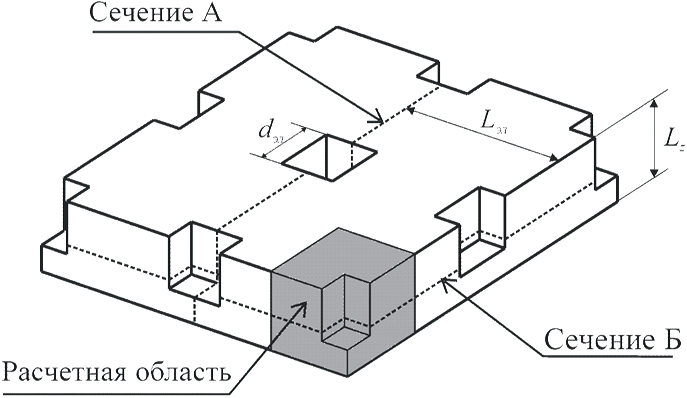
Рис. 7.13 Фрагмент плоской стенки с посадочными гнездами для элементов охлаждения

Для конечно-разностной аппроксимации краевых задач область 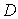покрыта равномерной по каждой кординате сеткой с шагами 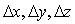,и индексацией узлов с помощью индексов 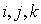,по соответствующей координате. По времени выбран шаг дискретизации .

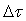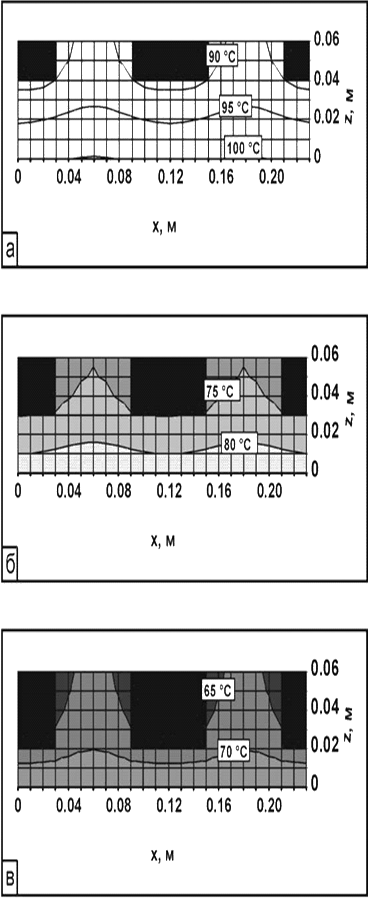
Рис. 7.14 Температурные поля в сечении , проходящем через центры элементов водоохлаждения при значениях глубины посадки: а) 0,02 м; б) 0,03 м; в) 0,04 м

На рис.7.14 представлены распределения температуры в сечении 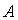(рис.7.13), проходящем через центры элементов водоохлаждения, для случаев трех значений глубины 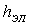посадки элементов водоохлаждения: 0,02 м, 0,03 м, 0,04 м. При этом основные конструктивные размеры имели следующие значения: 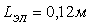, , 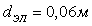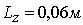.Значения температур, приведенные на диаграммах, соответствуют значениям температур на изолиниях. Температура газа равна 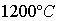, воды — 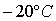. Коэффициент теплоотдачи со стороны газа определялся на основании теории лучистого теплообмена и принимал значения в рассматриваемых трех случаях от 70 до 75 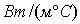, со стороны воды коэффициент теплоотдачи задавался равным 2000 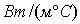. Распределение температуры в сечении Б (рис.7.13), проходящем через середину толщины стенки, для тех же случаев представлено на рис. 7.15.

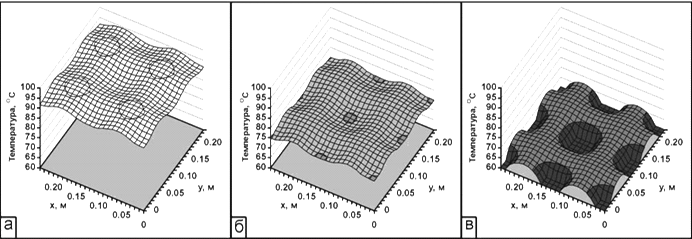
Рис. 7.15 Температурные поля в сечении , проходящем через середину толщины плоской стенки при значениях глубины посадки элементов водоохлаждения: а) 0,02 м; б) 0,03 м; в) 0,04 м

Анализ приведенной графической информации в серии расчетов в совокупности с решением оптимизационных задач позволяет правильно выбрать как режимы охлаждения, так и конструктивные решения при проектировании систем охлаждения технологическими агрегатами.

Заключение

В данном реферате были рассмотрены методы моделирования пластов, особое внимание было уделено сеточному методу моделирования пластов. Также рассмотрены особенности методики расчета и реализации на ЭВМ трехмерных задач теплообмена.

Список использованной литературы

1. Научные школы СибГИУ, «МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ, СОЗДАНИЕ ПРИКЛАДНЫХ ИНСТРУМЕНТАЛЬНЫХ СИСТЕМ И НОВЫХ МЕТАЛЛУРГИЧЕСКИХ ПРОЦЕССОВ И АГРЕГАТОВ НА ПРИНЦИПАХ САМООРГАНИЗАЦИИ», Новокузнецк, 2015

2. Х. АЗИЗ, Э. СЕТТАРИ, «МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПЛАСТОВЫХ СИСТЕМ», Москва Ижевск 2004