Игры с ненулевой суммой и кооперативные игры

В игре с ненулевой суммой, уже необязательно, чтобы один из участников выигрывал, а другой проигрывал; напротив они могут и выиграть, и проигрывать одновременно. Поскольку интересы игроков теперь не являются полностью противоположными, их поведение становится более разнообразным.

Так, например, в игре с нулевой суммой каждому игроку было невыгодно сообщать другому свою стратегию (это могло уменьшить их выигрыш) то в игре с ненулевой суммой становится желательным как-то координировать свои действия с партнером или каким-либо способом влиять на его действия.

Игры с ненулевой суммой могут быть кооперативными и некооперативными. В некооперативных играх игроки принимают решения независимо друг от друга, либо потому, что осуществление соглашения невозможно, либо потому, что оно запрещено правилами.

Пример. Игра Дилемма Заключенного представляет пример игры двух лиц с ненулевой суммой, в которой взаимодействие игроков невозможно по условиям игры.

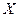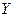Один из подходов к решению некооперативных игр состоит в определении точек равновесия игры. Понятие равновесия в теории игр шире понятия оптимальности в теории оптимизации и включает последнее как частный случай. В общем, пара стратегий и для Игрока 1 и Игрока 2 называется точкой равновесия по Нэшу, если ни одному из игроков невыгодно отклоняться от своей стратегии в одиночку, т.е. если

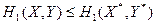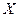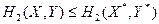для любых и для любых .

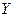Это уравнение равновесия сохраняется и для 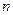лиц.

Пример: Рассмотрим матрицу выигрышей, которая имеет вид: .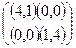

В данной игре игры стратеги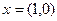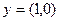й ; и 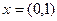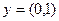являются равновесными, т.е. Игроку 2(1) не выгодно отклоняться от первой (второй) стратегии, если Игрок 1(2) придерживается первой (второй) стратегии. Следует отметить, что выигрыши в равновесных точках различны.

Для любой конечной некооперативной игры с ненулевой суммой (называемой также биматричной игрой) всегда существует, по крайней мере, одна равновесная игра смешанных стратегий. В общем случае равновесное решение может быть неединственным, и каждому из них могут соответствовать различные значения выигрыша каждого из игроков.

Кооперативной игрой называется игра с ненулевой суммой, в которой игроком разрешается обсуждать перед игрой свои стратегии и договариваться о совместных действиях, т.е. игроки могут образовывать коалиции. Основная задача в кооперативной игре состоит в делении общего выигрыша между членами коалиции.

В случае игры двух лиц предполагается, что два игрока не могут воздействовать друг на друга, пока не придут к некоторому соглашению. Таким образом, игра определяется как множество 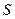в пространстве переменных 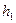и 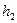, представляющие общие выигрыши.

Кроме того заданы два числа 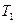и 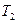, определяющие величины выигрыша, которые каждый из игроков может получить не вступая в коалицию со своим партнером.

Обычно полагают, что множество 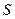является замкнутым, выпуклым и ограниченным сверху. Точка 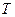с координатами 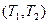называется точкой угрозы.

На множестве возможных выигрышей выделяется множество Парето - оптимальных решений, т.е. множество точек принадлежащих 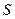, для которых увеличение выигрыша одного из игроков возможно только за счет уменьшения выигрыша партнера. Очевидно, что множество таких точек образует северо-восточная граница множества .

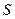Все точки Парето - оптимального множества, находящиеся одновременно выше и правей точки 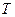, образуют, так называемое, - переговорное множество.

Очевидно, что игрокам, нет смысла договариваться относительно решений, не принадлежащих переговорному множеству, либо потому, что положение одного из игроков может быть улучшено при сохранении положения его партнера и можно договариваться о более выгодных решениях либо потому, что, по крайней мере, для одного из игроков теряет смысл вступать коалицию со своим партнером – не худших результатов он может достигнуть в одиночку.

На переговорном множестве выделяется точка 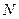, в которой достигается максимум произведения превышения выигрышей каждого из игроков над платежами, которые могут быть получены без вступления в коалицию max /

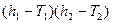В теории игр доказывается, что если множество возможных платежей 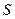выпукло, замкнуто и ограничено сверху, то точка Нэша 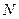существует и единственна. Точка Нэша представляет одно из возможных решений кооперативной игры, от которого нет оснований отказываться ни одному из игроков.

Рассмотрим пример игры над названием.

Семейный спор.

Согласно условиям этой игры семейная пара Муж и Жена каждый вечер решают проблему: как им провести свой досуг. В городке, где они живут, имеется два вида развлечений: Балет и Футбол. У каждого из супругов есть свое любимое зрелище: Жена предпочитает – балет, Муж – футбол.

Однако супруги так привязаны друг к другу, что посещение любимого развлечения в одиночку доставляет им совсем не такое удовольствие как присутствие на них вдвоем, т.е е если Жена идет вечером на балет с Мужем, она получает максимум удовольствия (4 единицы). Муж недолюбливает балет, но присутствие на нем с Женой спрашивает тягостное времяпровождение (1 единица). История повторяется с точностью до наоборот, когда Жена идет с Мужем на обожаемый им футбол.

Муж получает (4 единицы), Жена получает (1 единицу). В принципе Муж может сходить на Футбол один, а жена в одиночку сходить на балет (за это они получат по 2 единицы). И вечер будет испорчен, если Муж пойдет на футбол, а жена на балет (0 единиц).

В итоге матрица выигрышей описанной игры будет:

Муж	Жена
	Балет	Футбол
Балет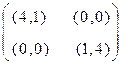
Футбол

Можно показать, что если супруги будут придерживаться различных несогласованных стратегий, множество возможных выигрышей образует в системе треугольник 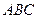с вершинами в точках , , .

		В

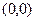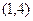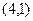Линия 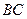- множество Парето - оптимальных решений. Вдоль этой линии рост удовольствий Жены, возможен только за счет снижения удовольствия Мужа.

Точка 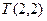- является точкой угрозы в этой игре. Например, «угроза» со стороны Жены может звучать: «Вместо того чтобы более 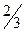своего свободного времени проводить на этом футболе, а буду ходить на балет (с Мужем или без него – неважно) – ничего не потеряю.

Аналогично может звучать «угроза» - Мужа.

Переговорное множество, образуемое точкой угрозы 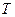, представлено линией 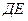, образуемое точкой угрозы 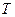, представлено линией 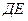, на Парето - оптимальном множестве решений 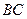. На линии 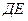Муж и Жена могут договариваться, как часто они будут бывать вместе на одном из зрелищ, но при этом, во избежание взаимных угроз ни одному из развлечений не должны уделить более своих свободных вечеров.

Решение Нэша, когда максимально произведение приростов удовольствия Мужа и Жены по сравнению с удовольствием от независимого посещения Футбола и Балета, представлено точкой 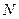- супруги договариваться половину своего свободного времени проводить вместе на балете, вторую половину – на футболе.