Формулировка задачи линейного программирования
Применение математических методов в экономике обосновано тем, что работа любого экономического объекта (цех, предприятие, фирма, компания и т.п.) может быть охарактеризована с экономической точки зрения некоторыми числовыми характеристиками. Это могут быть объем выпускаемой продукции или затрачиваемых ресурсов (сырья, времени и т.д.), величина прибыли или расходов и т.п. Обычно из числа этих величин выбирают некоторую группу, которую называют планом, а каждую величину, включенную в план – компонентой плана. Компоненты плана, очевидно, не могут принимать какие угодно значения. Они изменяются в некоторых пределах, образуя в целом множество или область планов. Планирование работы данного объекта состоит в выборе одного плана из этого множества. Но чтобы мотивировать выбор того или иного плана, надо иметь какой-то критерий, позволяющий оценивать планы, что делается обычно с учетом поставленной цели. Такой целью, например, может быть получение возможно большей прибыли, или затрата возможно меньшего количества средств и т.п. Для оценки степени достижения цели и сравнения с этой точки зрения различных планов выбирают некоторую величину, значения которой меняются в зависимости от выбранного плана. Следовательно, речь идет о выборе некоторой функции плана, её обычно называют целевой функцией. С помощью этой функции можно сравнивать, оценивать планы. Например, если функция выражает прибыль, то, естественно, тот план лучше, который обеспечивает большую прибыль, если целевая функция – это расходы, то тот план лучше, который обеспечивает меньшее значение расходов. Наиболее выгодный с точки зрения экономического эффекта план называется оптимальным планом. Значение целевой функции соответствующее оптимальному плану, называют её оптимальным значением. Чаще всего оптимальным значением целевой функции является её экстремальное значение, т.е. наибольшее или наименьшее среди всех её возможных значений.
Итак, выбор наилучшего плана означает отыскание оптимального значения целевой функции в области всех возможных планов. Такую задачу легко сформулировать математически, построив экономико-математическую модель, и свести, таким образом, вопрос об оптимальном планировании к решению этой задачи.
В общем виде задача математически записывается в виде:
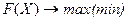 ;
; 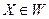 ,
,
где 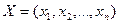 ;
;
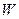 - область допустимых значений переменных
- область допустимых значений переменных 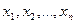 ;
;
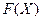 - целевая функция.
- целевая функция.
Для того чтобы решить задачу оптимизации, достаточно найти её оптимальное решение, т.е. указать 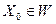 такое, что
такое, что 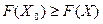 при любом
при любом 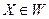 для случая максимизации и
для случая максимизации и 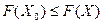 при любом
при любом 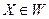 для случая минимизации.
для случая минимизации.
Методы решения оптимизационных задач зависят как от вида целевой функции 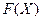 , так и от строения допустимого множества
, так и от строения допустимого множества 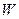 . Если целевая функция в задаче является функцией
. Если целевая функция в задаче является функцией 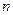 переменных, то методы решения называют методами математического программирования.
переменных, то методы решения называют методами математического программирования.
В математическом программировании принято выделять задачи в зависимости от вида целевой функции 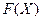 и от области
и от области 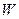 :
:
- задачи линейного программирования, если 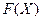 и
и 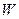 линейны;
линейны;
- задачи целочисленного программирования, если ставится условие целочисленности переменных 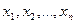 ;
;
- задачи нелинейного программирования, если форма 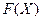 носит нелинейный характер.
носит нелинейный характер.
