О влиянии на движение искусственного спутника Земли возмущающих факторов негеопотенциальной природы

Следует сразу отметить, что эти вопросы с необходимой детальностью обсуждаются в параграфах 47, 48, 49 хорошо известного учебника [КГ], что позволяет здесь, в основном следуя указанным параграфам, конспективно остановиться лишь на наиболее значимых возмущающих факторах.

Влияние притяжения Луны и Солнца.

Одной из причин, возмущающих обращение ИСЗ вокруг Земли, является гравитационное притяжение Луны, Солнца и других небесных тел. Поскольку в силу удаленности названных объектов это влияние не слишком велико (в частности, влияние притяжения Луны на движение ИСЗ примерно в 10000 раз меньше, чем влияние полярного сжатия Земли), в нашем случае возможно рассматривать Луну и Солнце как точечные массы, а притяжением других планет в большинстве случаев пренебречь. Это означает, что и влияние Луны, и влияние Солнца описывается однотипными формулами, получаемыми на основании соотношений подробно изучаемой в небесной механике ограниченной задачи трех тел, в роли которых выступают Земля, Луна (или Солнце, или планета) и ИСЗ пренебрежимо малой массы. 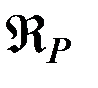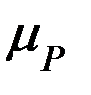Обозначим пертурбационную функцию и гравитационную постоянную GM возмущающего тела P (Луны, Солнца, планеты) символами и соответственно, а его геоцентрическое расстояние - 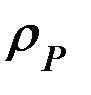. Тогда в ограниченной задаче трех тел пертурбационная функция притяжения тела нулевой массы возмущающим телом будет иметь вид:

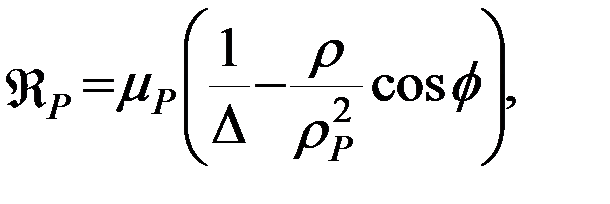(5.5.1)

где символом ρ обозначено геоцентрическое расстояние ИСЗ, символом Δ– расстояние между ИСЗ и возмущающим телом P, а символом ϕ – плоский угол между геоцентрическими направлениям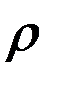и и 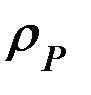на спутник и возмущающее тело. Поскольку для нашего случая всегда выполняется условие 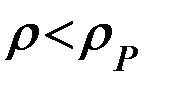, функция обратного расстояния Δ может быть представлена сходящимся рядом по полиномам Лежандра:

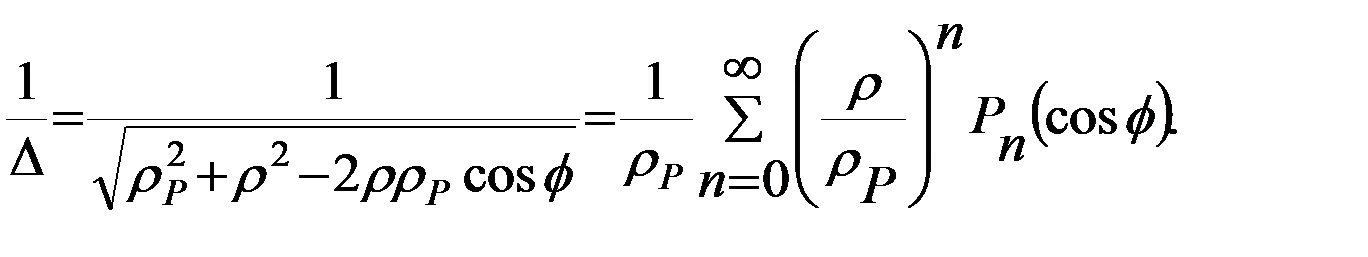
Тогда

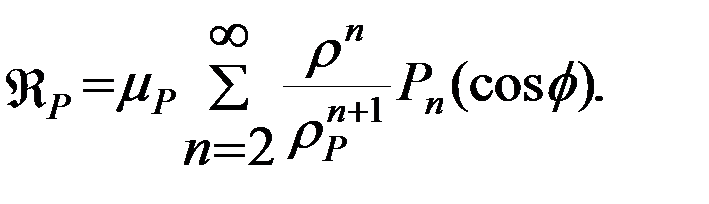
В этой формуле первое слагаемое ряда при n=0отброшено, поскольку оно не зависит от координат ИСЗ и потому обращается в нуль при дифференцировании пертурбационной функции по координатам спутника. Второе слагаемое ряда приn=1взаимно уничтожается со вторым членом в круглых скобках формулы (5.5.1). Поскольку cosϕ есть функция геоцентрических экваториальных координат (прямого восхождения и склонения) ИСЗ α,δи возмущающего телаα_P,δ_P, теорема сложениясферических функций позволяет записать:

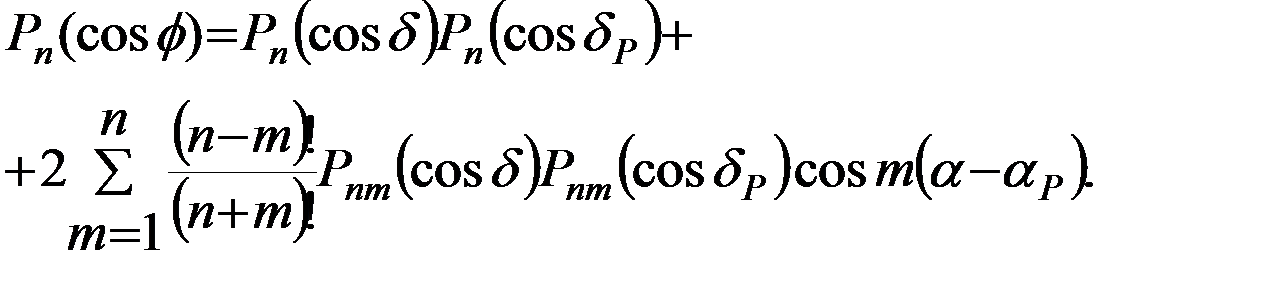
Тогда пертурбационная функция притяжения ИСЗ возмущающим телом Рпримет вид:

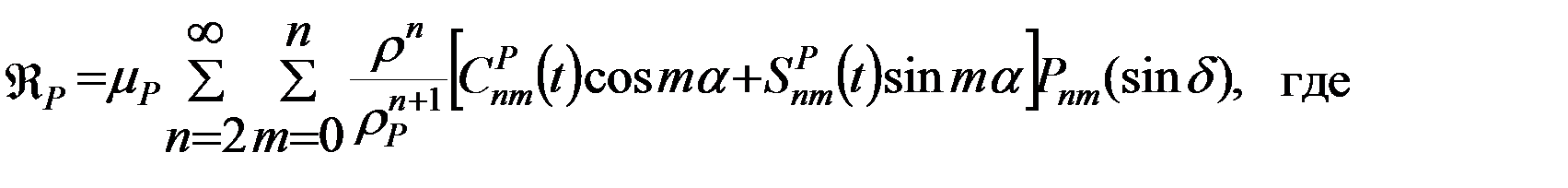(5.5.2)

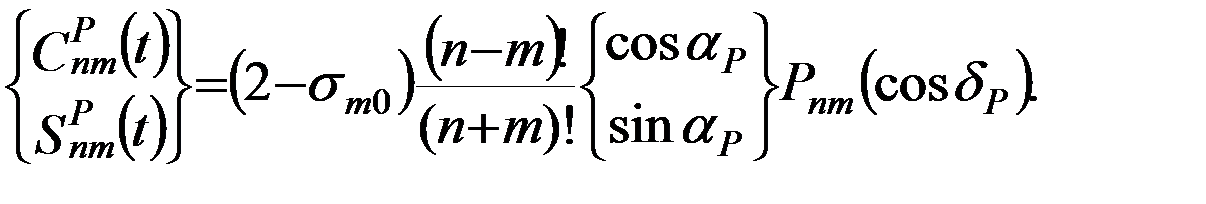
Удобство формул (5.5.2) состоит в разделении быстро и медленно изменяющихся переменных: коэффициенты 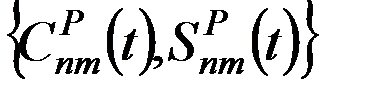разложения (5.5.2) содержат только геоцентрические экваториальные координаты удаленного возмущающего тела и потому изменяются медленно, вследствие медленного его движения относительно Земли. Удаленность возмущающего тела позволяет также при суммировании ряда (5.5.2) ограничиться 2-5 первыми членами для Луны и 1-3 членами для Солнца.

Влияние лунно-солнечных приливов.

В силу того, что Земля не является абсолютно твердым недеформируемым телом, значительная часть ее покрыта водой, а вся она окружена атмосферой, гравитационное притяжение движущихся относительно Земли третьих тел (Луна, Солнце, планеты) приводит к деформации фигуры Земли и изменениям ее гравитационного поля, которые должны быть учтены в процессе оценивания численных значений параметров модели геопотенциала. Заметим, что среди гравитационных возмущений теория учета приливных эффектов является наиболее сложной. Дело в том, что на современном уровне точности требуется учитывать не только приливы в твердом теле Земли, но также океанические, полюсные и атмосферные приливные эффекты.

В настоящее время согласно рекомендациям Международной службы вращения Земли (IERS) 2010 г. [http://62.161.69.131/iers/conv2010/conv2010] учет приливных деформаций выполняют путем внесения зависящих от времени малых поправок 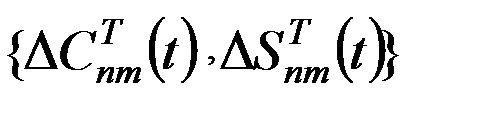в гармонические коэффициенты 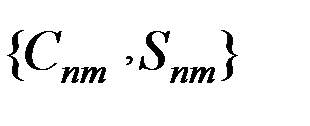модели гравитационного потенциала Земли:

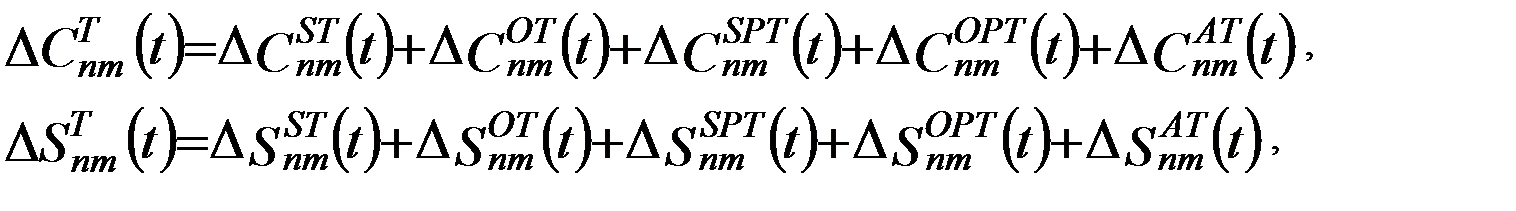
где для поправок приняты обозначения:

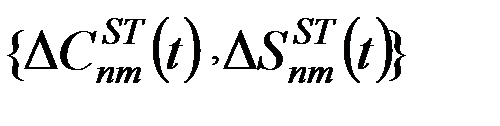- совокупность поправок за влияние твердых земных приливов,

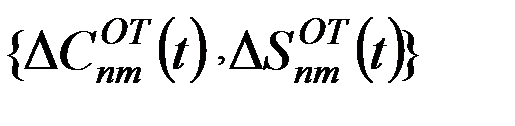- совокупность поправок за влияние океанических приливов,

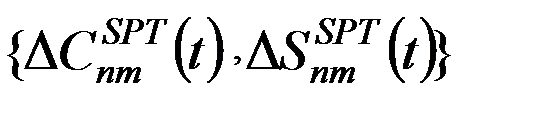- совокупность поправок за влияние твердого полюсного прилива,

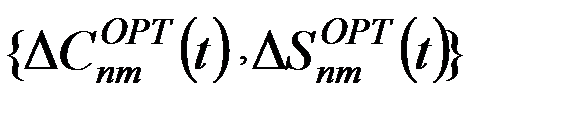- совокупность поправок за влияние океанического полюсного прилива,

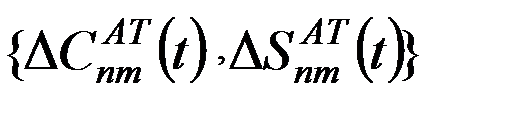- совокупность поправок за влияние атмосферных приливов.

Уместно напомнить, что термин «полюсный прилив» был введен основоположником современной теории приливов Д.Дарвином, который таким образом обозначил приливные волны в теле и океанах Земли, обусловленные изменением центробежной силы при нутационных колебаниях мгновенной оси вращения нашей планеты. Нестабильность вращенияЗемли (изменения скорости ее вращения и изменения положения полюсов) порождает в океане и атмосфере полюсной прилив, который,взаимодействуя с лунно–солнечными приливами,влияет на движения атмосферы и океана и протекающие в них процессы.

Явный вид формул для вычисления приливных поправок 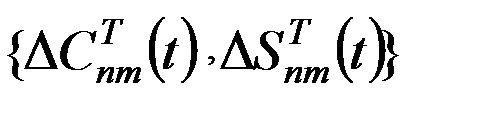приведен на сайте Международной службы вращения Земли (IERS-2010): [http://62.161.69.131/iers/conv2010/conv2010], [ftp://tai.bipm.org/iers/conv2010/chapter6/tn36_c6.pdf].

Влияние светового давления.

Возмущающее ускорение, возникающее вследствие давления солнечных лучей на поверхность ИСЗ, вычисляется по формуле [Колегов]:

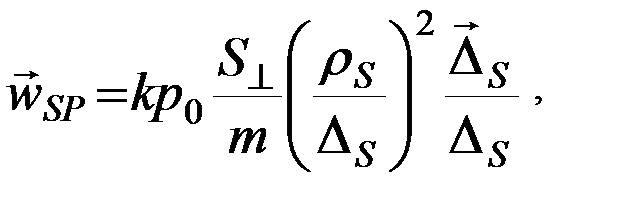(5.5.3)

где:

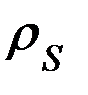– геоцентрический радиус-вектор Солнца (среднее расстояние от Земли до Солнца),

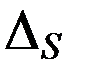– спутникоцентрический радиус-вектор Солнца,

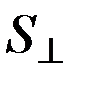- площадь миделевого сечения - поперечного сечения ИСЗ плоскостью, перпендикулярной к векторулинейнойскорости спутника,

m – масса спутника,

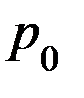– давление солнечных лучей в районе орбиты Земли,

k – коэффициент, принимающий значения от единицы до двух, и зависящий от геометрии ИСЗ и отражающих свойств его поверхности.

Примем обозначение:

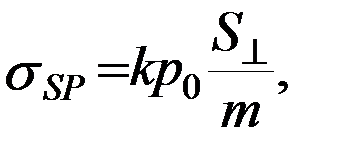тогда модуль вектора возмущающего ускорения будет равен 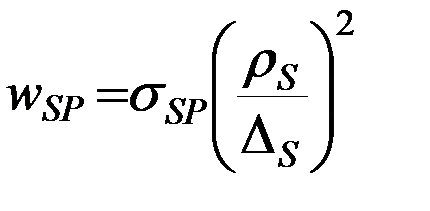, а его пертурбационная функция: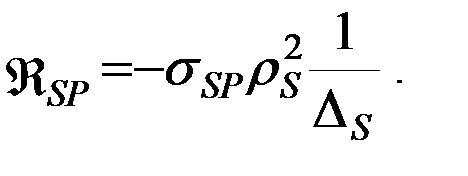

Заметим, кстати, что пертурбационная функция (потенциал силы) светового давления пропорциональна функции обратного расстояния, аналогично потенциалу силы притяжения точечной массы (с обратным знаком). Раскладывая функцию 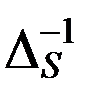обратного расстояния от спутника до Солнца в ряд полиномов Лежандра 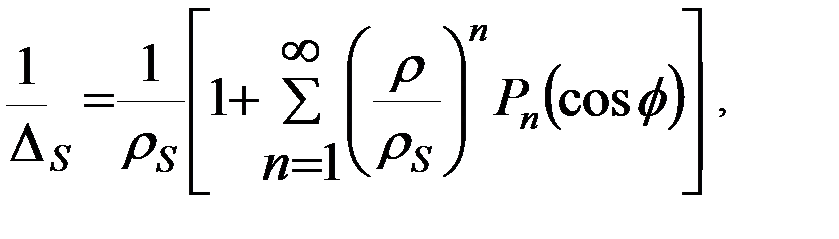а также отбрасывая первое слагаемое разложения, поскольку оно не зависит от координат спутника и при дифференцировании по координатам ИСЗ будет равно нулю, получим для пертурбационной функции светового давления Солнца:

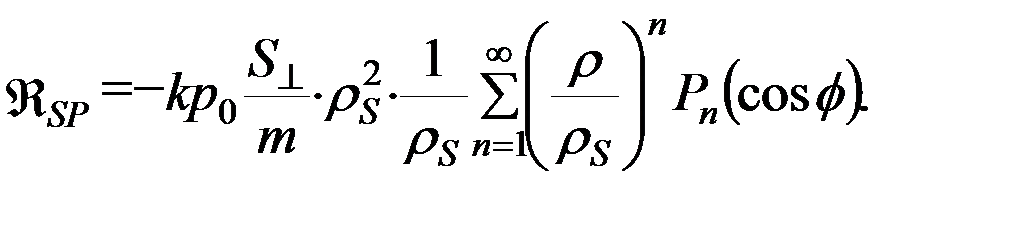(5.5.4)

В силу удаленности Солнца в большинстве случаев достаточно ограничиться первым членом разложения (5.5.4).

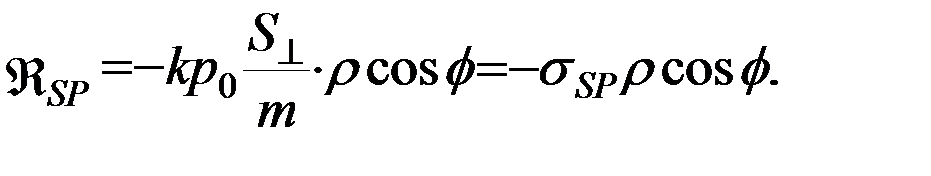(5.5.5)

Понятно, что воздействие силы светового давления имеет место лишь в случае прямого освещения спутника солнечными лучами. При уходе ИСЗ в тень Земли это радиационное влияние прекращается (остается лишь тепловое переизлучение Земли, которое меньше, примерно, в три раза). Учет указанного обстоятельства осуществляется введением в пертурбационную функцию (5.5.5) дополнительного сомножителя 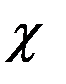, называемого теневой (релейной) функцией, которая равна единице, когда спутник освещен Солнцем, и равна нулю, когда он находится в тени. На высоте около 550км солнечное давление становится примерно равным силе атмосферного сопротивления.

Также можно напомнить, что давление солнечного света открыто П.Н.Лебедевым, который одновременно показал, как уже отмечалось выше, что силы солнечного давления и солнечного притяжения могут быть описаны одинаковыми уравнениями. Иными словами, равнодействующая сила 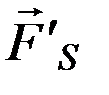, воздействующая на ИСЗ со стороны Солнца, равна разности силы 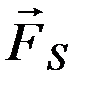ньютоновского притяжения и силы светового давления 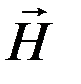Солнца, то же справедливо в отношении пертурбационных функций (потенциалов этих сил):

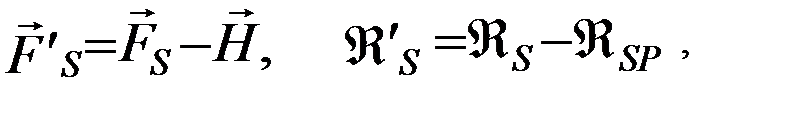
где символом 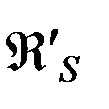обозначена пертурбационная функция совместного действия притяжения Солнца и светового давления солнечных лучей. Данное обстоятельство может быть использовано при численном интегрировании уравнений движения ИСЗ.

Влияние атмосферного торможения.

Вектор силы сопротивления, которая возникает при движении материального тела в газовой среде, описывается аэродинамической формулой:

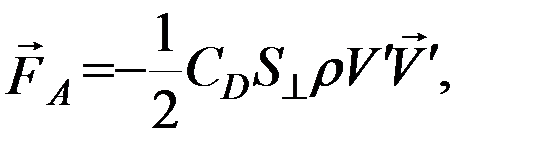(Ю)

где 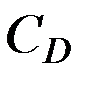- аэродинамический коэффициент, примерно равный 2.15 для всех значений скоростей и высот, 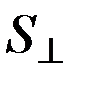- площадь миделевого сечения - поперечного сечения ИСЗ плоскостью, перпендикулярной к вектору 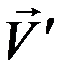линейнойскорости спутника относительно атмосферы, ρ – плотность атмосферы на высоте полета. Введение так называемого возмущающего параметра 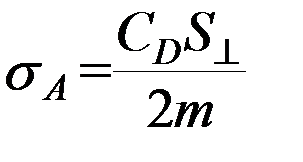позволяет переписать формулу (Ю) для вектора возмущающего ускорения, обусловленного влиянием атмосферы:

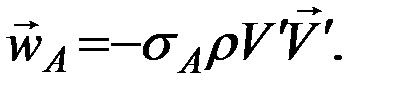Знак минус, очевидно, отражает тормозящий характер возмущающего ускорения.

Плотность ρ, вообще говоря,представляет собой сложную функцию, зависящую от высоты полета, географической широты подспутниковой точки (эллиптичности атмосферных слоев), времени суток, солнечной активности, магнитных бурь и ряда других факторов. В первом приближении, как правило, используется экспоненциальная зависимость плотности атмосферы от высоты полета h, отсчитываемой от перицентра, т.е. 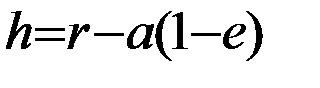, где r в данном случае – геоцентрический радиус-вектор спутника, а 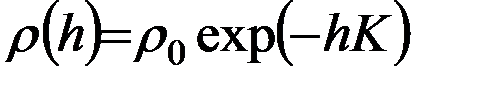, где, в свою очередь, 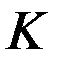- коэффициент пропорциональности, а 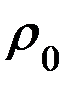- плотность атмосферы Земли на высоте перигея.

Понятно, что для решения динамических задач, связанных с построением максимально точной теории движения ИСЗ, предпочтительно использование заатмосферных спутников с высотой не менее 2000 км и малым отношением 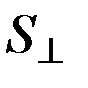/ m (так называемых «тяжелых» спутников).

Поскольку, как уже отмечалось выше, сила атмосферного торможения (Ю) не имеет потенциала, получим необходимые для дальнейшего численного интегрирования проекции вектора возмущающего ускорения 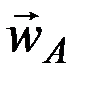на оси геоцентрической прямоугольной небесной (звездной) системы координат, которая в нашем случае оказывается наиболее удобной для аналитических расчетов.

Скорость вращения атмосферы в выбранной системе координат определяется степенью ее увлечения вращающейся Землей, причем в настоящее время принято считать, что атмосфера полностью увлекается вращающейся Землей, т.е. вращается вместе с ней с той же скоростью. По этой причине примем, что угловая скорость вращения атмосферы равна угловой скорости вращения Земли ω, а сам вектор линейной скорости вращения атмосферы 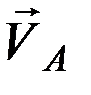лежит в плоскости параллельной плоскости земного экватора и по модулю равен 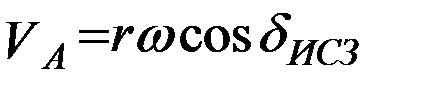, где r – геоцентрический радиус-вектор ИСЗ, а 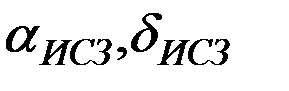его экваториальные координаты в НСК: прямое восхождение и склонение. Нетрудно видеть, что тогда вектор линейной скорости вращения атмосферы имеет вид:

.

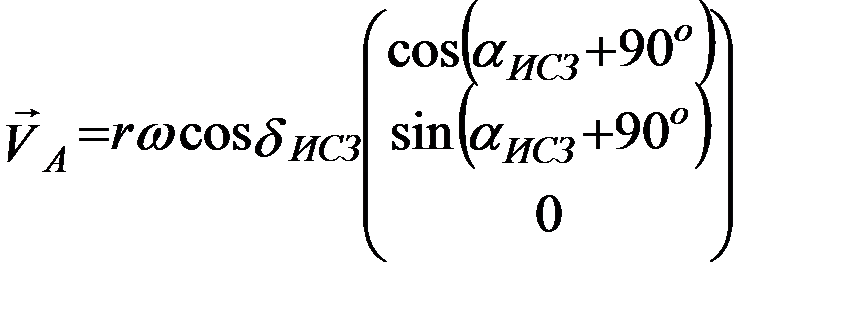Вектор линейной скорости спутника 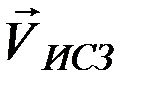складывается с вектором линейной скорости вращения атмосферы 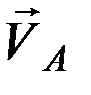по правилу параллелограмма:

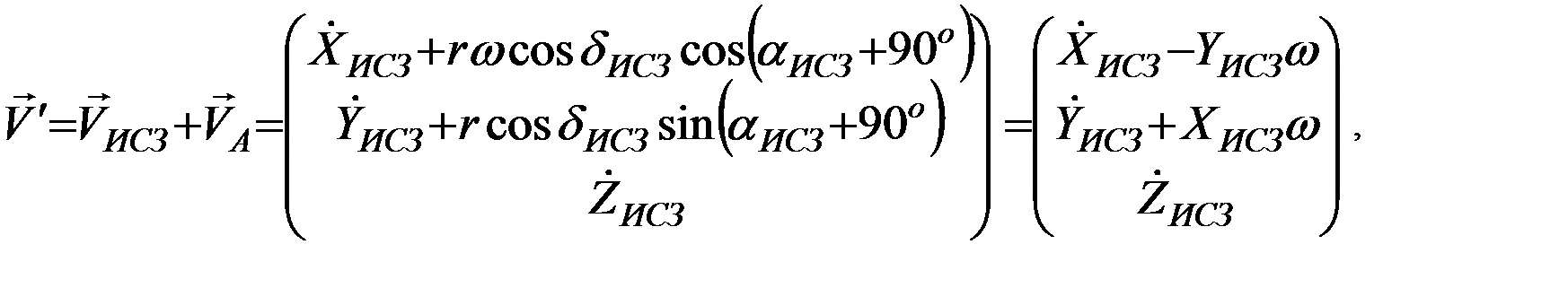
где 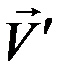, по-прежнему, вектор линейной скорости ИСЗ относительно атмосферы, позволяющий далее вычислить компоненты вектора силы атмосферного торможения: 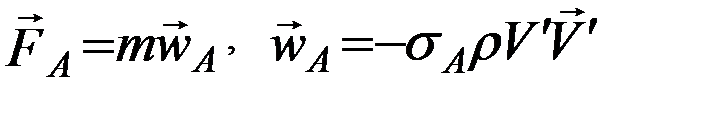, необходимого для дальнейшего интегрирования уравнений движения в прямоугольных координатах. Если уравнения движения записаны в форме уравнений Ньютона, необходимо путем трех элементарных вращений привести компоненты вектора 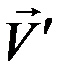в орбитальную спутникоцентрическую систему координат .

В данном параграфе нами рассмотрены все основные источники возмущений, которые необходимо учитывать при составлении дифференциальных уравнений возмущенного движения, вне зависимости, используем ли мы прямоугольные геоцентрические НСК, орбитальные спутникоцентрические системы координат (уравнения Ньютона) или соответствующие пертурбационные функции (уравнения Лагранжа). Важно заметить, воздействие тех или иных возмущающих факторов зависит как от параметров орбиты и предполагаемой продолжительности интервала интегрирования уравнений движения, так и от физических и геометрических характеристик самого спутника. Наиболее сложным учет возмущений оказывается в случае вытянутых орбит с большими эксцентриситетами и высотами апогеев.