Расчеты на прочность и жесткость статически определимых брусьев при растяжении – сжатии.
Сопротивление материалов
Контрольные задания
для студентов заочной формы обучения
Миасс 2017
Перечень вопросов по дисциплине
Вопросы к зачету
Сопротивление материалов
1. Сопротивление материалов. Основные положения.
2. Классификация нагрузок в сопротивлении материалов.
3. Допущения о свойствах материалов, принимаемые в сопротивлении материалов.
4. Допущения о характере деформирования элементов конструкций, принимаемые в сопротивлении материалов.
5. Метод сечений.
6. Виды нагружений бруса.
7. Напряжения.
8. Растяжение и сжатие.
9. Перемещения и деформации при растяжении (сжатии).
10. Закон Гука при растяжении.
11. Статические испытания материалов.
12. Основные механические характеристики материалов.
13. Расчеты на прочность при растяжении.
14. Практические расчеты на срез и смятие.
15. Геометрические характеристики плоских сечений.
16. Изгиб прямого бруса.
17. Построение эпюр поперечных сил и изгибающих моментов.
18. Расчеты на прочность при изгибе для пластичных материалов.
19. Расчеты на прочность при изгибе для хрупких материалов
20. Кручение. Построение эпюр.
21. Кручение круглого прямого бруса.
22. Расчет на прочность при кручении.
23. Расчет жесткость при кручении.
24. Напряженное состояние в точке тела.
25. Гипотезы прочности.
26. Расчеты бруса круглого поперечного сечения при изгибе с кручением.
Контрольная работа
Контрольная работа состоит из 3-х задач. Номер задания соответствует порядковому номеру студента в зачетно-экзаменационной ведомости группы.
Контрольная работа выполняется на листах формата А4. Примерное содержание контрольной работы:
· Титульный лист;
· Аннотация;
· Оглавление;
· Задача №1;
· Задача №2;
· Задача №3;
· Список литературы.
Контрольная работа должна быть оформлена в соответствии с требованиями стандарта организации СТО ЮУрГУ 04-2008. КУРСОВОЕ И ДИПЛОМНОЕ ПРОЕКТИРОВАНИЕ. ОБЩИЕ ТРЕБОВАНИЯ К СОДЕРЖАНИЮ И ОФОРМЛЕНИЮ.
В случае отсутствия у студента навыков работы на компьютере, возможно оформление контрольной работы в рукописной форме в отдельной ученической тетради.
Задача 1
Рассчитать моменты инерции сечения относительно центра тяжести заштрихованной части изображенной плоской.

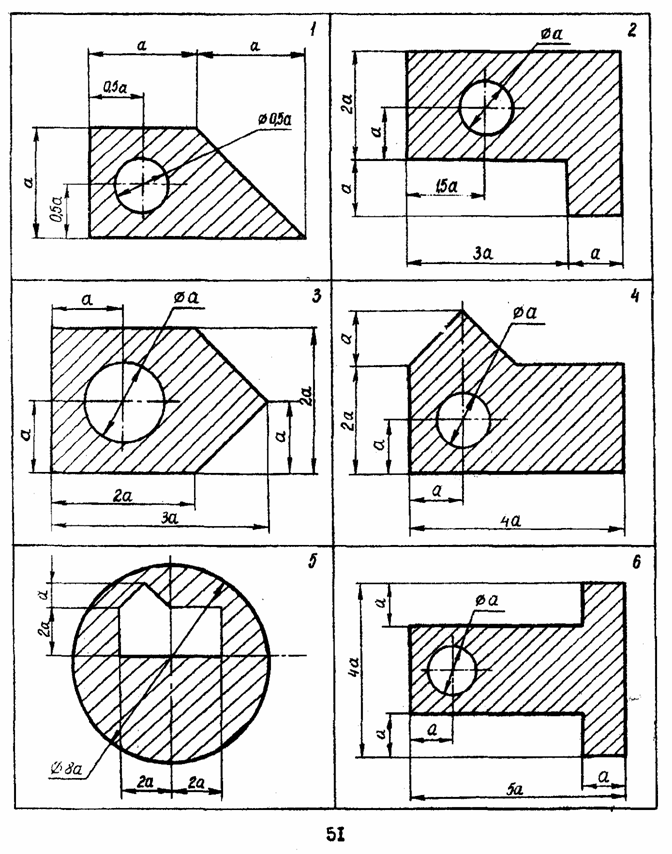
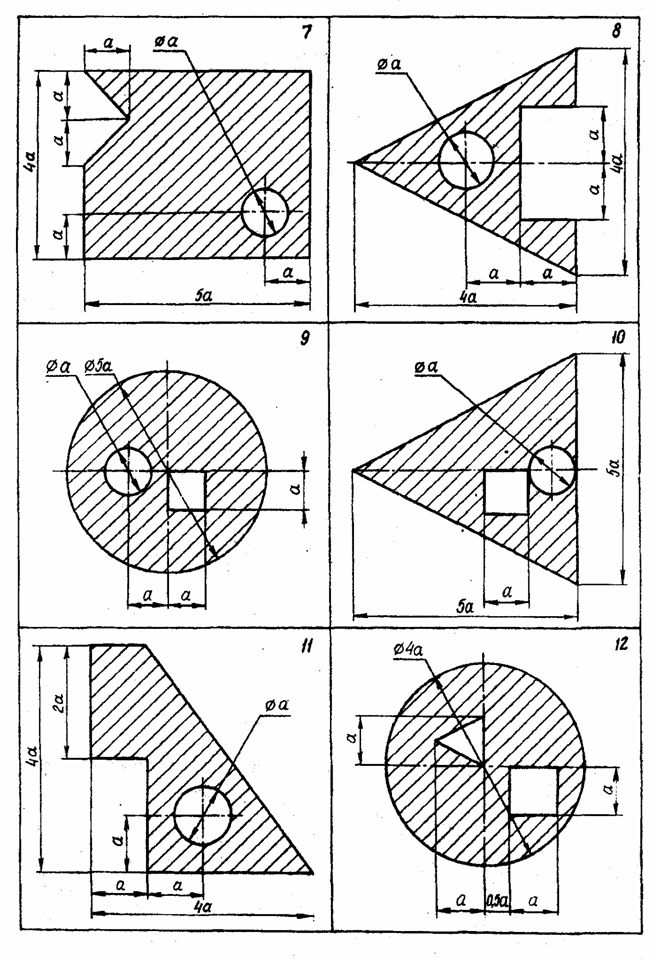

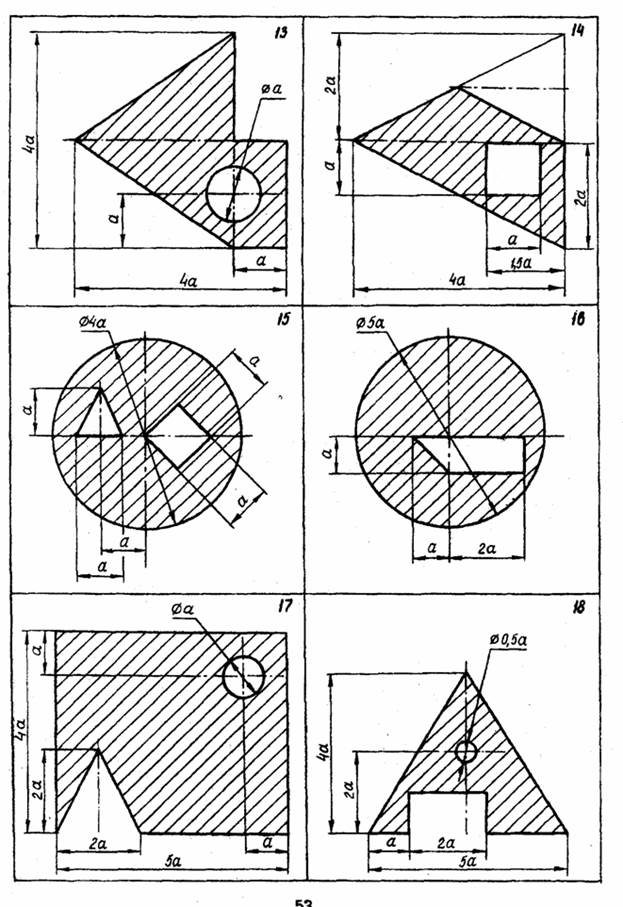



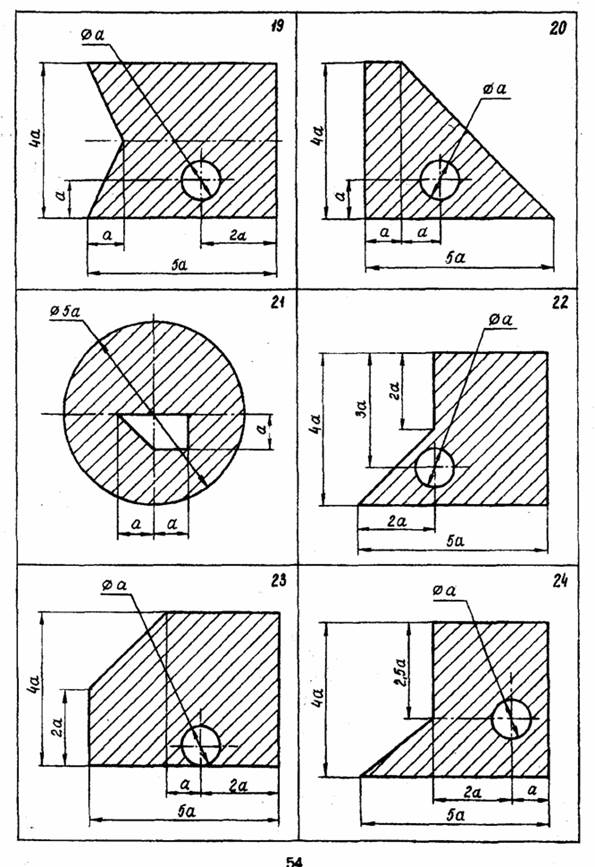

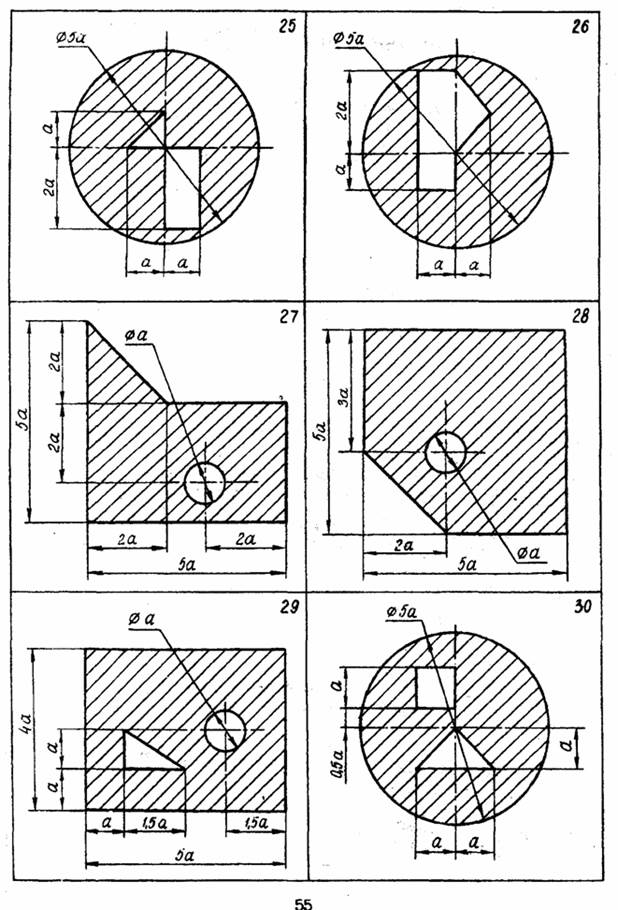
Таблица. Исходные данные к задаче
| № варианта | № схемы | а, см | № варианта | № схемы | а, см. | |
Задача 2
Расчеты на прочность и жесткость статически определимых брусьев при растяжении – сжатии.
Цель занятия: Научится строить графики продольных сил, напряжений и перемещений, а также проводить расчеты на прочность и жесткость.
Краткая теория.
Растяжением или сжатием называется такой вид деформации, при котором сечении бруса возникает только продольная сила т. е. направленная по оси стержня.
Стержнями называют тела, у которых один размер намного больше двух других.
Для построения эпюры продольных сил пользуются методом сечений.
Метод сечений заключается в том, что тело мысленно разрезается плоскостью на две части, любая из которых отбрасывается, и взамен нее к сечению оставшейся части прикладываются внутренние силы, действующие до разреза. Оставшаяся часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных на одну сторону сечения.
Растягивающие продольные силы считаются положительными, а сжимающие – отрицательными.
Для упрощения построения графика сил стержень необходимо разбить на участки. Участком называется отрезок оси стержня на протяжении которого график сил непрерывен.
Границами участка будем считать:
¾ Начало или конец стержня,
¾ Начало или конец распределенной нагрузки,
¾ Точка приложения сосредоточенной силы.
¾ Изменение размеров сечения.
Нумеровать участки следует со стороны свободного конца стержня или подвижного шарнира, т. к. в этих точках не возникает реакций.
Напряжение характеризует интенсивность внутренних сил, действующих в сечении. Размерность [Па]. При сжатии – растяжении в поперечном сечении возникают только нормальные напряжения, т. е. направленные перпендикулярно сечению, которые определяются по формуле:
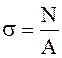 ,
,
где N – продольная сила в сечении,
А – площадь поперечного сечения.
При действии продольной силы стержень изменяет свою длину. Разница между конечной длиной и начальной называется абсолютным удлинением, которое можно найти по формуле:
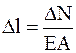 ,
,
где Е – модуль Юнга, являющийся характеристикой материала (для стали Е=2×1011Па)
l – длина рассматриваемого участка.
Произведение модуля Юнга на площадь сечения называется жесткостью сечения.
Пример.
Для данного ступенчатого бруса построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если Е=2×105 МПа=2×1011Па, F1=30кН=30×103Н, F2=38кН=38×103Н, F3=42кН=42×103Н, А1=1,9см2=1,9×10-4м2,
А2=3,1см2=3,1×10-4м2,[s]=160МПа.
Решение.
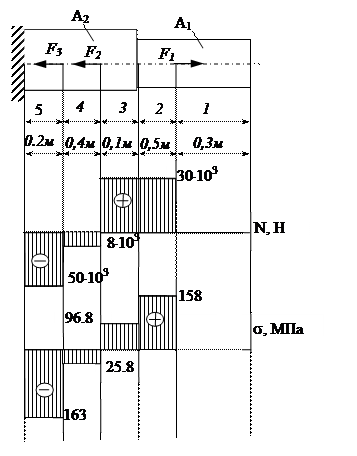
1. Разбиваем брус на участки как показано на рис.
2. Определяем ординаты эпюры N на участках бруса:
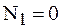 ,
, 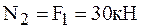 ,
, 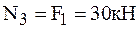 ,
, 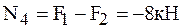 ,
,
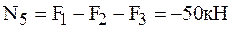 .
.
Строим эпюру продольных сил.
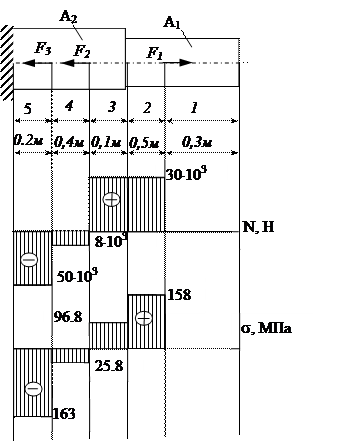
3. Вычисляем ординаты эпюры нормальных напряжений:
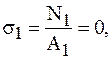
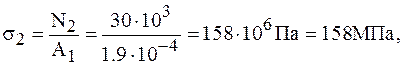
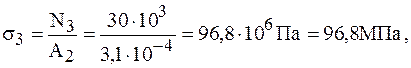
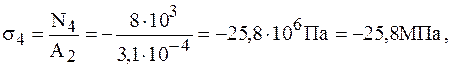
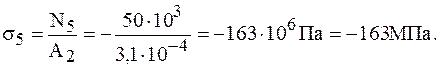
Строим эпюру нормальных напряжений.
Т. к. smax>s, то на прочность не выдержит.
 Определяем перемещение свободного конца:
Определяем перемещение свободного конца:
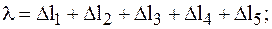
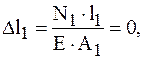
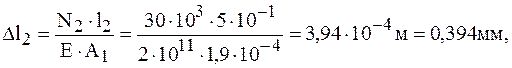
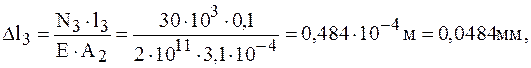
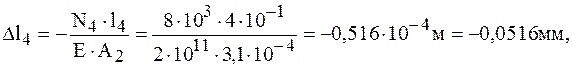
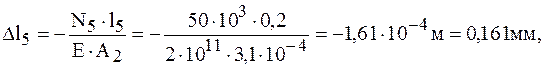
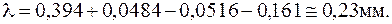
Брус удлиняется на 0,23 мм.
Вопросы для самопроверки.
1. Что такое сжатие – растяжение?
2. Что такое участок?
3. В каких опорах не возникают продольные силы?
4. Что такое напряжение?
5. Что такое нормальные напряжения и как они рассчитываются при сжатии – растяжении?
6. Что такое абсолютное удлинение?
7. Что характеризует модуль Юнга?
8. Что такое жесткость сечения при растяжении – сжатии?
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
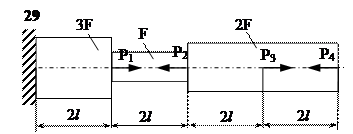 | 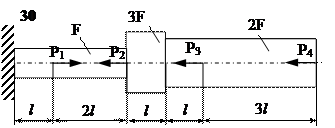 |
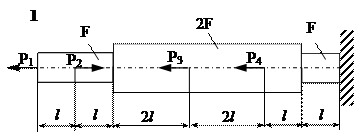
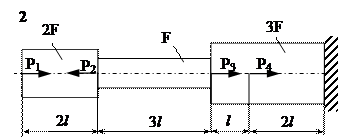
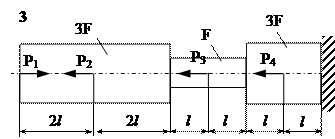
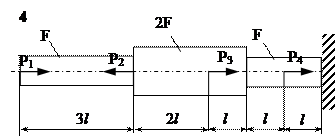
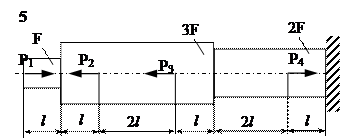
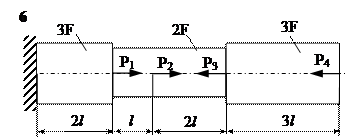
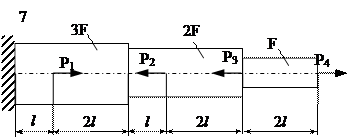
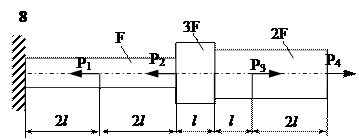
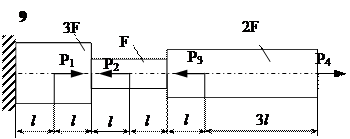
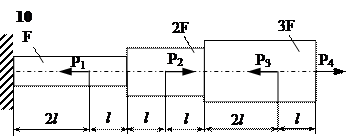
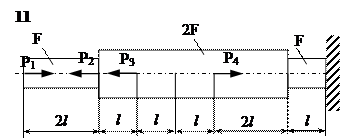
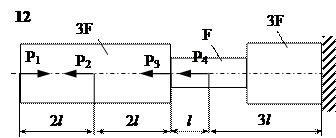
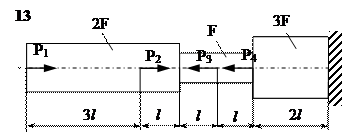
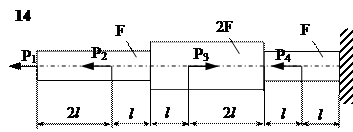
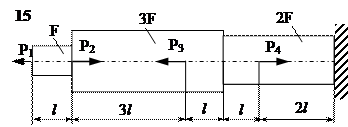
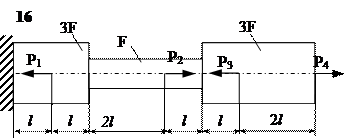
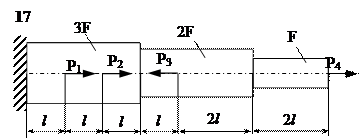
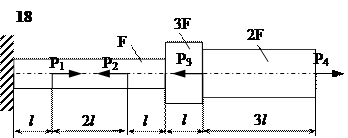
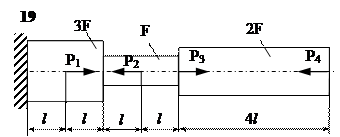
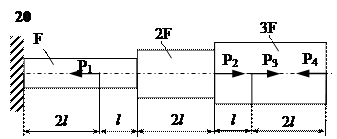
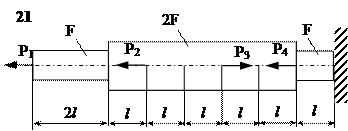
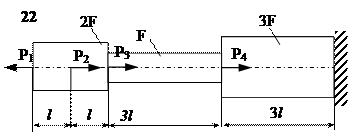
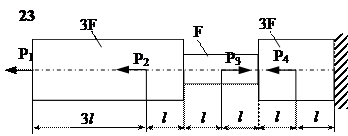
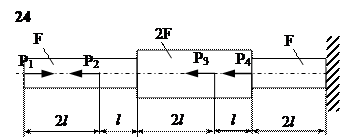
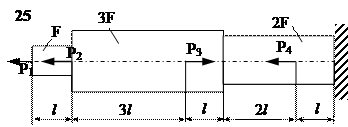
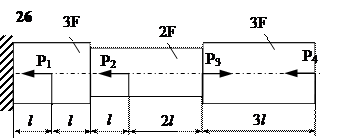
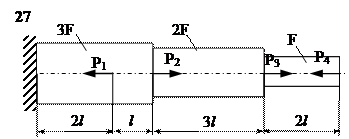
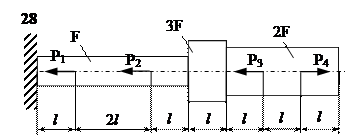
Задание
| № п/п | Р1, кН | Р2, кН | Р3, кН | Р4, кН | l, м | F,см2 |
| 0,1 | ||||||
| 0,2 | 2,1 | |||||
| 0,3 | 2,2 | |||||
| 0,4 | 2,3 | |||||
| 0,5 | 2,4 | |||||
| 0,6 | 2,5 | |||||
| 0,1 | 2,6 | |||||
| 0,2 | 2,7 | |||||
| 0,3 | 2,8 | |||||
| 0,4 | 2,9 | |||||
| 0,5 | ||||||
| 0,6 | ||||||
| 0,1 | 2,1 | |||||
| 0,2 | 2,2 | |||||
| 0,3 | 2,3 | |||||
| 0,4 | 2,4 | |||||
| 0,5 | 2,5 | |||||
| 0,6 | 2,6 | |||||
| 0,1 | 2,7 | |||||
| 0,2 | 2,8 | |||||
| 0,3 | 2,9 | |||||
| 0,4 | ||||||
| 0,5 | ||||||
| 0,6 | 2,1 | |||||
| 0,1 | 2,2 | |||||
| 0,2 | 2,3 | |||||
| 0,3 | 2,4 | |||||
| 0,4 | 2,5 | |||||
| 0,5 | 2,6 | |||||
| 0,6 | 2,7 |
Задача 3
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
К стальному валу постоянного поперечного сечения (рис. 3) приложены четыре внешних скручивающих момента: 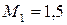 кН·м;
кН·м; 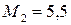 кН·м;
кН·м; 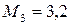 кН·м;
кН·м; 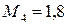 кН·м. Длины участков стержня:
кН·м. Длины участков стержня: 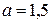 м;
м; 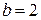 м,
м, 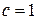 м,
м, 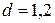 м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при
м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при 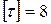 кН/см2 =80 МПа, и построить эпюру углов закручивания поперечных сечений стержня.
кН/см2 =80 МПа, и построить эпюру углов закручивания поперечных сечений стержня.
Сопротивление материалов
Контрольные задания
для студентов заочной формы обучения
Миасс 2017
Перечень вопросов по дисциплине
Вопросы к зачету
Сопротивление материалов
1. Сопротивление материалов. Основные положения.
2. Классификация нагрузок в сопротивлении материалов.
3. Допущения о свойствах материалов, принимаемые в сопротивлении материалов.
4. Допущения о характере деформирования элементов конструкций, принимаемые в сопротивлении материалов.
5. Метод сечений.
6. Виды нагружений бруса.
7. Напряжения.
8. Растяжение и сжатие.
9. Перемещения и деформации при растяжении (сжатии).
10. Закон Гука при растяжении.
11. Статические испытания материалов.
12. Основные механические характеристики материалов.
13. Расчеты на прочность при растяжении.
14. Практические расчеты на срез и смятие.
15. Геометрические характеристики плоских сечений.
16. Изгиб прямого бруса.
17. Построение эпюр поперечных сил и изгибающих моментов.
18. Расчеты на прочность при изгибе для пластичных материалов.
19. Расчеты на прочность при изгибе для хрупких материалов
20. Кручение. Построение эпюр.
21. Кручение круглого прямого бруса.
22. Расчет на прочность при кручении.
23. Расчет жесткость при кручении.
24. Напряженное состояние в точке тела.
25. Гипотезы прочности.
26. Расчеты бруса круглого поперечного сечения при изгибе с кручением.
Контрольная работа
Контрольная работа состоит из 3-х задач. Номер задания соответствует порядковому номеру студента в зачетно-экзаменационной ведомости группы.
Контрольная работа выполняется на листах формата А4. Примерное содержание контрольной работы:
· Титульный лист;
· Аннотация;
· Оглавление;
· Задача №1;
· Задача №2;
· Задача №3;
· Список литературы.
Контрольная работа должна быть оформлена в соответствии с требованиями стандарта организации СТО ЮУрГУ 04-2008. КУРСОВОЕ И ДИПЛОМНОЕ ПРОЕКТИРОВАНИЕ. ОБЩИЕ ТРЕБОВАНИЯ К СОДЕРЖАНИЮ И ОФОРМЛЕНИЮ.
В случае отсутствия у студента навыков работы на компьютере, возможно оформление контрольной работы в рукописной форме в отдельной ученической тетради.
Задача 1
Рассчитать моменты инерции сечения относительно центра тяжести заштрихованной части изображенной плоской.











Таблица. Исходные данные к задаче
| № варианта | № схемы | а, см | № варианта | № схемы | а, см. | |
Задача 2
Расчеты на прочность и жесткость статически определимых брусьев при растяжении – сжатии.
Цель занятия: Научится строить графики продольных сил, напряжений и перемещений, а также проводить расчеты на прочность и жесткость.
Краткая теория.
Растяжением или сжатием называется такой вид деформации, при котором сечении бруса возникает только продольная сила т. е. направленная по оси стержня.
Стержнями называют тела, у которых один размер намного больше двух других.
Для построения эпюры продольных сил пользуются методом сечений.
Метод сечений заключается в том, что тело мысленно разрезается плоскостью на две части, любая из которых отбрасывается, и взамен нее к сечению оставшейся части прикладываются внутренние силы, действующие до разреза. Оставшаяся часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных на одну сторону сечения.
Растягивающие продольные силы считаются положительными, а сжимающие – отрицательными.
Для упрощения построения графика сил стержень необходимо разбить на участки. Участком называется отрезок оси стержня на протяжении которого график сил непрерывен.
Границами участка будем считать:
¾ Начало или конец стержня,
¾ Начало или конец распределенной нагрузки,
¾ Точка приложения сосредоточенной силы.
¾ Изменение размеров сечения.
Нумеровать участки следует со стороны свободного конца стержня или подвижного шарнира, т. к. в этих точках не возникает реакций.
Напряжение характеризует интенсивность внутренних сил, действующих в сечении. Размерность [Па]. При сжатии – растяжении в поперечном сечении возникают только нормальные напряжения, т. е. направленные перпендикулярно сечению, которые определяются по формуле:
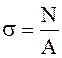 ,
,
где N – продольная сила в сечении,
А – площадь поперечного сечения.
При действии продольной силы стержень изменяет свою длину. Разница между конечной длиной и начальной называется абсолютным удлинением, которое можно найти по формуле:
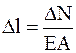 ,
,
где Е – модуль Юнга, являющийся характеристикой материала (для стали Е=2×1011Па)
l – длина рассматриваемого участка.
Произведение модуля Юнга на площадь сечения называется жесткостью сечения.
Пример.
Для данного ступенчатого бруса построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если Е=2×105 МПа=2×1011Па, F1=30кН=30×103Н, F2=38кН=38×103Н, F3=42кН=42×103Н, А1=1,9см2=1,9×10-4м2,
А2=3,1см2=3,1×10-4м2,[s]=160МПа.
Решение.
1. Разбиваем брус на участки как показано на рис.
2. Определяем ординаты эпюры N на участках бруса:
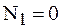 ,
, 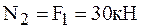 ,
, 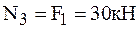 ,
, 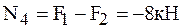 ,
,
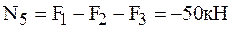 .
.
Строим эпюру продольных сил.

3. Вычисляем ординаты эпюры нормальных напряжений:
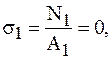
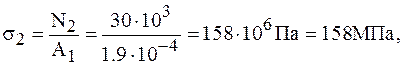
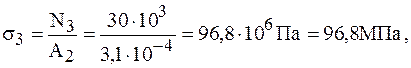
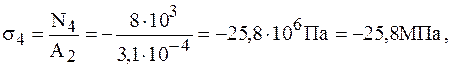
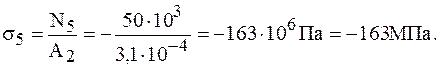
Строим эпюру нормальных напряжений.
Т. к. smax>s, то на прочность не выдержит.
 Определяем перемещение свободного конца:
Определяем перемещение свободного конца:
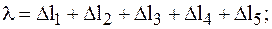
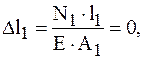
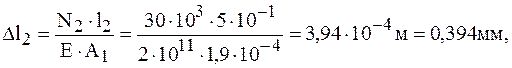
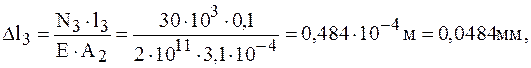
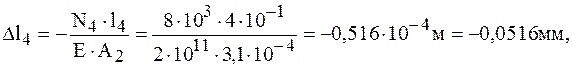
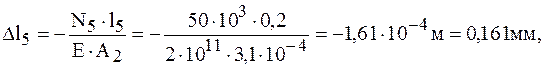
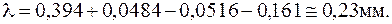
Брус удлиняется на 0,23 мм.
Вопросы для самопроверки.
1. Что такое сжатие – растяжение?
2. Что такое участок?
3. В каких опорах не возникают продольные силы?
4. Что такое напряжение?
5. Что такое нормальные напряжения и как они рассчитываются при сжатии – растяжении?
6. Что такое абсолютное удлинение?
7. Что характеризует модуль Юнга?
8. Что такое жесткость сечения при растяжении – сжатии?
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Задание
| № п/п | Р1, кН | Р2, кН | Р3, кН | Р4, кН | l, м | F,см2 |
| 0,1 | ||||||
| 0,2 | 2,1 | |||||
| 0,3 | 2,2 | |||||
| 0,4 | 2,3 | |||||
| 0,5 | 2,4 | |||||
| 0,6 | 2,5 | |||||
| 0,1 | 2,6 | |||||
| 0,2 | 2,7 | |||||
| 0,3 | 2,8 | |||||
| 0,4 | 2,9 | |||||
| 0,5 | ||||||
| 0,6 | ||||||
| 0,1 | 2,1 | |||||
| 0,2 | 2,2 | |||||
| 0,3 | 2,3 | |||||
| 0,4 | 2,4 | |||||
| 0,5 | 2,5 | |||||
| 0,6 | 2,6 | |||||
| 0,1 | 2,7 | |||||
| 0,2 | 2,8 | |||||
| 0,3 | 2,9 | |||||
| 0,4 | ||||||
| 0,5 | ||||||
| 0,6 | 2,1 | |||||
| 0,1 | 2,2 | |||||
| 0,2 | 2,3 | |||||
| 0,3 | 2,4 | |||||
| 0,4 | 2,5 | |||||
| 0,5 | 2,6 | |||||
| 0,6 | 2,7 |
Задача 3
