Концепция криптосистемы с открытым ключом
Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования - другой ключ (отсюда и название - асимметричные). Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно.
Для расшифрования данных получатель зашифрованной информации использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.
Обобщенная схема асимметричной криптосистемы с открытым ключом показана на рис.1. В этой криптосистеме применяют два различных ключа: КА - открытый ключ отправителя A; КВ -секретный ключ получателя В. Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ КА по незащищенному каналу). Значения ключей КА и КВ зависят от начального состояния генератора ключей.
Раскрытие секретного ключа КВ по известному открытому ключу КА должно быть вычислительно неразрешимой задачей.
Характерные особенности асимметричных криптосистем:
1. Открытый ключ КА и криптограмма С могут быть отправлены по незащищенным каналам, т.е. противнику известны КВ и С.
2. Алгоритмы шифрования и расшифрования
ЕВ: М ® С,
DВ: C ® M,
являются открытыми.
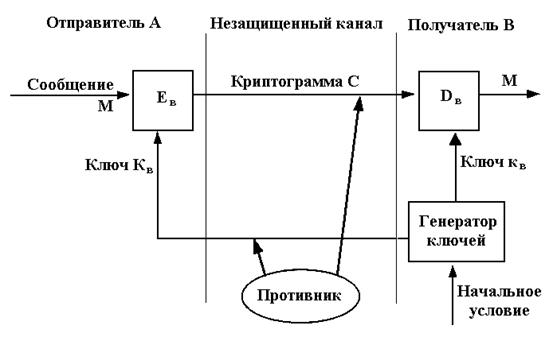
Рис.1. Обобщенная схема асимметричной криптосистемы с открытым ключом
Защита информации в асимметричной криптосистеме основана на секретности ключа КВ.
У.Диффи и М.Хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:
1. Вычисление пары ключей (КА, КВ) получателем В на основе начального условия должно быть простым.
2. Отправитель А, зная открытый ключ КА и сообщение М, может легко вычислить криптограмму
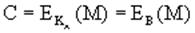 (1)
(1)
3. Получатель В, используя секретный ключ КВ и криптограмму С, может легко восстановить исходное сообщение
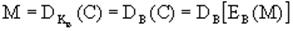 (2)
(2)
4. Противник, зная открытый ключ КА, при попытке вычислить секретный ключ КВ наталкивается на непреодолимую вычислительную проблему.
5. Противник, зная пару (КВ, С), при попытке вычислить исходное сообщение М наталкивается на непреодолимую вычислительную проблему.
Алгоритм RSA
Следующий пример наглядно демонстрирует алгоритм шифрования RSA:
Зашифруем и расшифруем сообщение "САВ" по алгоритму RSA. Для простоты возьмем небольшие числа - это сократит наши расчеты.
- Выберем p=3 and q=11.
- Определим n= 3*11=33.
- Hайдем (p-1)*(q-1)=20. Следовательно, d будет равно, например, 3: (d=3).
- Выберем число е по следующей формуле: (e*3) mod 20=1. Значит е будет равно, например, 7: (e=7).
- Представим шифруемое сообщение как последовательность чисел в диапозоне от 0 до 32 (незабывайте, что кончается на n-1). Буква А =1, В=2, С=3.
Теперь зашифруем сообщение, используя открытый ключ {7,33}
C1 = (3^7) mod 33 = 2187 mod 33 = 9;
C2 = (1^7) mod 33 = 1 mod 33 = 1;
C3 = (2^7) mod 33 = 128 mod 33 = 29;
Теперь расшифруем данные, используя закрытый ключ {3,33}.
M1=(9^3) mod 33 =729 mod 33 = 3(С);
M2=(1^3) mod 33 =1 mod 33 = 1(А);
M3=(29^3) mod 33 = 24389 mod 33 = 2(В);
Данные расшифрованы!
Билет
