Метод визуально-графической поддержки решения задач на проценты.

Автором метода визуально-графической поддержки решения задач на проценты является преподаватель кафедры математики КПТУ - Марина Юрьевна Коваленко. Условия подавляющего большинства задач на смешивание растворов веществ, примесей, выпариваний может быть представлено в следующем виде:

Прямоугольники символизируют некоторый раствор, сплав веществ, смесь,

+ подразумевает смешивание растворов, добавление вещества, сплавление и т.д.

- показывает удаление примеси, выпаривание, удаление части смеси.

= показывает, что в результате получено новое вещество.

А_1, А₂ -масса или объем первой или второй смеси.

Р₁ %- процентное содержание некоторого чистого вещества в смеси А₁.

Р₂ %- процентное содержание некоторого чистого вещества в смеси А₂.

А₁ + или – А₂ - масса или объем полученной смеси в результате смешивания

(+) или удаления (-) смеси 1 или 2.

Р % процентное содержание чистого вещества в новой смеси.

Задачи на смеси, растворы, сплавы.

Данный тип задач охватывает большой круг ситуаций - смешивание товаров различной цены, жидкостей с различным содержанием соли, кислот различной концентрации, сплавлении металлов с различным содержанием некоторого металла и прочее.

При решении задач данного типа используются следующие допущения:

_1. Всегда выполняется «Закон сохранения объема или массы» если два раствора или сплава соединяют в «новый» раствор или сплав, то выполняются равенства у = у₁ + у₂ -сохраняется объем Закон сохранения массы – m = m₁ + m₂

2. Данный закон выполняется и для отдельных составляющих частей (компонентов) сплава (раствора).

3. При соединении растворов и сплавов не учитываются химические взаимодействия их отдельных компонентов.

Задачи на смеси, растворы и сплавы называют еще задачами на процентное содержание или концентрацию. Говоря о смесях, растворах и сплавах употребляется термин «смесь» независимо от ее вида (твердая, жидкая, газообразная, сыпучая и т. д). Смесь состоит из чистого вещества и примеси

Решение задач

1. Морская вода содержит 5 % по весу соли. Сколько кг пресной воды нужно прибавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2 %?

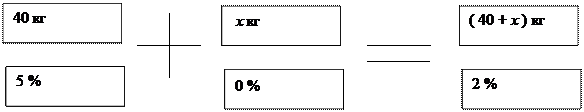
40 * 5 + 0 * х = (40 + х) * 2

х = 60

Ответ:60кг.

1. Имеется лом стали двух сортов с содержанием никеля 5% и40 %. Сколью

Нужно взять каждого из этих сортов , чтобы получить 140 т стали с

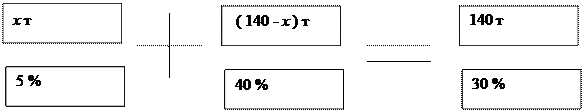содержанием никеля в 30 %?

х * 5 + 40 (140 - х) = 140 * 30

5х + 5 600 – 40 х = 4 200

- 35 х = - 1400

х = 40

Ответ: 40 и 100т.

1. Кусок сплава меди с оловом весом 12кг содержит 45% меди. Сколько чистого олова надо прибавить к этому куску , чтобы получившийся новый сплав имел 40 % меди?

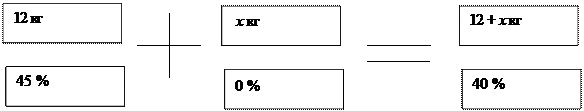
12 * 45 + х * 0 = 40 ( 12 + х )

540 = 480 + 40 х

х = 1,5

Ответ: 1,5 чистого олова надо добавить

4. Сколько чистого спирта надо прибавить к 735 г. 16% раствора йода в спирте, чтобы получился 10% раствор?

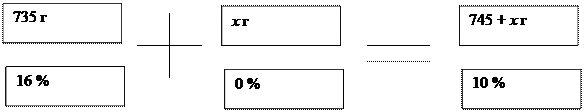
735 * 16 + х * 0 = ( 735 + х ) * 10

х = 441

Ответ: 441г.

1. Древесина только что срубленного дерева содержит 64% воды. Через неделю количество воды стало 48% от веса дерева. Насколько уменьшился при этом вес дерева, если только что срубленное дерево весило 7,5 ц. Ответ округлить до десятых.

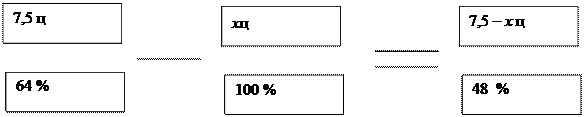
7,5 * 64 – 100 х = ( 7,5 – х ) * 48

Ответ: приблизительно 2,3ц.

1. Из 20 т руды выплавлено 8 т металла, содержащего 5% примеси. Каков процент примеси в руде?

10 * х – 1 200 = 40

20 х = 1 240

х = 6 2

Ответ: 62т.

1. Если смешать 8 кг. и 2 кг. серной кислоты разной концентрации, то получится раствор 12% кислоты. При смешивании двух одинаковых масс тех же растворов получили 15% раствор. Определить первоначальную концентрацию растворов.

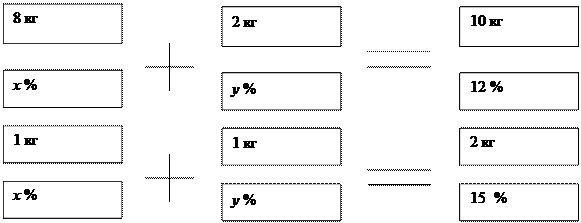
Составляем систему уравнений:

8 х + 2 у = 120

х + у = 30

Ответ: 10% и 20%.

1. Сколько воды нужно выпарить из 0,5 т. целлюлозной массы, содержащей 85 % воды, чтобы получить массу с содержанием 75 % воды?

0,5 * 85 -100 х = 75 ( 0,5 – х )

х = 0.2 т.

Ответ: 0,2 т.

1. Из руды, содержащей 25% примесей после переплавки получили 30 т металла. Сколько % примесей содержит, полученный металл ?

38 * 25 – 8 * 100 = 30 х

Ответ: 5 %.

1. Пчелы, перерабатывая цветочный нектар в мед освобождают его от значительной массы воды. Исследования показали, что нектар содержит 70 % воды, а полученный мед 17% воды. Сколько килограммов нектара приходится перерабатывать пчелам для получения 1 кг. меда?

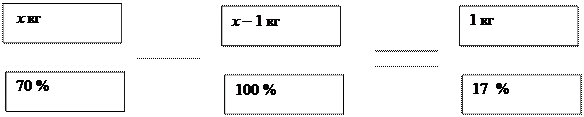
70 х - ( х – 1 ) * 100 = 1 7

70 х – 100 х + 100 = 17

- 30 х = - 93

х = 3

Ответ: приблизительно З кг.

1. На складе есть 100кг. ягод. Проведенный анализ показал, что в ягодах содержится 99% воды. Через некоторое время анализ повторили. Оказалось что, содержание воды в ягодах упало до 98%. Какова теперь масса ягод?

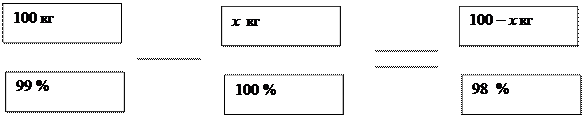
99 * 100 – 100 х = 98 ( 100 – х )

9 900 – 100 х = 9 800 – 98 х

- 100 х + 98 х = 9 800 – 9 900

- 2 х = - 100

х = 50

Ответ: 50 кг ягод

1. В банке находится 40 литров 40 % раствора сахарного песка. Сколько воды надо добавить, чтобы в растворе было 20 %песка?

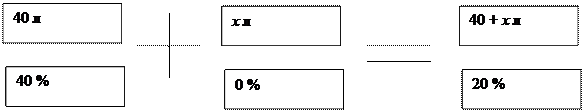
40 * 40 = 20 ( 40 + х )

1 600 = 800 + 20 х

1 600 – 800 = 20 х

800 = 20 х

х = 40

Ответ: 40 л.