Элементы погруженного объема судна при посадке его прямо, но с дифферентом

Наличие дифферента заметно влияет на характеристики отдельных элементов погруженного объема корпуса судна. Определение их при наличии дифферента по кривым элементам теоретического чертежа исключено, так как приведет к большим погрешностям. Такие характеристики, как величина погруженного объема и координаты ЦВ судна в случае посадки с дифферентом требуют своих способов расчетов.

3.5.1. Масштаб Бонжана. Для определения водоизмещения и абсциссы х_с судна с дифферентом используется масштаб Бонжана (рис.24), представляющий собой совокупность интегральных кривых погруженных площадей шпангоутов (рис.17). Кривые ω_i(d) строятся при следах соответствующих шпангоутов на чертеже диаметрального сечения корпуса судна. Для удобства пользования масштаб чертежа по высоте берется в несколько раз крупнее, чем по длине, а масштаб абсцисс кривых ω_i(d) принимают соответствующим точности расчета площади ω. При использовании масштаба Бонжана вычерчивают на нем след наклонной ватерлинии по известным осадкам d_н и d_к, и отмечают точки ее пересечения с перпендикулярами, соответствующим положению шпангоутов. Площади шпангоутов ω_i снимаются по горизонтали и представляют собой расстояния от ватерлинии до соответствующей интегральной кривой.

Полученные величины подставляют в расчетные формулы, полученные по правилам приближенного интегрирования (правило трапеций):

V = 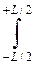ω dx @ dL [ω ₀ + ω₁ + ω₂ + … + ω_n – 1/2(ω ₀ + ω_n)];

,

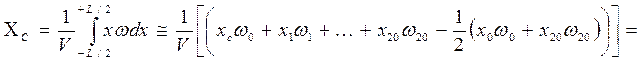
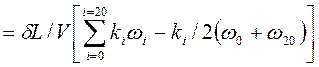где dL = L / 20 - длина теоретической шпации; k_i - множители отстояния шпангоутов от плоскости миделя в теоретических шпациях. Расчет рекомендуется выполнять в табличной форме (табл. 2).

Номера теоретических шпангоутов	Множители плеч, ki	Погруженные площади шпангоутов, ωi (м2)	ki ωi (м2)
I	II	III	IV
… …	… - 1 … - 8 - 9 -10
Сумма S/
Поправка ε
Исправленная сумма S=S¢ - ε
dL = L / 20, м	V = dL S·III + dV, м3	Хс = (dL SIV + dМ) /(SIII +dV), м

Таблица 2.

Масштаб Бонжана строится, как правило, по данным теоретического чертежа и не учитывает объемы выступающих частей (рули, винты, кронштейны, гребные валы, толщина обшивки корпуса и др.). Следовательно, для определения действительных значений V и x_с в расчетные результаты следует ввести поправки на объем выступающих частей dV и их моментов относительно плоскости мидель-шпангоута dМ.

При пользовании масштабом Бонжана не следует допускать две возможные ошибки. Во-первых, в связи с различием линейных масштабов чертежа по длине и высоте нельзя наносить след ватерлинии непосредственно по заданной величине угла дифферента. Во-вторых, изменение абсцисс кривых ω_i(d) недопустимо производить по точкам пересечения следа ватерлинии с самими кривыми. Их следует отсчитывать от пересечения следа ватерлинии со следом соответствующих шпангоутов.

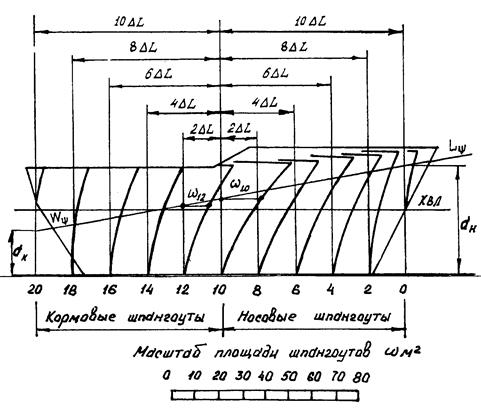Рис.24. Масштаб Бонжана

3.5.2. Дифферентные диаграммы.Для судовых условий выполнение расчетов по определению элементов погруженного объема судна с помощью масштаба Бонжана требует сравнительно много времени. С достаточной для практики точностью эти элементы могут быть непосредственно определены при помощи специальных диаграмм, получивших название дифферентных (рис. 25). Широкое распространение получили диаграммы Г.А.Фирсова (рис.25, а), Петерсена, КТИРПиХ (рис.25,б) и диаграмма посадок (рис.25, в).

На диаграмме Г.А.Фирсова в прямоугольной системе кординат представлены зависимости между водоизмещением судна, абсциссами ЦВ и отвечающими им осадками носом и кормой. Цифры, стоящие на кривых, показывают, к каким значениям водоизмещения и абсциссы ЦВ относится данная кривая.

Отличаются друг от друга эти диаграммы только формой представления элементов погруженного объема и позволяют определить массу судна Δ и абсциссы ЦТ (ЦВ) x_c » x_g.

Основное достоинство дифферентных диаграмм в том, что они позволяют непосредственно определить элементы погруженного объема судна по известным параметрам посадки.

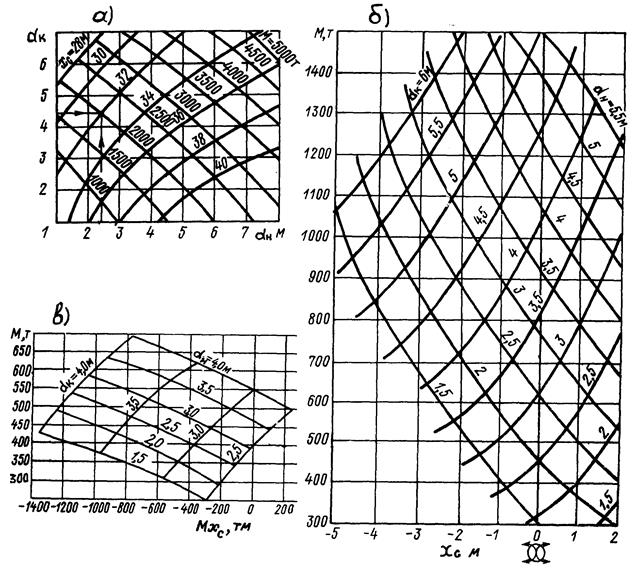
Рис.25. Дифферентные диаграммы

Глава 4

Плавучесть судна

Условие плавучести судна

Плавучестью называется способность судна плавать в состоянии равновесия в заданном положении относительно поверхности воды при заданной нагрузке.

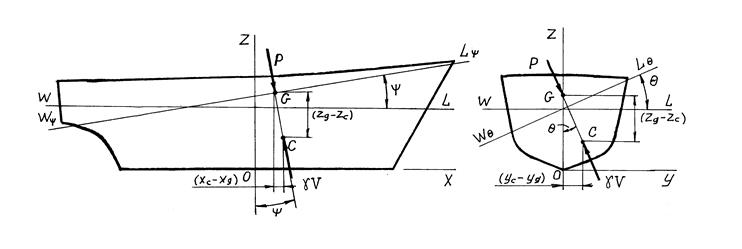
На судно, плавающее без хода на спокойной воде, действуют две категории сил: силы тяжести и силы избыточных гидростатических давлений (рис.26). Силы тяжести представляют собой силы тяжести корпуса, механизмов, систем и устройств, запасов, экипажа и др. Силы тяжести приводятся к одной равнодействующей - силе тяжести судна Р, которая направлена вертикально вниз и приложена в центре тяжести судна(ЦТ) - в точке G с координатами x_g , y_g , z_g .

Рис. 26. К составлению уравнений равновесия плавающего судна

Силы избыточных гидростатических давлений, действующие на поверхность погруженной части корпуса судна, также приводятся к одной равнодействующей – гидростатической силе поддержания (силе плавучести).

Сила плавучести направлена вертикально вверх и приложена в центре величины судна (ЦВ) - в точке С с координатами x_с, y_с, z_с. Центр величины представляет собой геометрический центр подводного объема судна V и его положение зависит от формы корпуса судна и его посадки.

Условия равновесия плавающего судна:

1.Сила тяжести (масса) судна равна весу (массе) вытесненной им воды:

Р = γV; Δ = ρV.

где V- объемное водоизмещение судна м³,

γ - удельный вес воды (.γ = 10,05 кН/м³- для морской и γ = 9,81 кН/м³ - для пресной воды),

ρ - плотность воды (ρ = 1,025 т/м³- для морской и ρ = 1,0 т/м³- для пресной воды).

2.Центр тяжести (ЦТ) и центр величины (ЦВ) судна лежат на одной вертикали, перпендикулярной к плоскости ватерлинии (рис.26);

(x_с - x_g) + (z_c – z_g) tg Y = 0;

(y_с - y_g) + (z_c – z_g) tg Q = 0,

где x_с, y_с и z_c – координаты центра величины судна;

x_g ,y_g и z_g – координаты центра тяжести судна.

Если судно сидит прямо и на ровный киль (Y = Q = 0), то уравнение принимает вид:

x_g = x_с; y_g = y_с.

В практических расчетах судна, плавающего с дифферентом, часто пренебрегают величиной (z_c – z_g) tg Y по сравнению x_с, т.е. полагают, что x_с ≈ x_g. Принятое допущение дает незначительную ошибку при определении элементов плавучести судна.