Устройство судна и движители

Глава 2

Основы гидромеханики

Основные свойства жидкостей

Гидромеханикой называется наука о равновесии и движении жидкости и о взаимодействии жидкости с твердыми телами.

Гидромеханика, представляя собой, раздел общей механики, подразделяется на гидростатику и гидродинамику.

В гидростатике изучаются жидкости в состоянии покоя, в гидродинамике - в состоянии движения.

В гидродинамике рассматриваются тела, характеризующиеся легкой подвижностью (текучестью). Тела, обладающие текучестью, способны, не дробясь на части, изменять свою форму при действии незначительных усилий. Такие тела называются жидкостями.

Под жидкостью в гидромеханике понимают жидкие и газообразные среды, так как им присущи общие свойства, а наблюдающиеся явления можно описать одинаковыми зависимостями. Однако между капельными жидкостями и газами имеются отличия:

Капельные жидкости	Газообразные среды
1.Значительные силы межмолекулярного взаимодействия образуют свободные поверхности. 2.Плохо сжимаются.	1.Силы межмолекулярного взаимодействия отсутствуют, поэтому свободные поверхности не образуются, а полностью занимают объем, в котором они находятся. 2. Хорошо сжимаются.

Основными механическими свойствами жидкости являются:

Весомость жидкости характеризующейся удельным весом - отношением веса жидкости р к занимаемому объему v

γ = р/v.

Плотность жидкости - отношение массы жидкости m к ее объему v

ρ = m/v.

Плотность и удельный вес связаны между собой зависимостями γ = ρg, где g = 9,81 м/с² - ускорение свободного падения. В судовых расчетах принимают:

для пресной воды ρ = 1,0 т/м³ (102 кгс·с²/м⁴), γ = 9,81 кН/м³;

для морской воды стандартной плотности ρ = 1,025 т/м³, (105 кгс·с²/м⁴), γ = 10,06 кН/м³;

для воздуха ρ = 1,225 кг/м³ (0,125 кгс·с²/м⁴), γ = 12,02 Н/м³.

Поверхностным натяжением называется свойство жидкости испытывать дополнительное давление на свободной поверхности под действием молекулярных сил сцепления. Это свойство жидкости характеризуется коэффициентом поверхностного натяжения α.

Вязкость – способность жидкости оказывать сопротивление при скольжении одной ее части относительно другой. Сила внутреннего трения F пропорциональна изменению скорости жидкости υ в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости

F = μ·(dυ/dy)·S.

Это закон вязкого трения Ньютона. Коэффициент пропорциональности в нем называется коэффициентом динамической вязкости - μ (Па·с).

Отношение коэффициента динамической вязкости к плотности жидкости называется коэффициентом кинематической вязкости

ν = μ/ ρ.

Коэффициент кинематической вязкости зависит от температуры. При температуре 20⁰ С для воды он составляет 1·10^-6 м²/с, для воздуха - 1,5·10^-5 м²/с.

Гидростатика

Гидростатика изучает законы равновесия жидкой среды и взаимодействие жидкости с твердыми телами, т.е. в ситуациях, когда движение отсутствует или скорость пренебрежительно мала.

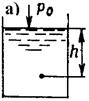
Гидростатика позволяет понять некоторые свойства такой важной гидродинамической величины, как давление. Давление твердого тела определяется его весом, давление жидкости - ее глубиной. Сила давления на дно сосуда р (рис.1,а) не зависит от его формы, а определяется только уровнем налитой в сосуд жидкости в соответствии с гидростатической формулой:

р = р₀ + ρgh;

р = р₀ + р_м ,

где ρ - плотность жидкости, р₀ - давление жидкости на некотором фиксированном уровне (при наличии свободной поверхности - атмосферное давление), h - отстояние по вертикали от этого уровня до рассматриваемой точки (глубина погружения), р_и - избыточное (манометрическое) давление.

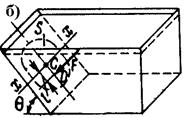
Соприкасаясь с твердым телом, жидкость оказывает на него давление, направленное по нормали к поверхности тела. Сила избыточного давления жидкости на плоскую поверхность, имеющую вертикальную ось симметрии (рис.1,б)

F = ρgh_cS,

где h_c - отстояние по вертикали ц.т. площади поверхности от уровня свободной поверхности жидкости; S - площадь поверхности.

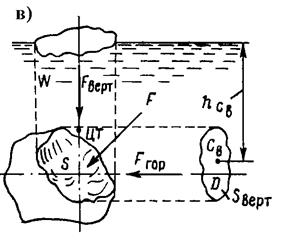Рис.1. Гидростатическое давление и сила давления жидкости.

Точка D приложения равнодействующей сил давления на поверхность называемая центром давления (ц.д.), отстоит от ц.т. площади (C) на расстоянии l.

Силу избыточного давления на криволинейную поверхность (рис.1,в) определяют ее составляющие F_x , F_y и F_z, по осям координат

F = .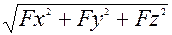

Горизонтальная составляющая силы давления на криволинейную поверхность (F_x или F_y )

F_гор = ρgh_cвS_верт,

где h_cв - отстояние по вертикали ц.т вертикальной проекции от плоскости гидростатического напора (рис. 1,в ).

Линия действия силы F_гор проходит через центр давления D площади вертикальной проекции S_верт.

Вертикальная составляющая силы давления на криволинейную поверхность, равна весу цилиндра жидкости, ограниченного снизу поверхностью, а сверху плоскостью гидростатического напора (рис.2,а) проходит через ц.т. объема

F_верт = ρgW.

Призма над криволинейной поверхностью называется телом давления.

Объем тела давления W не обязательно совпадает с действительным объемом сосуда. Если жидкость находится под криволинейной поверхностью, объем тела давления определяется объемом над поверхностью до плоскости гидростатического напора, а сила направлена вертикально вверх (рис.2,б).

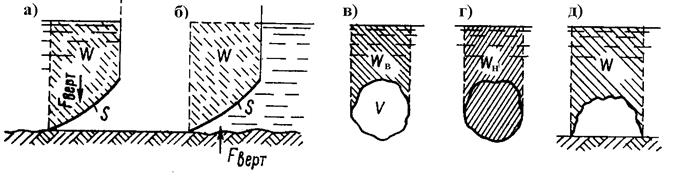
Рис.2. Силы давления на криволинейные поверхности.

Когда тело плавает на поверхности жидкости, объем тела давления равен объему вытесненной им воды V, т.е. объемному водоизмещению (рис.2 в,г)

F = ρgV.

Когда тело полностью погружено в жидкость, объем тела давления верхней половины его поверхности равен W_в, а нижней -W_н.

Вертикальную составляющую в таких случаях называют силой выталкивания (для плавающих тел - сила поддержания или плавучести)

F = ρg(W_н – W_в) = ρgV.

В результате получаем закон Архимеда: на погруженное в воду тело действует сила, равная весу вытесненной им воды, и направленная по вертикали вверх. Линия действия этой силы проходит через центр тяжести вытесненного объема V.

Закон Архимеда в обычной форме не применим к телам имеющие контактные со стенками сосуда поверхности, между которыми не может проникнуть жидкость. Такое тело испытывает со стороны жидкости только усилие ρgW, прижимающее его к грунту (рис.2,д). Но как только на контактную поверхность просочится жидкость, появится выталкивающая тело сила.

Гидродинамика

Гидродинамика изучает движение жидкости, которое может быть установившимся и не установившимся.

Движение называется установившимся, если в каждой точке неподвижного пространства, занятого движущейся жидкостью, ско-

рости не зависят от времени и, следовательно, остаются постоянными. В противном случае движение является неустановившимся.

Характер движения жидкости может быть ламинарным и турбулентным. Под ламинарным движением жидкости понимают такое движение, в котором отсутствует пульсация скоростей, приводящая к перемешиванию частиц. Если движение жидкости происходит с пульсацией скоростей, вызывающей перемешивание частиц потока, то такое движение называется турбулентным.

В гидродинамике используется понятие о линиях тока. Линии тока - линии, касающиеся вектора скорости потока. При установившемся движении жидкости линии тока и траектории движения частиц жидкости совпадают, при неустановившемся - не совпадают.

Поверхность, образуемую линиями тока, проходящими через замкнутый контур, называют трубкой тока; жидкость, заполнившая трубку тока, - элементарной струйкой.

Наглядное представление о линиях тока дает рассмотрение обтекания крыла самолета равномерным потоком воздуха. Из рис.3. видно, что снизу линии тока не очень сильно искажены, т.к. там увеличение скорости потока незначительно. Верхняя сторона крыла гораздо сильнее изменяет течение воздуха - там линии тока сжимаются и скорость заметно больше, чем в самом потоке.

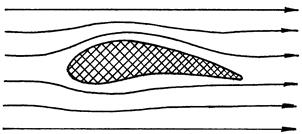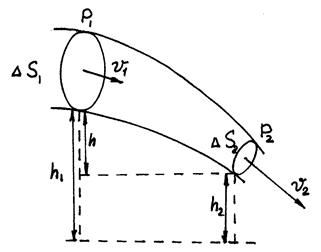Рис.3. Обтекания крыла равномерным Рис.4. К выводу уравнения

потоком воздуха. Бернулли.

Описать движение жидкости гораздо труднее, чем решить задачи гидростатики, поэтому в гидродинамике широко используют уравнения неразрывности и уравнения Бернулли.

Уравнение неразрывности выражает закон сохранения масс и используется в форме:

υ₁S₁ = υ₂S₂ = …= υ_nS_n = Q = const.

Здесь υ-скорость жидкости, S - площадь сечения трубки тока, Q - объемный расход потока. Сформулировать этот закон можно так: через любое поперечное сечение трубки тока в единицу времени протекает одинаковое количество жидкости.

Одно из важнейших уравнений гидромеханики было получено Даниилом Бернулли (рис.4.). Ему впервые удалось описать движение несжимаемой идеальной жидкости (силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда отсутствуют). Уравнение Бернулли имеет вид:

р + ρυ²/2 + ρgh = const,

где р - давление жидкости, ρ - ее плотность, υ - скорость движения, g - ускорение свободного падения и h - высота, на которой находится элемент жидкости. Уравнение Бернулли выражает закон сохранения энергии и условие неразрывности течения идеальной жидкости.

В этом уравнении все слагаемые имеют размерность давления и соответственно называются:

р - статическое давление;

ρυ²/2 - динамическое давление;

ρgh - весовое давление.

Можно отметить, что при отсутствии скорости уравнение Бернулли превращается в гидростатическую формулу. Изменение скорости, согласно второму закону Ньютона, происходит под действием силы, которая действует на жидкость, - в данном случае это либо сила тяжести, либо разность давлений, действующих на объем текущей жидкости.

В уравнении Бернулли два слагаемых:

ρυ²/2 - кинетическая энергия единицы объема движущейся жидкости и ρgh - потенциальная энергия единицы объема жидкости,

точно такие, как в уравнении сохранения энергии для материальной точки. Специфика гидромеханики проявляется в присутствии давления р - перепад давлений в разных частях трубки тока заставляет жидкость двигаться с ускорением, и именно поэтому в формуле Бернулли помимо кинетической и потенциальной энергий единицы объема жидкости присутствует еще и давление.

Следовательно, если труба (или трубка тока) устроена так, что давление в ней остается постоянным, уравнение Бернулли для жидкости просто совпадает с законом сохранения энергии для материальной точки. Если же труба устроена так, что можно не учитывать изменение высоты h (в силу малой плотности вещества или малого изменения этой высоты), то в соответствии с уравнением неразрывности скорость в узких участках трубы растет, - значит, там должно падать давление. Это естественный результат, поскольку рост скорости (ускорения) может быть обеспечен только за счет перепада давления и в том месте, где скорость большая, давление должно быть мало.

Уравнение Бернулли просто объясняет множество явлений рассматриваемых в курсе “теория судна”. Например, крыло, которое обтекает равномерный поток воды даже при отсутствии угла атаки, имеет подъемную силу. На суда идущими параллельным курсом слишком близко один к другому, действует гидродинамическая сила, толкающая их друг к другу. Большие скорости потока жидкости, создающиеся при быстром вращении судового винта, приводят к появлению кавитации, способной разрушить его лопасти. Принцип работы судового лага, основан также на уравнении Бернулли, позволяющий измерить скорость движения жидкости.

Основы теории крыла

Гребные винты, рули, и другие судовые устройства имеют общий принцип действия, рассматриваемый в теории крыла. Для изучения работы этих устройств необходимо иметь представление о силах, действующих на крыло при движении.

Геометрические характеристики крыла определяются (рис.5.):

- площадью крыла F и формой проекции крыла в плане;

- длиной (размахом) крыла l - размером крыла в направлении,

перпендикулярном набегающему потоку;

- профилем крыла - сечением крыла плоскостью, перпендикулярной его размаху;

- хордой крыла b (шириной крыла) – отрезком прямой, соединяющей крайние точки профиля; при переменной по размаху крыла хорде вводится понятие средней хорды:

b_ср = F / l;

- максимальной толщиной профиля t – расстоянием между крайними точками профиля перпендикулярно хорде.

Часто пользуются безразмерными геометрическими характеристиками крыла:

- удлинением (относительным размахом) крыла λ = l /b_ср = l² /F или (для прямоугольного крыла) λ = l / b;

- относительной толщиной 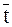= 100 t / b - отношением наибольшей толщины профиля к длине хорды.

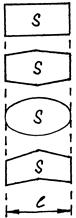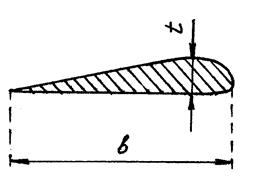Рис.5. Геометрические характеристики крыла

Гидродинамические характеристики крыла (рис.6.) определяются его геометрией и углом α между хордой профиля крыла и направлением скорости движения его, называемым углом атаки. Поток, набегающий на крыло со скоростью υ под углом атаки α, на верхней поверхности крыла ускоряется, а на нижней - замедляется. Согласно уравнению Бернулли, на нижней поверхности создается повышенное давление, а на верхней - пониженное. Кроме сил давления, на движущееся в вязкой жидкости крыло действуют касательные силы трения. Силы гидродинамического давления и касательные силы трения приводятся к главному вектору гидродинамических сил Р.

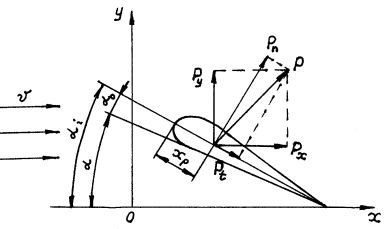
Рис.6. Схема действия потока жидкости на крыло

Спроектировав главный вектор на направление движения и перпендикулярное ему направление, получим силу профильного Р_x и подъемную силу крыла Р_у:

Р_x = Р cos(Р, x); Р_у= Р cos(Р, y).

Также можно определить составляющие силы Р направленных по нормали и по касательной к крылу. Нормальная составляющая силы Р:

Р_n = Р_y cos α + Р_х sin α;

Тангенциальная составляющая силы Р:

Р_t = Р_x cos α - Р_y sin α;

Точка приложения силы Р называется центром давления. Центр давления отстоит от передней кромки крыла на расстоянии х_р. Момент относительно передней кромки крыла М = Р_n х_р.

Отношение подъемной силы крыла к его сопротивлению называется коэффициентом гидродинамического качества крыла

К = Р_y / Р_х = С _y / С_х.

Коэффициент обратного качества ε = Р_х/ Р_y.

В соответствии с общей формулой для гидродинамических сил определяется силы и моменты, действующих на крыло при движении:

Р_y = 0,5 С _y ρ υ² F; Р_x = 0,5 С _x ρ υ² F;

Р_n = 0,5 С _n ρ υ² F; Р_t = 0,5 С _t ρ υ² F;

M = 0,5 С _m ρ υ² F b,

где С_y , С_x , С_n , С_t , С_m - безразмерные коэффициенты подъемной силы, сопротивления, нормальной силы, касательной силы и момента. Отношение абсциссы центра давления крыла к длине хорды х_р / b = С _р, называется коэффициентом центра давления крыла, тогда

С _m = С _n С _р.

Безразмерные коэффициенты определяют гидродинамические характеристики крыла. Обычно задают независимые коэффициенты: С_y, С_x , С_m (С_р), так как остальные коэффициенты являются зависимыми.

Для данного крыла коэффициенты С_y ,С_x , С_n ,С_t , С_р ,С_m , К(ε) зависят от угла атаки α, чисел Рейнольдса Re, Фруда Fr, а также от условий движения крыла (в безграничной жидкости, вблизи свободной поверхности жидкости, кавитации и т.п.). Они определяются теоретическим или чаще экспериментальным путем, поэтому для геометрически подобных крыльев они задаются в функции от угла атаки при установившемся обтекании потоком жидкости с некоторым числом Re. Значения гидродинамических коэффициентов крыла, в общем случае завися от числа Re, однако, при обтекании крыла без кавитации безграничным потоком несжимаемой жидкости с числом Re > (1,31,5) 10⁶ коэффициенты оказываются в автомодельной области и их можно считать независимыми от Re.

На рис.7. приведены кривые зависимости гидродинамических характеристик крыла от углов атаки. Из рисунка видно, что коэффициент подъемной силы с увеличением угла атаки вначале возрастает, а затем, достигнув максимума при так называемом критическом угле атаки α_кр, начинает резко падать. Для симметричного профиля подъемная сила становится равной нулю при нулевом угле атаки, для несимметричного -при значениях α, отличных от нуля. Угол атаки, при котором С_y обращается в нуль, называют углом нулевой подъемной силы α₀, а угол α_i = α + α₀ - гидродинамическим углом атаки. Направление потока, соответствующее углу α₀, называется направлением нулевой подъемной силы.

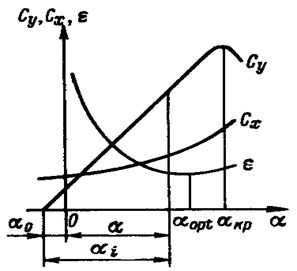
Рис.7. Кривые зависимости гидроди-намических характеристик крыла от углов атаки

Из рис.7. следует, что существует такое значение угла атаки, при котором коэффициент обратного качества минимальный. Этот угол называют наивыгоднейшим углом атаки α_орt.

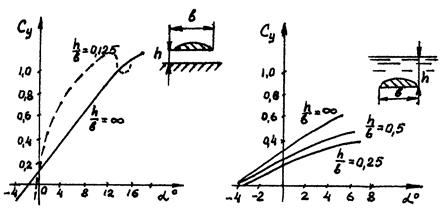На гидродинамические характеристики крыла сильно влияют границы потока (рис.8). Влияние твердой стенки под крылом приводит к увеличению коэффициента его подъемной силы, а по мере уменьшения погружения крыла к заметному снижению величины С _y.

Рис.8. Графики влияния твердой стенки и свободной поверхности жидкости на С _y прямоугольных крыльев.

Глава 3

Геометрия корпуса судна

Теоретический чертеж

Ввиду сложности формы обводы корпуса задаются графически в виде теоретического чертежа. На теоретическом чертеже изображены проекции на главные взаимно перпендикулярные плоскости линии пересечения теоретической поверхности корпуса с плоскостями, параллельными главным плоскостям. Под теоретической поверхностью понимают внутреннюю поверхность обшивки корпуса (без учета толщины обшивки и выступающих частей). Исключения составляют суда с деревянными и пластмассовыми корпусами, для которых на теоретическом чертеже изображают наружную поверхность корпуса.

В качестве главных плоскостей принимают:

- диаметральную плоскость (ДП) - вертикальную продольную плоскость, делящую корпус судна на две симметричные части - правую (правый борт) и левую (левый борт);

- плоскость мидель шпангоута ( 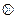) - вертикальную поперечную плоскость, проходящую по середине длины судна и делящую корпус на носовую и кормовую части;

- основную плоскость (ОП) - горизонтальную плоскость, проходящую через нижнюю точку теоретической поверхности корпуса судна в плоскости мидель-шпангоута.

Линии пересечения теоретической поверхности корпуса с плоскостями параллельным ДП называют батоксами, с плоскостями параллельными ОП - теоретическими ватерлиниями (ВЛ), с плоскостями, параллельными плоскости мидель–шпангоута - теоретическими шпангоутами.

Линии пересечения ОП с ДП и ОП с плоскостью мидель-шпангоута дают продольную и поперечную основные линии.

Пересечение ДП с корпусом образуют линию киля, форштевня, ахтерштевня и верхней палубы.

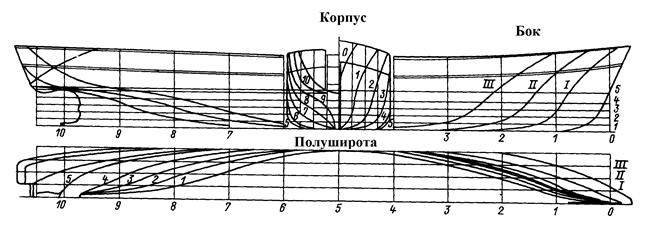
Совокупность проекций батоксов, теоретических ватерлиний и шпангоутов на ДП называется боком, на ОП - полуширотой, на плоскость мидель - шпангоута - корпусом. Эти три вида и составляют теоретический чертеж судна (рис. 9).

Рис.9. Теоретический чертеж судна

Каждое сечение проектируется на одну из плоскостей в своем истинном виде, а на две другие в виде прямых линий. Например, на виде «бок» в истинном виде представлены батоксы, а теоретические шпангоуты и ватерлинии в виде прямых. Из последних выделяют

конструктивную ватерлинию (КВЛ), по которую судно плавает с полной нагрузкой по проектную осадку. Любая другая ватерлиния, соответствующая конкретному случаю нагрузки называется действующей (расчетной) и обозначается (WL).

Число теоретических шпангоутов, как правило, принимается равными 11 или 21, которые образуют соответственно 10 или 20 теоретических шпаций.

Линии пересечения диаметральной плоскости с вертикальными поперечными плоскостями, проходящими через крайнюю носовую точку КВЛ и точку ее пересечения с осью баллера, называется соответственно носовым (НП) и кормовым (КП) перпендикулярами. При отсутствии баллера кормовой перпендикуляр получают, проводя вертикальную поперечную плоскость на расстоянии 97% длины судна по КВЛ от носового перпендикуляра.

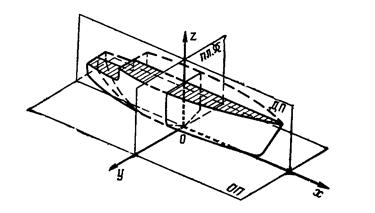
Рис.10. Главные плоскости теоретического чертежа

Для расчета статики судна используют прямоугольную систему координат oxyz (рис. 10). Координатные плоскости системы oxyz совпадают с диаметральной плоскостью (ДП) xoz, плоскостью мидель - шпангоута yoz и основной плоскостью xoy. Начало координат располагают в точке 0, а оси направляют соответственно в нос, на правый борт и вертикально вверх.

Теоретический чертеж предназначен для наглядного изображения обводов корпуса, расчетного определения характеристик эксплуатационных качеств судна, разработки проектных чертежей.

Расчеты мореходных качеств судна в условиях его эксплуатации проводятся по документации, в которой используются данные, полученные из теоретического чертежа. Теоретический чертеж применяется при проведении ремонтных работ по корпусу, при доковании судна.

Посадка судна

Посадкой называется положение судна относительно спокойной поверхности воды. Положение действующей ватерлинии относительно корпуса, а значит, и посадку судна в общем случае определяют три параметрами:

- d - средняя осадка (осадка на миделе);

- D_f - дифферент (разность осадок носом и кормой);

- Θ - угол крена - наклонение судна в плоскости мидель-шпангоута.

Наклонение судна в диаметральной плоскости можно выразить также и через угол дифферента Ψ.

Угол дифферента связан с дифферентом D_f

tg Ψ = = .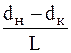

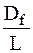При малом значении угла Ψ можно считать, что tg Ψ⁰ 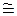Ψ Ψ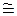⁰/57,3, тогда Ψ⁰ = 57,3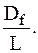

При принятой системе координат положительным считается дифферент на нос(Ψ >0), а угол крена - на правый борт (Θ >0).

Возможны следующие случаи посадки:

А. Судно плавает прямо и на ровный киль (Θ = 0, Ψ = 0). В этом случае посадка характеризуется только одним параметром - средней осадкой d.

Б. Судно плавает прямо, но с дифферентом (Θ = 0, Ψ 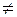0). В этом случае посадка характеризуется двумя параметрами в одном из следующих сочетаний:

- средней осадкой d и углом дифферента Ψ;

- средней осадкой d и дифферентом D_f;

- осадками носом d_н и кормой d_к, измеряемые соответственно на носовом и комовом перпендикулярах.

Названные выше параметры связаны между собой следующими зависимостями:

Ψ⁰ = 57,3 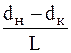; d = .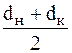

В. Судно плавает на ровный киль, но с креном (Ψ = 0, Θ 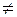0). В этом случае посадка характеризуется двумя параметрами - средней осадкой d и углом крена Θ.

Г. Общий случай посадки (судно плавает с креном и дифферентом). Посадка характеризуется тремя параметрами в одном из следующих сочетаний:

d, Ψ и Θ; d_н, d_к и Θ; d, D_f и Θ.

Для контроля за осадкой судна при изменении его нагрузки, а также для определения его дифферента используют марки углубления.

Марки углубления наносят на обоих бортах судна в носу и

корме, а также в районе мидель-шпангоута. Высота цифр, измеренная по нормали к ОП, равна 1 дм (100 мм), расстояние между ними также 1 дм (100 мм), или соответственно 50 мм и 50 мм; при нанесении марок углублений в футах высота цифр и интервал между ними принимаются равными 0,5 футам (6 дюймам). Метрические марки наносятся арабскими цифрами, футовые - римскими (рис.13). По маркам углубления замеряют габаритную осадку т.к. нижняя кромка каждой цифры показывает расстояние по вертикали до нижней кромки горизонтального киля. Кроме того, марки углубления не обязательно располагаются на носовом и кормовом перпендикулярах судна.

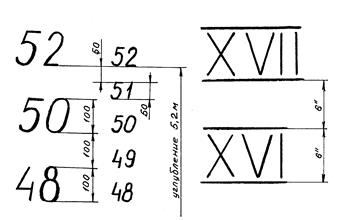
Рис.13. Марки углублений

Судовая документация, служащая для оценки мореходных качеств судна рассчитывается и строится для осадок, отсчитываемых на перпендикулярах от основной плоскости судна. Поэтому для их получения необходимо значения осадок снятые с марок углублений исправить с помощью специальной шкалы (рис.14).

При отсутствии указанной шкалы осадки на перпендикулярах определяются по формулам:

d_н = d_нм 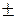d_нм + (L /2 – l) Ψ; d_к = d_км 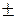d_км – (L /2 – l) Ψ,

где d_нм и d_км - отстояние от основной плоскости нижней кромки киля в плоскостях носовых и кормовых марок углубления (знак плюс, когда кромка проходит ниже основной плоскости, минус - выше ос-

новной плоскости), l₁ и l₂ - отстояние носовых и кормовых марок углубления от плоскости мидель-шпангоута.

На некоторых судах для определения осадок устанавливаются осадкомеры, показания от которых автоматически передаются на мостик.

Угол крена на судах замеряется кренометром. Для замера угла дифферента некоторые суда могут иметь специальные приборы - дифферентометры.

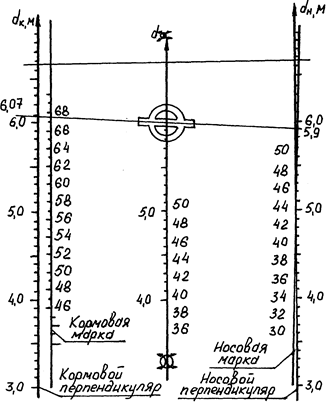
Рис.14. Шкала, связывающая осадки на

перпендикулярах с осадками на

марках углубления т/х «А. Сафонцев»

Глава 4

Плавучесть судна

Условие плавучести судна

Плавучестью называется способность судна плавать в состоянии равновесия в заданном положении относительно поверхности воды при заданной нагрузке.

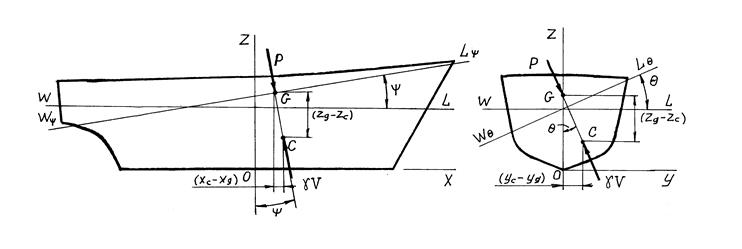
На судно, плавающее без хода на спокойной воде, действуют две категории сил: силы тяжести и силы избыточных гидростатических давлений (рис.26). Силы тяжести представляют собой силы тяжести корпуса, механизмов, систем и устройств, запасов, экипажа и др. Силы тяжести приводятся к одной равнодействующей - силе тяжести судна Р, которая направлена вертикально вниз и приложена в центре тяжести судна(ЦТ) - в точке G с координатами x_g , y_g , z_g .

Рис. 26. К составлению уравнений равновесия плавающего судна

Силы избыточных гидростатических давлений, действующие на поверхность погруженной части корпуса судна, также приводятся к одной равнодействующей – гидростатической силе поддержания (силе плавучести).

Сила плавучести направлена вертикально вверх и приложена в центре величины судна (ЦВ) - в точке С с координатами x_с, y_с, z_с. Центр величины представляет собой геометрический центр подводного объема судна V и его положение зависит от формы корпуса судна и его посадки.

Условия равновесия плавающего судна:

1.Сила тяжести (масса) судна равна весу (массе) вытесненной им воды:

Р = γV; Δ = ρV.

где V- объемное водоизмещение судна м³,

γ - удельный вес воды (.γ = 10,05 кН/м³- для морской и γ = 9,81 кН/м³ - для пресной воды),

ρ - плотность воды (ρ = 1,025 т/м³- для морской и ρ = 1,0 т/м³- для пресной воды).

2.Центр тяжести (ЦТ) и центр величины (ЦВ) судна лежат на одной вертикали, перпендикулярной к плоскости ватерлинии (рис.26);

(x_с - x_g) + (z_c – z_g) tg Y = 0;

(y_с - y_g) + (z_c – z_g) tg Q = 0,

где x_с, y_с и z_c – координаты центра величины судна;

x_g ,y_g и z_g – координаты центра тяжести судна.

Если судно сидит прямо и на ровный киль (Y = Q = 0), то уравнение принимает вид:

x_g = x_с; y_g = y_с.

В практических расчетах судна, плавающего с дифферентом, часто пренебрегают величиной (z_c – z_g) tg Y по сравнению x_с, т.е. полагают, что x_с ≈ x_g. Принятое допущение дает незначительную ошибку при определении элементов плавучести судна.

Или расходование грузов

В теории судна принято разделять грузы на “малые грузы” и “большие грузы”. Под “малыми грузами” понимают грузы масса которых не превосходит 10 ÷ 12 % водоизмещения судна. Грузы большей массы относятся к категории “больших грузов”. Такое разделение определяется методикой определения изменения мореходных качеств судна. Изменение параметров посадки, остойчивости при приеме или расходовании малого груза можно определить путем проведением расчетов с использованием довольно простых формул. При рассмотрении большого груза применение формул не приемлемо, т.к.

это дает значительную погрешность. В таких случаях используют судовую документацию.

4.4.1. Изменение посадки при приеме или расходовании “малого груза”.При приеме малого груза (массой m), происходит увеличение водоизмещения судна на величину ρdv. Считаем, что судно прямобортное и поэтому в процессе приема меняется средняя осадка dd, а площадь действующей ватерлинии S не изменяется.

Δ = ρdv, т.к. dv = dd·S,

Получим формулу изменения средней осадки:

dd = m / ρS (м),

где: S – площадь ватерлинии находят по кривой S(d) входящей в КЭТЧ (кривые элементов теоретического чертежа). При расходовании груза перед m ставится знак минус.

В грузовой шкале (рис.23.), а также в кривых элементов теоретического чертежа приведены значения q_см (d) = 0,01 ρS (число тонн на 1 см осадки) и моментов дифферентующий на 1 см (m_Д), при помощи которых можно быстро определить изменение средней осадки и дифферента:

dd = m /q_см (см).

Использование данной формулы при приеме (расходовании) большого груза, за исключением судов с α = 1, не обеспечивает необходимую точность расчета, т.к. q_см и S меняется в зависимости от осадки судна.

Изменение осадок при приеме “малого груза” массой m с абсциссой х определяют по моменту дифферентующему на 1 см, m_Д:

dD_f = m (х –x_f)/100 m_Д;

δd_н = δd +(0,5L – x_f ) dDf/ L; δd_к = δd – (0,5L + x_f ) dDf/ L.

4.4.2. Изменение посадки при приеме или расходовании “больших грузов”.При приеме (расходовании) больших грузов изменение средней осадки можно найти по грузовому размеру (рис.22.) или грузовой шкале, как разность осадок, соответствующих прежнему и новому водоизмещению.

При наличии у судна дифферента, эта задача может быть решена при помощи дифферентных диаграмм а также специальной шкалы для определения изменения осадок носом и кормой от приема 100 т. груза (рис.27).

Рассмотрим порядок расчетов с помощью диаграммы Г.А.Фирсова (рис.25,а).

При приеме груза массой m в точку с абсциссой х момент массы судна относительно плоскости мидель - шпангоута становится Δ ₁х_g1.

Δ ₁х_g1 = Δ х_g + mх,

где Δ и х_g масса и абсцисса центра тяжести судна до приема груза.

Абсцисса ц.т. судна с принятым грузом: х_g1 = Δ ₁х_g1/(Δ + m).

Полагая х_g ≈ х_с и х_g1≈ х_с1 , по известным х_g1 и Δ ₁ находим по диаграмме новые значения осадок d_н1 и d_к1.

Подобным путем можно решить обратную задачу по определению массы и координаты центра тяжести снимаемого груза для обеспечения заданной посадки судна.

Оперативный контроль за изменением осадок можно выполнить по шкале изменения осадок оконечностей от приема 100 т груза, показанным на рис.27. По известной абсциссе центра массы принимаемого (снимаемого) груза и средней осадке или массы определяют δd_н0, δd_к0 и рассчитывают изменение осадок от приема груза массой m по формулам:

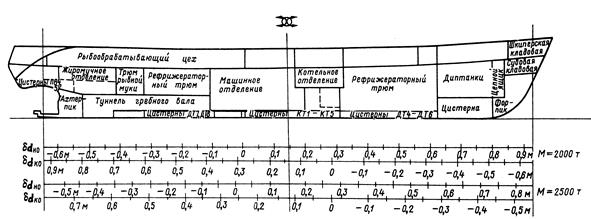δd_н = m δd_н0/100; δd_к = m δd_к0/100.

Рис.27. Шкала для определения осадок носом и кормой от приема 100 т груза

4.4.3. Изменение посадки при перемещении грузов.Пусть осадки судна массой Δ с абсциссой х_с до перемещения груза были d_н и d_к. На диаграмме Г.А. Фирсова операция перемещения груза массой m на расстояние l_x лежит на кривой Δ = const.

х_с1 = (m l_x + Δ х_с)/ Δ.

По известному х_g1≈ х_с1 находим новые значения осадок d_н1 и d_к1.

В случае определения массы перемещаемого груза при заданных осадках d_н1 и d_к1 используют уравнение:

m l_x = Δ (х_с1 - х_с).

Рис.28. Чертеж размещения грузов на судне

§ 4.5. Запас плавучести судна

Из первого условия равновесия следует, что плавучесть судна обеспечивается возможностью уравновесить силу тяжести Р силой плавучести γV. Поэтому величина силы плавучести может быть принята в качестве меры плавучести судна. Поскольку удельный вес воды γ, изменяется в очень узких пределах, практически мерой плавучести судна может являться объемное водоизмещение V, т.е погруженный объем корпуса, можно рассматривать как израсходованную плавучесть на компенсацию силы тяжести судна. Плавающее судно располагает и неизрасходованной плавучестью, определяемой непроницаемым для воды объемом корпуса, находящегося выше ватерлинии. Этот объем носит название запаса плавучести.

Запас плавучести, выраженный в процентах от объемного водоизмещения судна, на промысловых судах составляет 25 ÷ 30%, на танкерах 10 ÷ 15%, на пассажирских судах 80 ÷ 100%.

Необходимый запас плавучести судна обеспечивается назначением ему минимальной высоты надводного борта, достаточной для бе