Различение двух сигналов с неизвестными начальными фазами и интенсивностями.

Колебания u(t), поступающие на вход радиоприемной системы на интервале наблюдения tÎ(0,T), представляют собой аддитивную смесь

u(t)=s_i(t,j,e)+ n(t) , i=1,2 (4.9.1)

помехи n(t) и одного из двух сигналов s₁(t,j,e) или s₂(t,j,e), являющихся известными функциями времени t и двух случайных несущественных параметров: начальной фазы j и параметра интенсивности e , так что

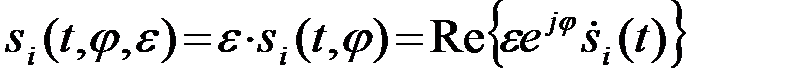, i=1,2 . (4.9.2)

Априорные вероятности посылки сигналов s₁ и s₂ полагаются одинаковыми P₁=P₂=0.5. Считаются также заданными статистика помехи n(t) и закон распределения P(j,e) несущественных параметров j и e. Требуется определить оптимальный алгоритм обработки наблюдения{u(t),tÎ(0,T)}при принятии решений 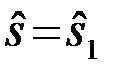или .

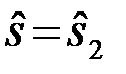Настоящая задача отражает реальные условия работы РТС при наличии замираний, т.е. флюктуаций интенсивности (амплитуды) принимаемых сигналов. Флюктуации амплитуды сопровождаются флюктуациями фазы и обычно являются результатом интерференционного характера поля принимаемого сигнала.

В соответствии с общим решением задачи различения, оптимальная система по наблюдению должна сформировать и сравнить между собой две условные ПВ этого наблюдения p( |s₁) и p( |s₂) при условии, что послан сигнал s₁ или s₂. Аналитически заданными в рассматриваемой задаче являются ПВ p( |s₁,j,e) и p( |s₂,j,e). Условная ПВ вектора наблюдений при условии, что передается сигнал s₁ с данными значениями jи eнесущественных параметров выражается формулой

. (4.9.3)

Если воспользоваться обозначениями, введенными при выводе (4.6.11), то

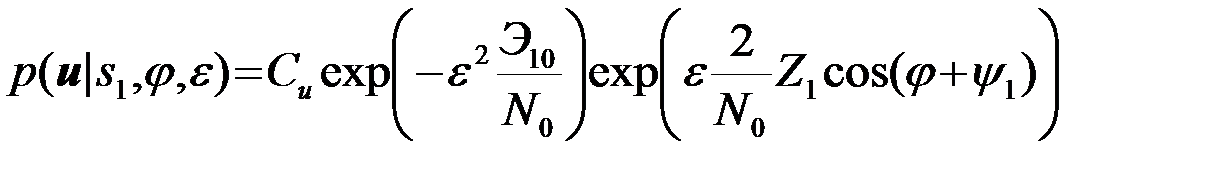. (4.9.4)

В (4) Э₁₀и далее Э₂₀ обозначают интегралы 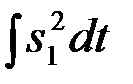и 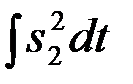по интервалу 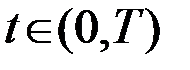. Энергия принимаемых сигналов равна 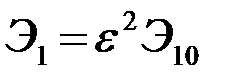и 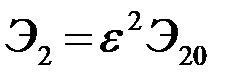. Выражение для p( |s₂,j,e) получается заменой индекса 1 в (4) на 2. Интересующие нас ПВ p( |s₁) и p( |s₂) определяются усреднениемp( |s₁,j,e)и p( |s₂,j,e) по несущественным параметрам jи e

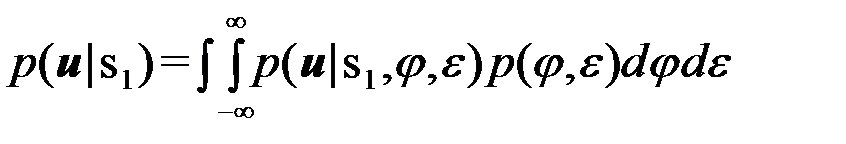. (4.9.5)

Для дальнейшего решения задачи нужно конкретизировать вид распределения p(j,e). Имеется большое разнообразие практических ситуаций, связанных с флуктуациями фазы и амплитуды принимаемых сигналов. Мы ограничимся рассмотрением наиболее характерного случая, что позволяет сосредоточить внимание на общих закономерностях и современных методах анализа и синтеза РТС. Несущественные параметры полагаются независимыми случайными величинами, причем j распределено равновероятно в интервале jÎ(0,2p), а распределение интенсивности p(e)не конкретизируется (в большинстве случаев распределение аппроксимируют законом Релея)

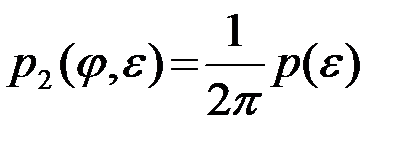, jÎ(0,2p), eÎ(0, ¥). (4.9.6)

Усреднение (5) по jдля распределения (6) аналогично усреднению (4.6.11) (i=1 или 2)

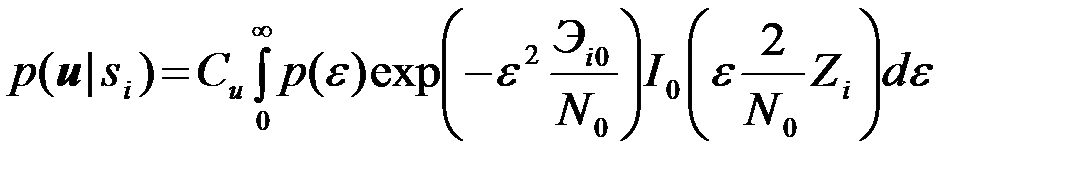(4.9.7)

При различении нулевого и ненулевого сигналов s₁=s, Э₁₀=Э₀ , Z₁=Z, a s₂=0, Э₂₀=0, Z₂=0 и

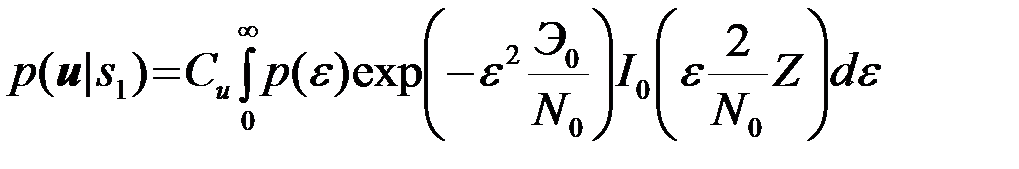, (4.9.8)

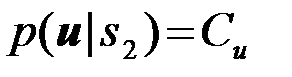. (4.9.9)

При данных, заданных условиями задачи, значениях Э₀ и N₀ интеграл, входящий в (8) зависит только от Z. Обозначим его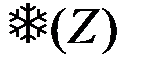

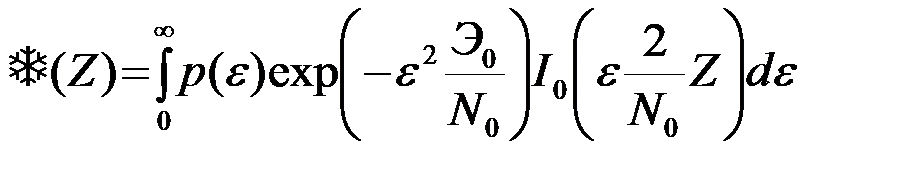. (4.9.10)

Функция 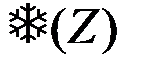является монотонно возрастающей функцией Z, так как все множители под знаком интеграла неотрицательные функции, причем одна из функций тем больше, чем больше Z. Примерный вид функции 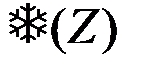изображен на рис. 4.21. Точный вид функции зависит от закона распределения p(e).

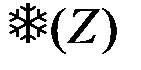
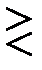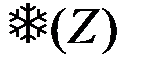
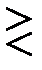
Оптимальное правило принятия решений в настоящем случае выражается неравенством C_u C_u или , которое может быть преобразовано к виду:

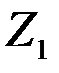
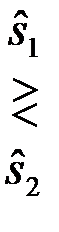
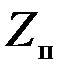(4.9.11)

где пороговое значение Z_п величины Z определяется из уравнения 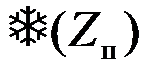=1 (рис.4.21).

При различении сигналов с одинаковыми энергиями Э₀₁=Э₀₂=Э₀,

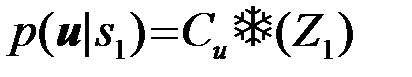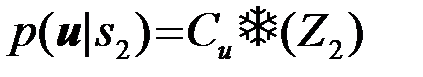, (4.9.12)

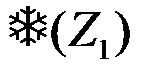
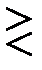
и оптимальное правило принятия решений 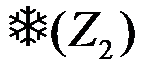, можно представить в виде

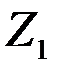
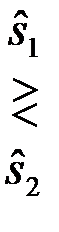
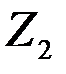. (4.9.13)

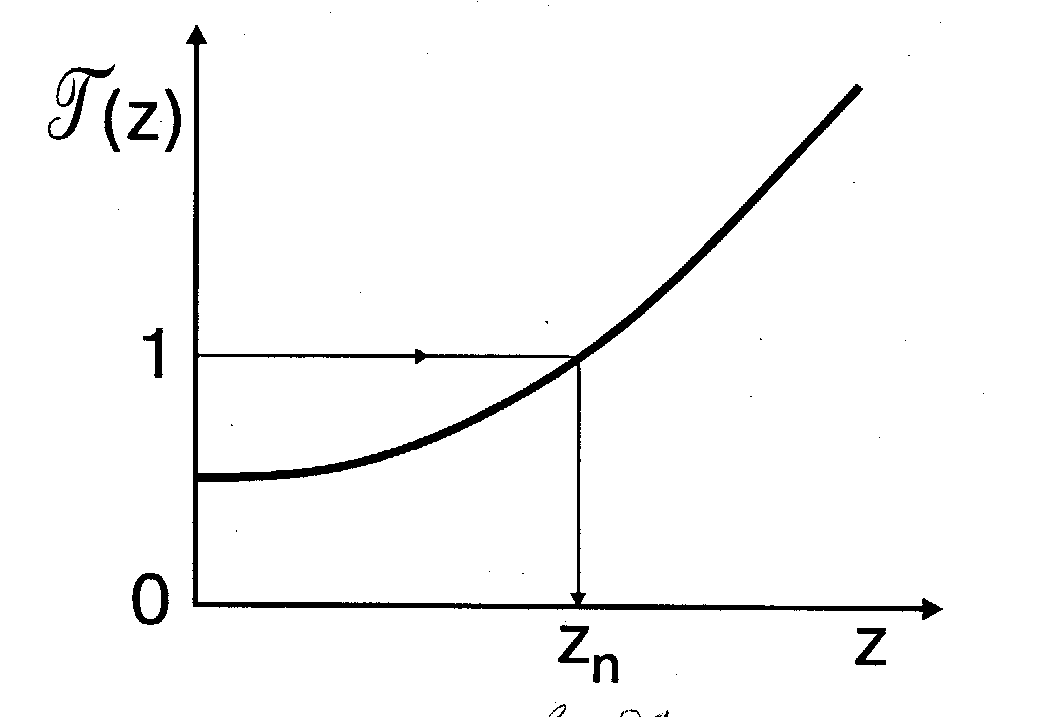
Рис. 4.21

Таким образом, оптимальная система обработки при приеме сигналов с неизвестными начальной фазой и интенсивностью получается такой же, как и при приеме сигналов с неизвестной начальной фазой и фиксированной интенсивностью. Опять основной существенной операцией является операция формирования модульного значения комплексного корреляционного интеграла принимаемого колебания с образцами всех различаемых сигналов. Причем, начальная фаза и интенсивность (масштабный множитель) образцов сигналов, входящих в корреляционный интеграл, могут выбираться произвольно. Можно сказать, что радиоприемное устройство наилучшим образом спроектированное для приема сигналов известной интенсивности, будет также наилучшим при приеме сигналов неизвестной интенсивности. Точное значение порогового уровня Z_п в системе различения нулевого и ненулевого сигналов зависит от закона распределения p(e) параметра интенсивности e. Вероятность ошибок различения для конкретной реализации наблюдения определяется энергией фактически принятого сигнала e²Э₀. Для расчета вероятности ошибок средней по ансамблю реализаций сигнала со случайной интенсивностью также должно быть задано распределение p(e). Пример такого расчета будет приведен в главе 5.

Закономерности, полученные в задаче различения двух сигналов, в значительной мере носят общий характер и сохраняются при различении произвольного числа M сигналов.

Различение M сигналов

В параграфе обсуждаются цифровые сигналы связного типа альтернативные по отношению к сигналам КИМ и их оптимальный прием.

4.10.1. Недостаток сигналов КИМ. В настоящее время, когда требуется большая дальность и высокая надежность связи, широко используются цифровые методы связи. При этом объектами передачи являются целые числа N_i , принадлежащие множеству {0,1,..., M-1} или {1,2,..., M} и следующие друг за другом с интервалом дискретности, определяемым теоремой отсчётов. В большинстве случаев передаваемые числа записываются в двоичной системе счисления и передаются посредством сигналов КИМ. Однако сигналы КИМ не являются наилучшим видом сигналов. Можно предложить сигналы, которые при той же энергии обеспечивают большую надежность связи (меньшую вероятность ошибочных решений Р_ош.ср.) или при той же надежности связи требуют меньшей затраты энергии.

Поясним основной недостаток сигналов КИМ. Для этого положим, что элементарные сообщения N_i могут принимать значения 0,1, ...,127 и при использовании сигналов КИМ представляют собой семиразрядные ( 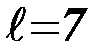) двоичные числа. Рассмотрим два сообщения N₁и N₂:

N₁ =1010101=85;

N₂ =1110101=117.

На рис. 4.22 приведены два сигнала КИМ ФМ s₁(t) и s₂(t), соответствующие сообщениям N₁ и N₂. Сигналы занимают семь подинтервалов длительностью D и состоят из семи следующих друг за другом радиоимпульсов, начальная фаза которых равна 0 или p, в зависимости от того, передается 1 или 0. Обозначим энергию элементарных импульсов Э₀. Тогда полная энергия сигналов s₁(t) и s₂(t) будет равна 7Э₀. Недостаток состоит в том, что сигналы s₁ и s₂точно совпадают друг с другом на 6 подинтервалах и отличаются только на одном, а именно, на втором подинтервале.

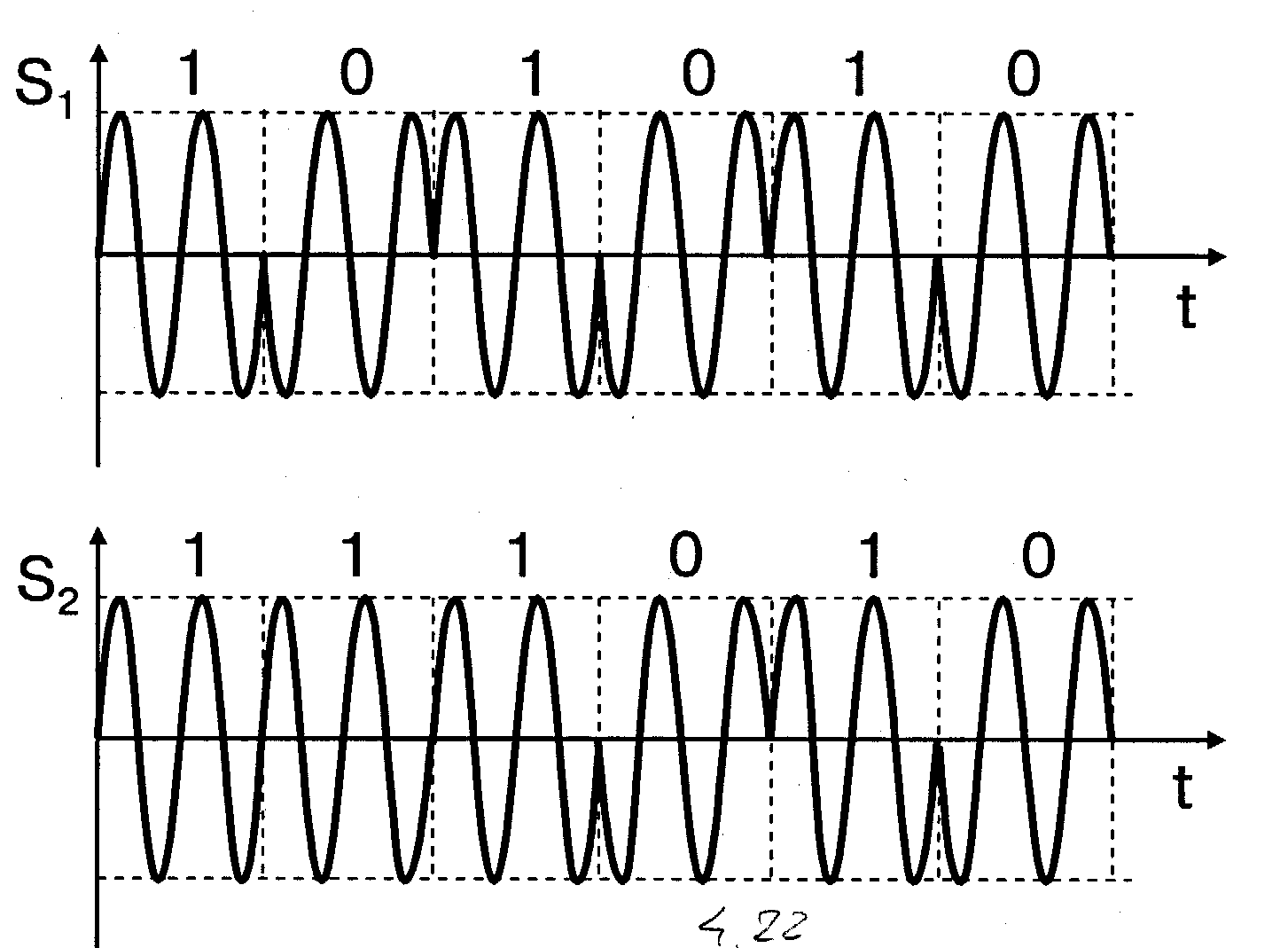
Рис. 4.22

В соответствии с закономерностью, сформулированной п.4.5.4, для различения этих сигналов (s₁ и s₂) используется только энергия несовпадающей части (энергия разностного сигнала s_q=s₁-s₂), тогда как остальная часть, составляющая 6/7 полной энергии каждого из сигналов, не используется - теряется бесполезно. Этот же результат можно выразить в терминах коэффициента корреляции сигналов s₁ и s₂:

.

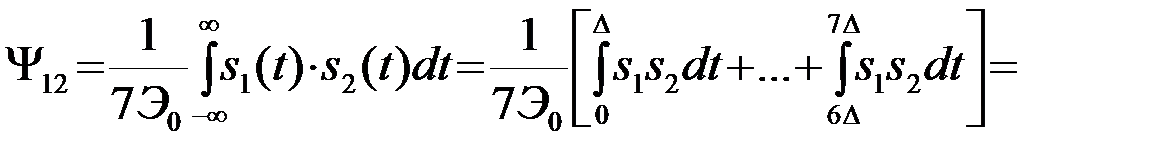
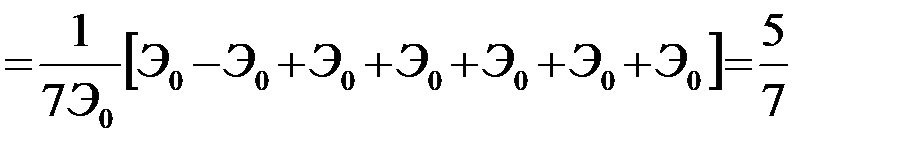Таким образом, в системах КИМ имеются сигналы, которые мало отличаются друг от друга или коэффициент корреляции которых велик. Различение таких сигналов, как было установлено выше, связано с энергетическими потерями. Если бы сигналы были не коррелированны (или при когерентном приеме - отрицательно коррелированны), для обеспечения заданной надежности связи потребовалась бы значительно меньшая энергия сигналов.

На основании проведенного обсуждения можно сделать следующее заключение. Желательно иметь такой набор сигналов s₁(t), . . . , s_М(t) (соответствующий набору сообщений 1,2,...,M), которые бы как можно сильнее отличались друг от друга или, что то же самое, для которых максимальный коэффициент корреляции между парой сигналов s_i и s_j (i,j=1, 2,..., M; i¹j) имел бы минимально возможную величину. Теоретически доказано, что оптимальный ансамбль равновероятных сигналов должен состоять из сигналов с одинаковой энергией и удовлетворять условию

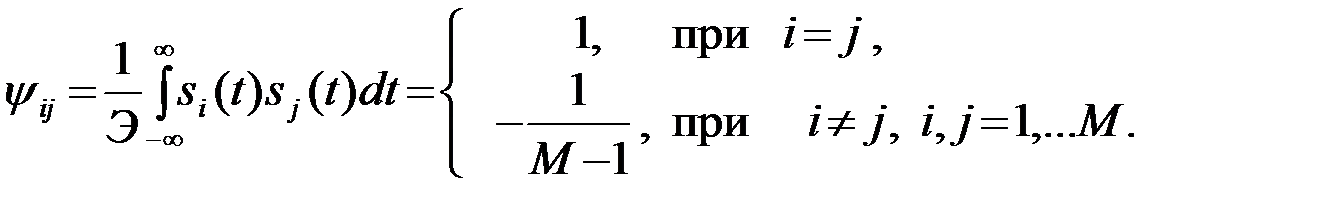(4.10.1)

Следовательно, любая пара сигналов s_i и s_j (i¹j) из оптимального ансамбля {s_i,i=1,2,...,M} имеет один и тот же коэффициент корреляции 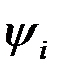который меньше нуля (отрицательный) и равен -1/(M-1). При достаточно большом M (несколько десятков и более) из (1) следует, что практически оптимальным является набор взаимно ортогональных сигналов ( 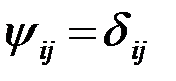), имеющих одинаковую энергию.

4.10.2. Фазоманипулированные шумоподобные сигналы. В настоящее время предложено много видов оптимальных сигналов или сигналов, приближающихся к оптимальным. Наибольшее распространение получили так называемые фазоманипулированные шумоподобные сигналы(ФМШС). Рассмотрим кратко этот вид сигналов. Обозначим сигналы, соответствующие полному набору передаваемых сообщений 1,2, . . . , M, символами s₁(t), . . . , s_М(t). ФМШС построены на базе линейных рекуррентных последовательностей двоичных чисел A_iÎ(0,1), называемых М-последовательностью. Каждому сигналу соответствует (®) код - последовательность из М двоичных чисел:

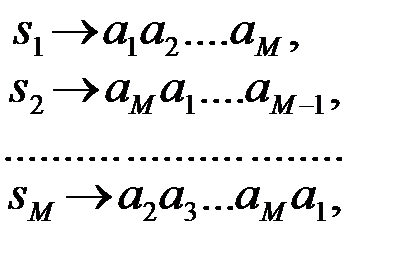(4.10.2)

Число элементарных сообщений M принимается равным целой степени 2без единицы

M = 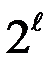- 1. (4.10.3)

Целое число ℓназывается памятью кода. Так, например, если ℓ=4, M=15, если ℓ=7, M=127, если ℓ=10, M=1023 и т.д. Как следует из кодовой таблицы (2), сигнал s_i получается из предыдущего сигнала s_i-1 путем циклической перестановки символов кода: символ с первой позиции переходит на вторую, со второй на третью и т.д. Символ с последней позиции переходит на первую. Поэтому нужно определить одну единственную кодовую последовательность, например последовательность, соответствующую сигналу s₁. Для определения одной кодовой последовательности задают произвольную(но не нулевую a₁=a₂...=a_ℓ=0) комбинацию из ℓ первых двоичных чисел a₁a₂...a_ℓ , где ℓ - память кода, связанная с длиной кодовой последовательности M соотношением (3). Все последующие элементы кодовой последовательности a_ℓ+1...a_M определяются из рекуррентной формулы

a_i=m₁a_i-1+m₂a_i-2+ . . . +m_ℓa_i-ℓ ; i > j . (4.10.4)

Коэффициенты m₁,...,m_ℓ- двоичные числа (0 или 1), определяемые по специально составленным кодовым таблицам. Суммирование в (4) ведется по модулю 2. Последовательность a₁a₂ и т. д., формируемая с помощью формулы (4) описанным способом получается периодической с длиной периода, равной M=(2^ℓ-1).

В качестве примера положим ℓ=4, M=15. Кодовая таблица при этом дает следующие значения коэффициентов в рекуррентной формуле (4)

m₁=m₄=1; m₂=m₃=0. (4.10.5)

Соответственно рекуррентная формула (4) принимает вид:

a_i=a_i-1+a_i-4, i > 4. (4.10.6)

Для построения кодовой последовательности зададим произвольную ненулевую начальную комбинацию из ℓ(в нашем примере из четырех) двоичных символов. Пусть это будет 1 1 1 1, т.е. a₁=a₂=a₃=a₄=1. Тогда на основании (6) имеем

a₅ =a₄ +a₁ =1+1=0;

a₆ =a₅ +a₂ =0+1=1 и т.д.

Получается последовательность:

[1 1 1 1 0 1 0 1 1 0 0 1 0 0 0] 1 1 1 1 0 1 0 1 1 ... (4.10.7)

После 15 символов последовательность повторяется, т.е. является периодической последовательностью с длительностью периода, равной M=(2^ℓ -1) символов.

Структура последовательности (7) подобна структуре случайной последовательности, у которой двоичные элементы (нули и единицы) определяются посредством случайного эксперимента с двумя равновероятными исходами, например, посредством метания монеты. Число нулей и число единиц примерно одинаковое. Примерно одинаковое также число пар 00, 01, 10, 11 и т.д. Поэтому последовательность вида (7) называют шумоподобной (или псевдослучайной), хотя формируется она регулярным способом.

Один период последовательности (7), заключенный в квадратные скобки, может рассматриваться как кодовая комбинация, соответствующая сигналу s₁:

s₁® 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0. (4.10.8)

Кодовые последовательности, соответствующие сигналам s₂,s₃ и т.д., получаются из (8) путем циклической перестановки элементов

s₂® 0 1 1 1 1 0 1 0 1 1 0 0 1 0 0 и т.д. s₃,...,s_M. (4.10.9)

Перейдем теперь от кодовых последовательностей, определяющих сигналы, к самим сигналам. Интервал T_c, отводимый на передачу элементарного сообщения NÎ(1,...,M), разделим на M подинтервалов длительностью D=T_c / M. Каждый подинтервал отводится для передачи одного двоичного числа кодовой последовательности при помощи ФМ радиоимпульсов. При этом нулю соответствует колебание с начальной фазой j₀, а единице - колебание с начальной фазой j₀+p (или наоборот). Амплитуда и несущая частота сигнала не меняются. Правило формирования сигналов из кодовой последовательности двоичных символов такое же, как и в системах КИМ ФМ.

Сигналы s₁(t) и s₂(t) показаны на рис.4.23. Внешне они похожи на сигналы КИМ ФМ, но имеют существенно иные свойства, в частности очень малый коэффициент корреляции .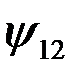

Рассчитаем теперь коэффициент корреляции 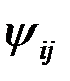между двумя сигналами, например, 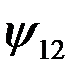между сигналами s₁ и s₂ , изображенными на рис. 4.23

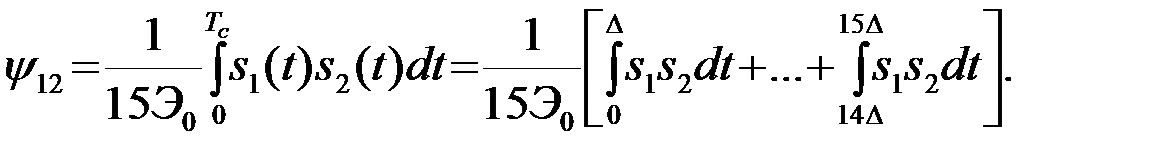(4.10.10)

Здесь Э₀- энергия сигнала на одном подинтервале, 15Э₀ - полная энергия сигнала. Интегрирование (10) будем вести по подинтервалам. Интеграл произведения s₁(t)s₂(t) по i- му подинтервалу tÎ((i-1)D,iD) равен Э₀, если начальные фазы сигналов s₁(t) и s₂(t) совпадают на этом подинтервале, и равен - Э₀ , если фазы отличаются на p. Поэтому необходимо только подсчитать число "совпадающих" и "несовпадающих" подинтервалов. Это можно сделать суммированием по модулю 2 кодовых последовательностей, соответствующих сигналам s₁ и s₂:

s₁ ® 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0

+s₂ ® 0 1 1 1 1 0 1 0 1 1 0 0 1 0 0 (4.10.11)

1 0 0 0 1 1 1 1 0 1 0 1 1 0 0 .

Число единиц в полученной сумме определяет число подинтервалов, на которых символы кода или начальные фазы сигналов не совпадают. Число нулей определяет число подинтервалов с совпадающими символами (совпадающими начальными фазами сигналов). В результате получаем

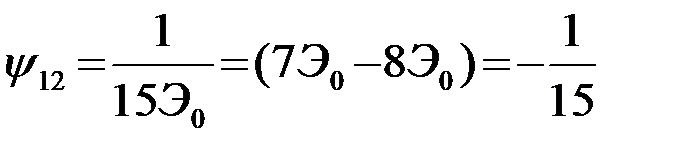. (4.10.12)

Нетрудно убедиться, что коэффициент корреляции между любыми двумя сигналами s_i(t) и s_j(t)(i¹j), полученного ансамбля сигналов, является отрицательным числом, равным -1/15. В общем случае при произвольном M=2^ℓ-1

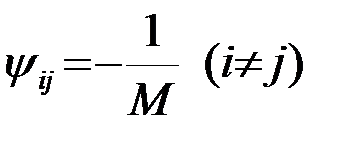. (4.10.13)

Таким образом, рассмотренный ансамбль сигналов является практически оптимальным. При M>>1 (1/M<<1) ансамбль ФМШС можно считать ансамблем взаимно ортогональных сигналов.

Введем в рассмотрение сигнал s_j^(t), квадратурный по отношению к s_j(t), и рассчитаем модульное значение комплексного коэффициента корреляции ½ 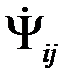½ между сигналами s_i и s_j (i¹j) Согласно определению,

.

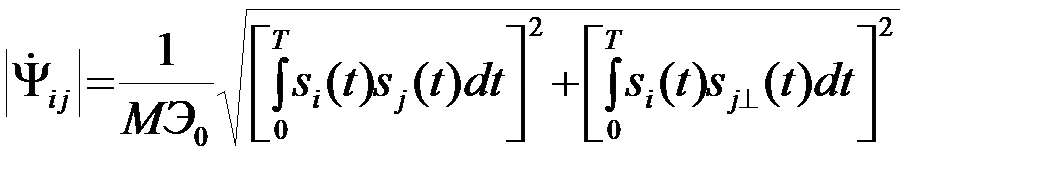Второй интеграл под радикалом в последнем выражении равен нулю, так как на любом подинтервале сигналы s_i(t) и s_j^(t), являются квадратурными (сдвинутыми по фазе на ± p/2). Поэтому

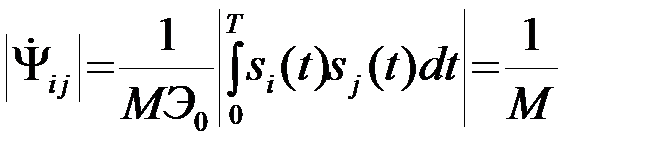. (4.10.14)

и отличается от (13) только знаком. При M>>1

½ 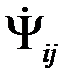½»d _{i j} ; i, j = 1 , . . . , M . (4.10.15)

Следовательно, ФМШС практически взаимно ортогональны в усиленном смысле и при их использовании возможен прием сигналов с неизвестной начальной фазой - некогерентный прием. ФМШС являются примером ансамбля сигналов, занимающих одну и ту же полосу частот и один и тот же временной интервал, и в то же время являющихся практически взаимно ортогональными в усиленном смысле.

Благоприятные корреляционные свойства ансамбля ФМШС обеспечивают существенный энергетический выигрыш (или выигрыш в помехоустойчивости) по сравнению с сигналами КИМ. Полоса частот 2F_c , занимаемая ФМШС (так же, как и полоса частот сигналов КИМ с ФМ), определяется длительностью элементарных импульсов и примерно равна 2F_с »1/ D .

Обычно задан интервал времени T_с, отводимый на передачу элементарного сообщения NÎ(1,...,M). Если задан интервал дискретности T₀ и число каналов K, то T_с =T₀ / K. При использовании сигналов КИМ на промежутке длительностью T_c размещается ℓимпульсов, несущих двоичную информацию (0 или 1), тогда как при ФМШС число двоичных импульсов на интервале T_с должно равняться числу сообщений 2^ℓ-1. Поэтому в системах с ФМШС длительность импульсов уменьшается, а полоса частот, занятая сигналом, увеличивается в (2^ℓ-1)/ℓ раз по сравнению с системами КИМ. Это значит, что повышение помехоустойчивости ФМШС по сравнению с КИМ достигается за счет увеличения ширины полосы частот, занятой сигналами. Так, например, если M=128 (127), что характерно для цифровых систем передачи речи, полоса частот, занятая сигналом при переходе от КИМ ФМ к ФМШС, увеличивается в 18 раз. При этом примерно в 2,5-3 раза уменьшается энергия порогового сигнала Э_Cmin и соответственно возрастают дальность связи и ее надежность.

На рис. 4.24 приведена практическая схема генератора шумоподобной последовательности двоичных чисел с длительностью периода M=15 (ℓ=4). Схема работает в соответствии с рекуррентной формулой (6) и генерирует последовательность двоичных чисел (7).

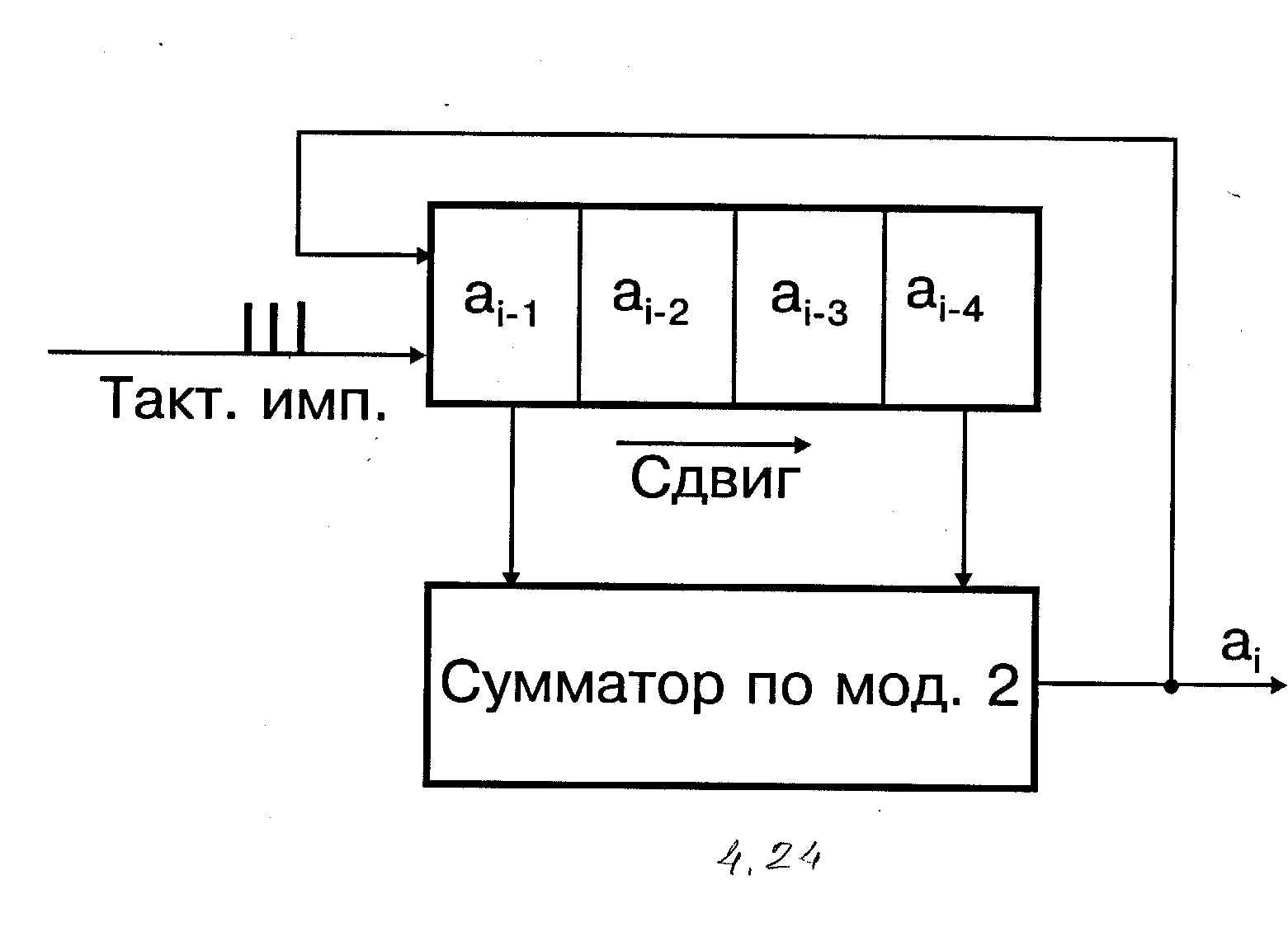
Рис. 4.24

Устройство состоит из следующих элементов: сдвигающего регистра, имеющего ℓразрядов (каждый разряд может находиться в одном из двух состояний: 0 или 1); сумматора по модулю 2; связей регистра сдвига с сумматором, соответствующих значениям m_i=1, и цепи обратной связи. Устройство работает от внешних запускающих (тактовых) импульсов, следующих друг за другом с интервалом D. На каждом, скажем i- м такте, в разрядах регистра хранятся двоичные числа: в первом разряде a_i-1, во втором разряде a_i-2 и т. д. При этом на выходе сумматора формируется число a_i . После прихода очередного тактового импульса происходит сдвиг содержимого регистра на один разряд в направлении, указанном на рис.4.24: a_i-1 записывается во второй разряд, a_i-2- в третий и т. д., а число a_i с выхода сумматора записывается в первый разряд. После прихода следующего тактового импульса описанный цикл работы повторяется. Выходная последовательность двоичных чисел может быть снята с выхода сумматора либо с любого разряда регистра сдвига.

Применение ФМШС, а также другие практические приложения порождают задачу различения M сигналов.

4.10.3. Оптимальные алгоритмы различения M сигналов. Задача формулируется следующим образом. Колебание u(t), поступающее на вход радиоприемного устройства на интервале наблюдения (0,T), представляет собой аддитивную смесь сигнала и помехи:

u(t)=s_i(t, a)+n(t); iÎ(1, . . . , M). (4.10.16)

Сигнал является одной из M известных функций (s₁, или s₂, . . . или s_M ) времени tи в общем случае случайного несущественного параметра a(скалярного или векторного).

В частном случае функции s_i с различными индексами i могут отличаться друг от друга значением информационного параметра l, т.е. представлять собой одну и ту же функцию s( ) времени t, информационного параметра l, который может принимать M значений l₁,...,l_M , и несущественного параметра a

s_i(t; a)=s(t; l_i,a); i=1, . . . , M. (4.10.17)

Полагают известными детерминированные функции s₁( ), . . . , s_M( ) tи a, априорные вероятности P_i посылки каждого сигнала s_i, плотность вероятности несущественного параметра p(a) и статистику помехи n(t).

Требуется определить:

а) алгоритм оптимальной обработки принимаемых колебаний u(t), обеспечивающий наименьшую среднюю вероятность ошибочных решений Р_ош.ср. (или наибольшую среднюю вероятность правильных решений Р_{прав.ср.}),

б) расчетные выражения для качества оптимальной системы Р_ош.ср. (или Р_{прав.ср.}).

Чтобы каким-либо способом (не обязательно лучшим) принять одно из M допустимых в настоящей задаче решений 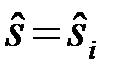(i=1,…,М) нужно каждому возможному значению вектора принимаемых колебаний - , поставить в соответствие одно из решений 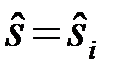(i=1,…,М). Следовательно, нужно разделить множество Uвсех возможных - значений принимаемого колебания на M областей U₁,...,U_M и решение принимать в соответствии с правилом:

если 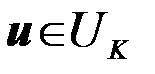, то 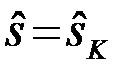. (4.10.18)

При определении оптимальной системы различения M сигналов удобно исходить из необходимости максимизировать среднюю вероятность правильных решений Р _{прав.ср.}=P₁Р _прав.1+ . . . + P_MР _прав.m

Аналитическое выражение для вероятности Р_прав.1 принятия правильного решения 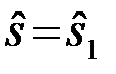при условии, что передается 1-й сигнал s=s₁ , определяется формулой

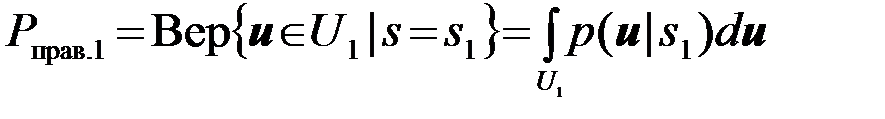, (4.10.19)

где p( |s₁) - условная плотность вероятности принятого колебания при условии, что был послан 1-й сигнал s=s₁ (функция правдоподобия 1-го сигнала).

Наша задача сводится к такому разделению множества U на области U₁ , . . . ,U_M , при котором максимизируется средняя вероятность правильных решений Р_{прав.ср.}:

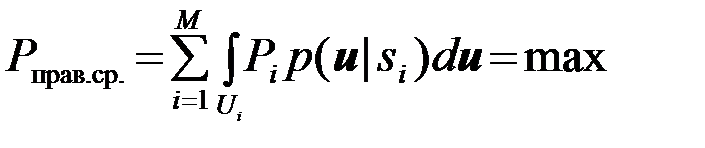(4.10.20)

которая связана со средней вероятностью ошибочных решений P_ош.ср. соотношением

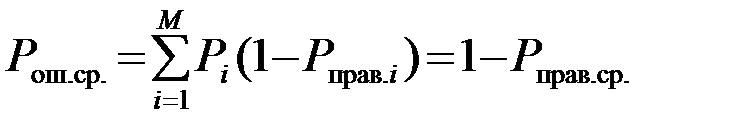. (4.10.21)

Входящая в (20) сумма интегралов 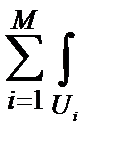сводится к интегрированию по всему пространству U. Для этой суммы можно записать:

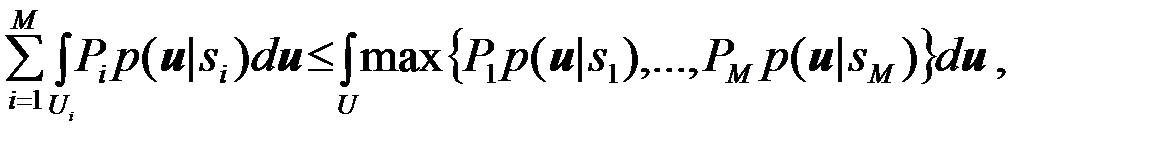(4.10.22)

где 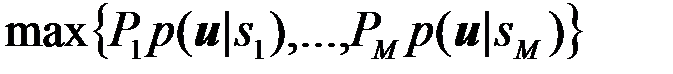- значение максимального (при данном ) числа 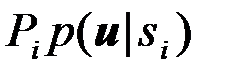, заключенного в скобки { }.

Знак равенства в (22), соответствующий условию Р_{прав.ср}=max, достигается только тогда, когда к области i-го решения U_iотносят все точки , для которых

.

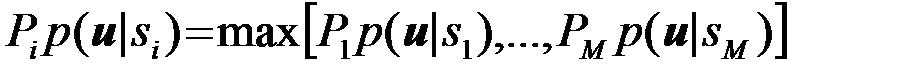Только в этом случае подинтегральная функция в левой части (22), в каждой точке пространства U, по которому ведется интегрирование, будет иметь максимально возможное значение. Соответственно максимально возможное значение будет иметь вероятность Р_{прав.ср.}

Таким образом, получаем следующий алгоритм принятия оптимального решения. Принимается решение о наличии k-го сигнала 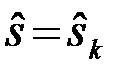, если

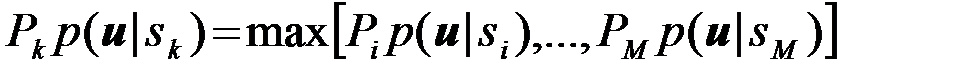. (4.10.23)

т.е. если удовлетворяется система из M-1неравенства

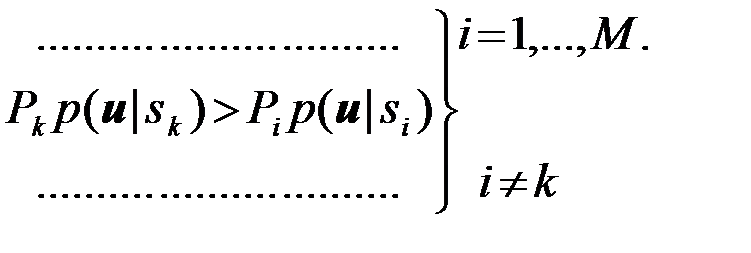(4.10.24)

Система оптимальной обработки должна сформировать по наблюдению {u(t),tÎ(0,T)}M чисел 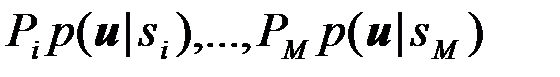, сравнитьих между собой и выбрать наибольшее. Правило решения кратко будем записывать так

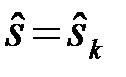, если 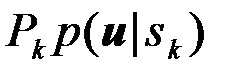=max. (4.10.25)

Если все сравниваемые величины 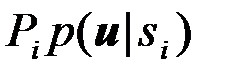разделить на безусловную ПВ вектора наблюдений получим, что формировать и сравнивать между собой можно апостериорные вероятности различных сигналов

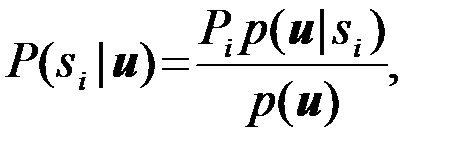i=1,…,M.

Соответствующее оптимальное правило решений

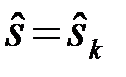, если 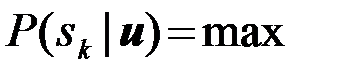(4.10.26)

называют решением по максимуму апостериорной вероятности (МАВ).

Наконец, часто априорные вероятности всех различаемых сигналов можно считать примерно одинаковыми P₁=,...,=P_M=1/M. При этом оптимальное решение принимается по максимуму функции правдоподобия

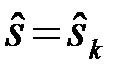, если . (4.10.27)

и называется решением по максимуму правдоподобия (МП).

Подробно изученные нами системы различения двух сигналов являются частным случаем систем различения M сигналов. Отличие состоит только в числе каналов. Так, например, оптимальная система различения M равновероятностных (P₁=,...,=P_M=1/M) полностью известных сигналов s_i(t),...,s_M(t) с одинаковыми энергиями Э_i=,...,=Э_M=Э должна принимать решение по максимуму функции правдоподобия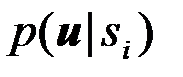

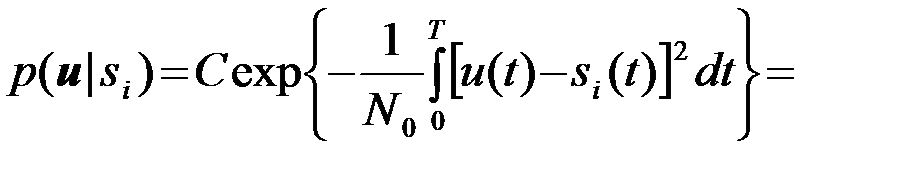
(4.10.28)

Множитель, заключенный в скобки { }, одинаковый для всех s_i . Поэтому решение можно принимать по максимуму корреляционного интеграла Y_i ;

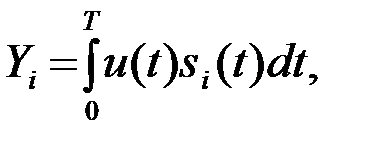i=1,…,М. (4.10.29)

т.е. придерживаться правила:

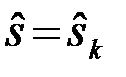, если Y_k=max. (4.10.30)

Оптимальная система (рис.4.25) по принятому колебанию должна формировать корреляционные интегралы с образцами всех ожидаемых сигналов s₁(t),...,s_M(t). На рис.4.25 процедура эта выполняется методом корреляции. Число каналов обработки принимаемого колебания u(t) в общем случае равно числу различаемых сигналов M. Значения корреляционных интегралов Y_i поступают в схему выбора (Сх.выб), которая принимает решение в соответствии с правилом (30). Схема рис.4.25 может быть использована, в частности, для оптимального когерентного приема ФМШС. Если неизвестны начальная фаза или начальная фаза и интенсивность принимаемых сигналов, то в соответствии с доказанным в §4.9 оптимальная система вместо корреляционного интеграла Y_iдолжнаформировать модульное значение комплексного корреляционного интеграла Z_i принимаемого колебания u(t) с образцами всех сигналов 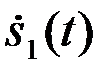,…, , 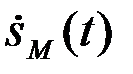которые могут поступить на вход системы

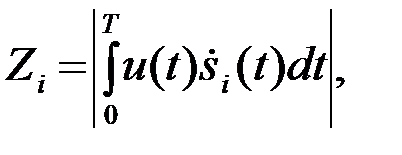i=1,…,М , (4.10.31)

причем начальные фазы j_i и интенсивность (множитель K одинаковый для всех каналов) образцов 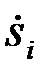выбираются произвольно.

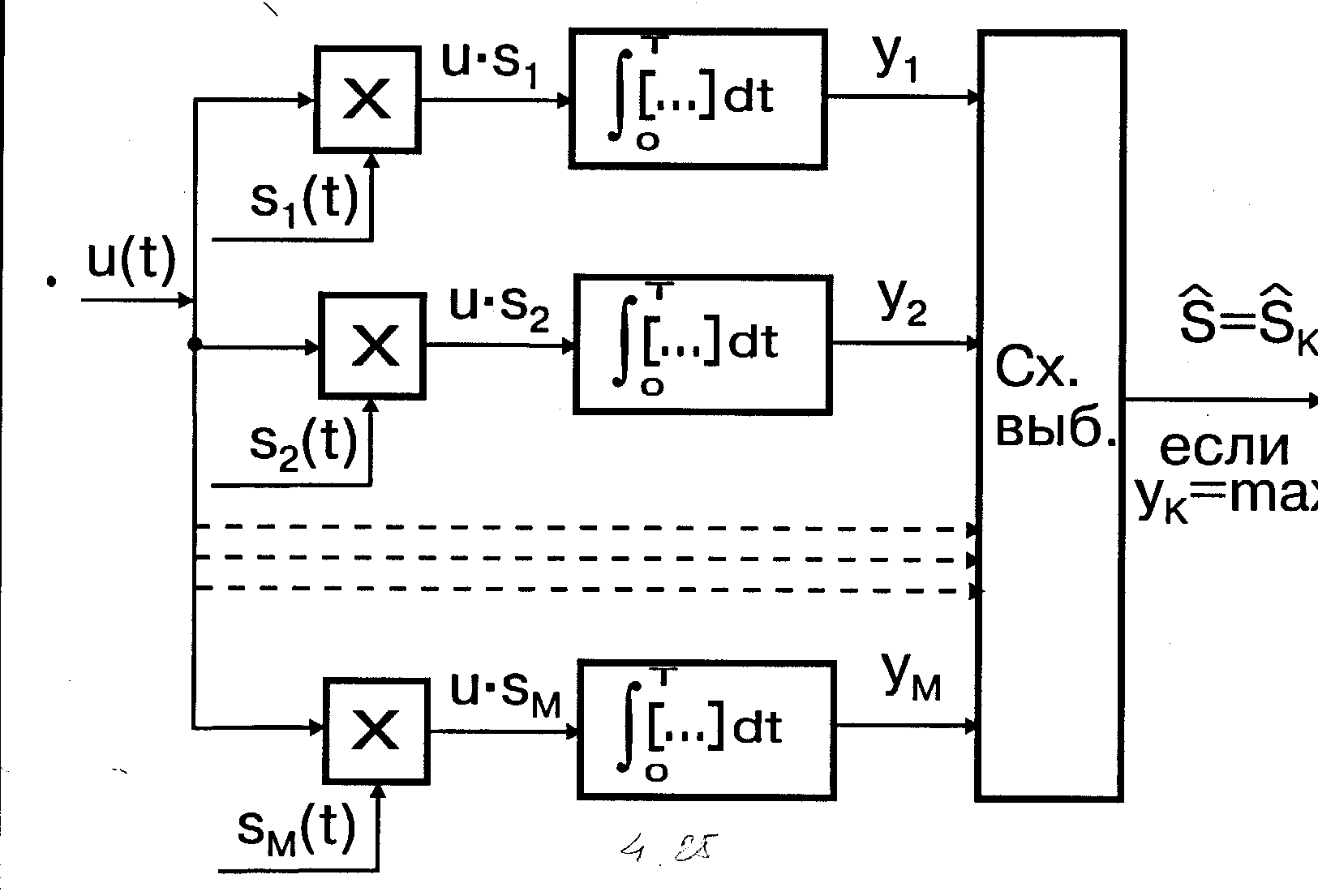
Рис. 4.25

Принимается решение

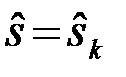, если Z_k=max. (4.10.32)

На рис. 4.26 приведена оптимальная схема различения M сигналов с одинаковыми энергиями и с неизвестными начальными фазами (или с неизвестными начальными фазами и интенсивностями), выполненная с использованием метода оптимальной фильтрации. Импульсные характеристики оптимальных фильтров (ОФ) согласовываются с полезными сигналами с точностью до произвольных начальной фазы j_i и масштабного множителя K:

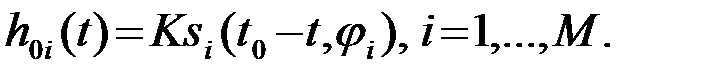
Все детекторы Д имеют одинаковые амплитудные характеристики. От системы синхронизации на схему выбора подаются тактовые импульсы, фиксирующие моменты времени t₀ , в которые должно производиться сравнение выходных напряжений U_Дi(t₀),i=1,...,M.

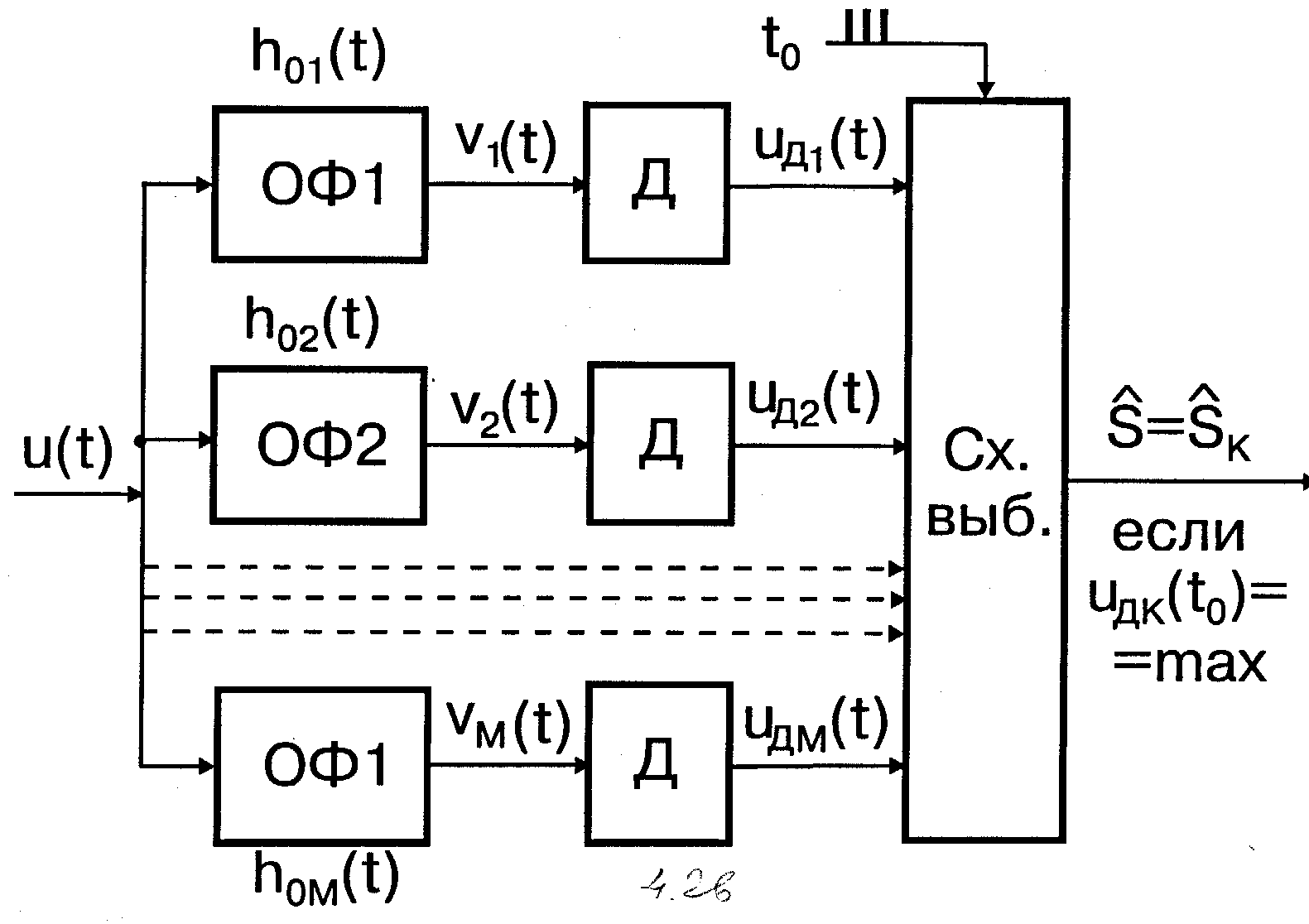
Рис. 4.26

4.10.4. Расчет качества оптимальной системы различения M сигналов.Полагаем, что все сигналы s₁, . . . , s_M имеют одинаковые априорные вероятности P₁=, . . . ,=P_M и одинаковые энергии Э₁=, . . . ,=Э_M =Э. В этих условиях оптимальные алгоритмы различения для полностью известных сигналов и для сигналов с неизвестной начальной фазой определены формулами (30) и (32). Схема расчета и результирующая расчетная формула, которая будет получена, для этих двух случаев совпадает. В практических ситуациях чаще встречается различение сигналов с неизвестной начальной фазой. Поэтому приведем расчет Р_{прав.ср.} при различении некогерентных сигналов. Начнем с расчета условной вероятности правильного различения Р_прав.1 при условии, что послан сигнал s₁, т.е. вероятность того, что при условии s=s₁(u=s₁+n) удовлетворяется система (M-1) неравенства {Z₁ >Z_i , i=2,…,M}

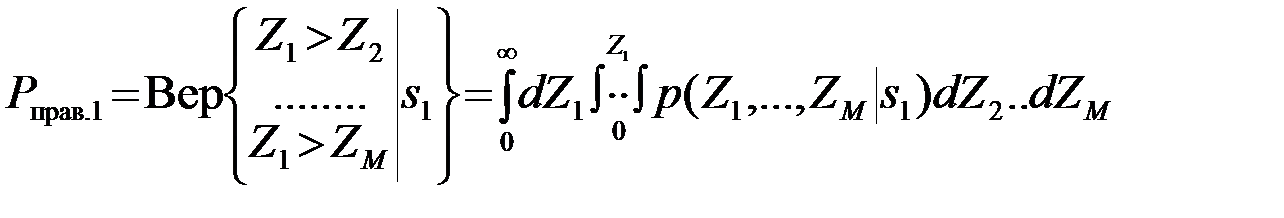. (4.10.33)

В (33) 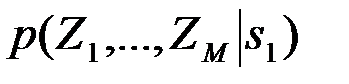условная (обусловлено событие s=s₁) совместная ПВ величин Z₁,…,Z_M, а интегрирование ведется в пространстве Z₁, …,Z_M Î (0,¥) по области {Z₁>Z_i,i=2,…,M,Z₁Î(0,¥)}. Далее вводится еще одно ограничительное условие. Все сигналы s₁,…,s_M полагаются (как, например, ФМШС при M>>1) практически взаимно ортогональными в усиленном смысле

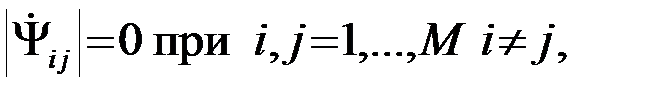(4.10.34)

что позволяет сделать два существенных упрощения. Во-первых, все сигналы становятся симметричными - имеют одинаковые априорные вероятности, э