Расчет качественных показателей оптимальной системы различения двух сигналов со случайной начальной фазой

Расчет теоретически предельного качества различения двух сигналов с неизвестной начальной фазой проведем для двух основных случаев.

4.8.1. Различение нулевого и ненулевого сигналов. Нужно рассчитать вероятность ошибочных решений Р_ош1 и Р_ош2 в оптимальной системе при передаче первого (ненулевого) и второго (нулевого) сигналов. Вероятность Р_ош1 согласно алгоритму (4.6.19) - это вероятность удовлетворения неравенства Z<0.5Э при условии, что передается ненулевой сигнал (u=s+n)

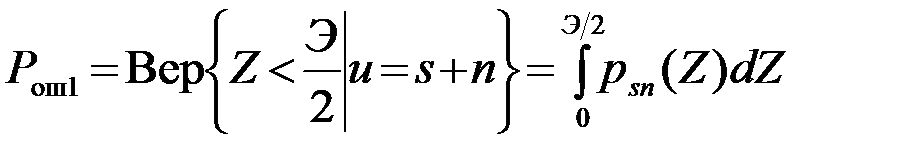
(4.8.1)

где 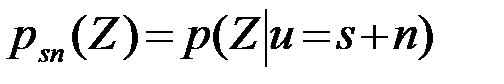- ПВ величина 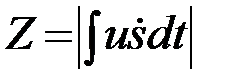при условии, что u=s+n.

Аналогично

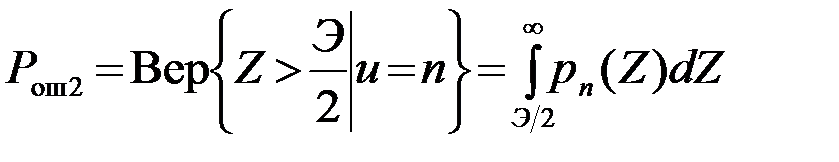(4.8.2)

где P_n(Z)=P(Z|u=n)-ПВ величины Z при условии, что u=n.

Задача фактически сводится к определению двух ПВ P_sn(Z) и P_n(Z) модульного значения комплексного корреляционного интеграла Z:

при u=s+n

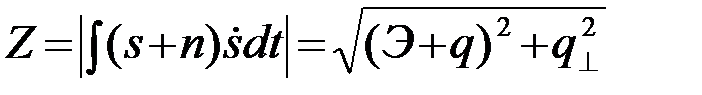(4.8.3)

и при u=n

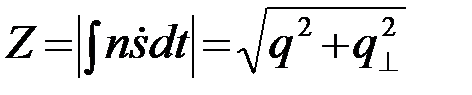, (4.8.4)

где

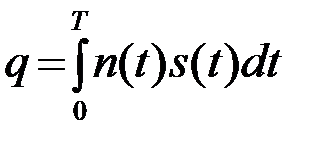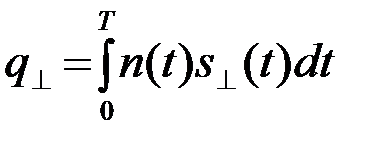, . (4.8.5)

В п.4.5.1 было показано, что величины q и q_^ являются нормальными центрированными случайными величинами с дисперсией s_q²=0.5N₀Э, т.е.q, q_^®N(0,s_q²=0.5N₀Э). Кроме того, покажем, что нормальные случайные величины q и q_^ некоррелированные (следовательно, независимые)

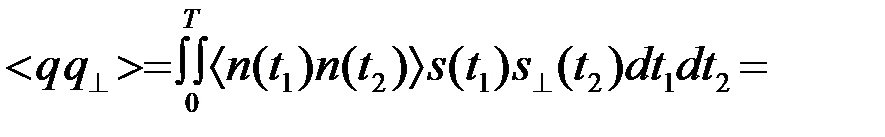
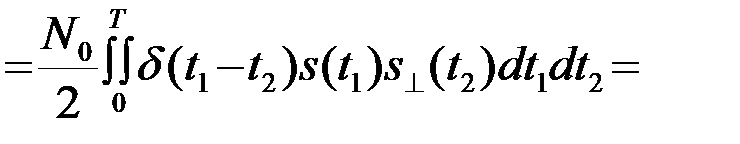
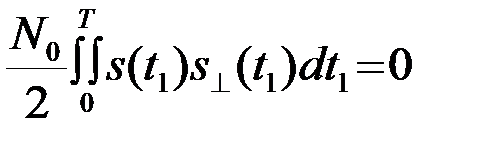, (4.8.6)

так как сопряженные (по Гильберту) сигналы s и s_^ ортогональны.

Модуль комплексного корреляционного интеграла Z , является корнем квадратным из суммы квадратов двух независимых гауссовских величин с одинаковыми дисперсиями s_q². В одном случае (4) эти величины центрированные, в другом (3) могут иметь отличное от нуля математическое ожидание. Плотность вероятности такой величины (Z) часто встречается в практических приложениях теории вероятности. Приведем в качестве примера расчет интересующих нас ПВ.

Пример 4.8.1. Положим х₁ и х₂ независимые гауссовские величины с одинаковыми дисперсиями s_q² и с математическими ожиданиями е₁ и е₂

x₁=e₁+q₁®N(e₁ ,s_q²), x₂=e₂+q₂®N(e₂ ,s_q² ), (4.8.7)

Требуется определить ПВ p_Z(Z)величины 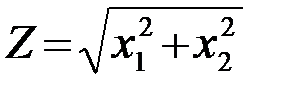. Перейдем к новым переменным (к полярным координатам)

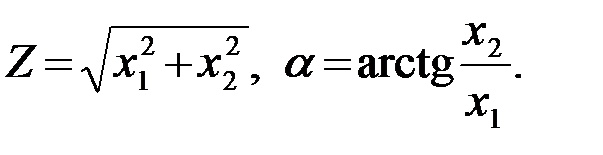(4.8.8)

Обратный переход (к декартовым координатам)

x₁ = Zcosa, x₂ = Zsina, 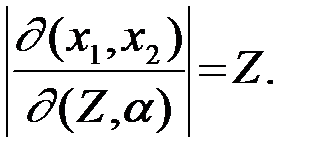(4.8.9)

Преобразование переменных х₁и х₂ , а также их математических ожиданий е₁ и е₂, в полярные координаты иллюстрируется на рис.4.18. Совместная ПВ х₁и х₂

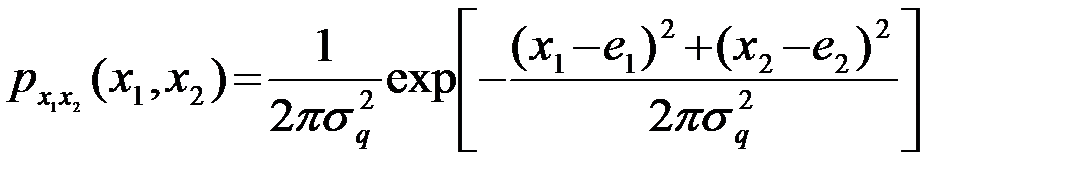. (4.8.10)

Совместная ПВ Z и a(Э²=е₁² + е₁², е₁=Эcosb,е₂=Эsinb).

,

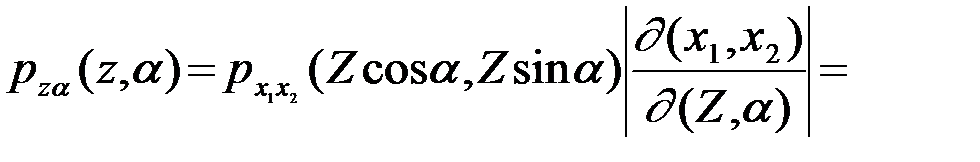
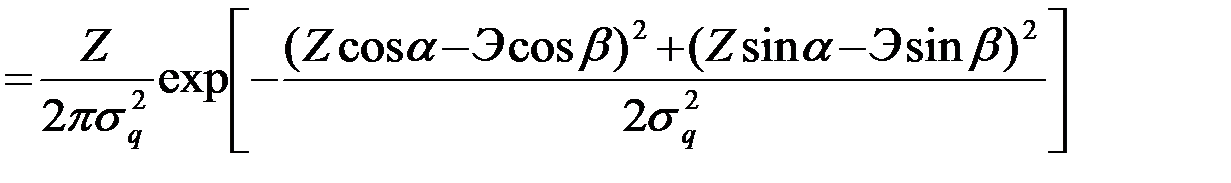откуда

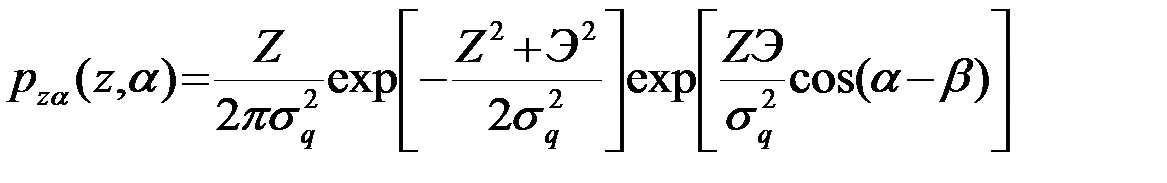. (4.8.11)

Требуемая ПВ p_Z(Z)

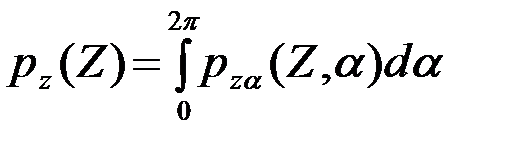
после усреднения (11) по a, принимая во внимание (4.6.12), получается равной

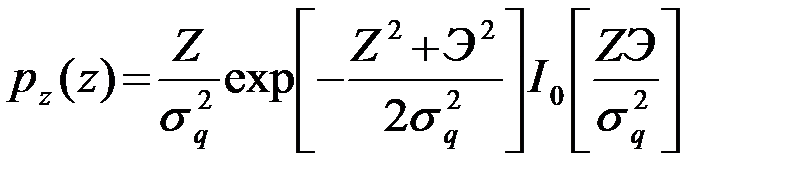. (4.8.12)

и называется обобщенным распределением Релея или распределением Релея- Райса.

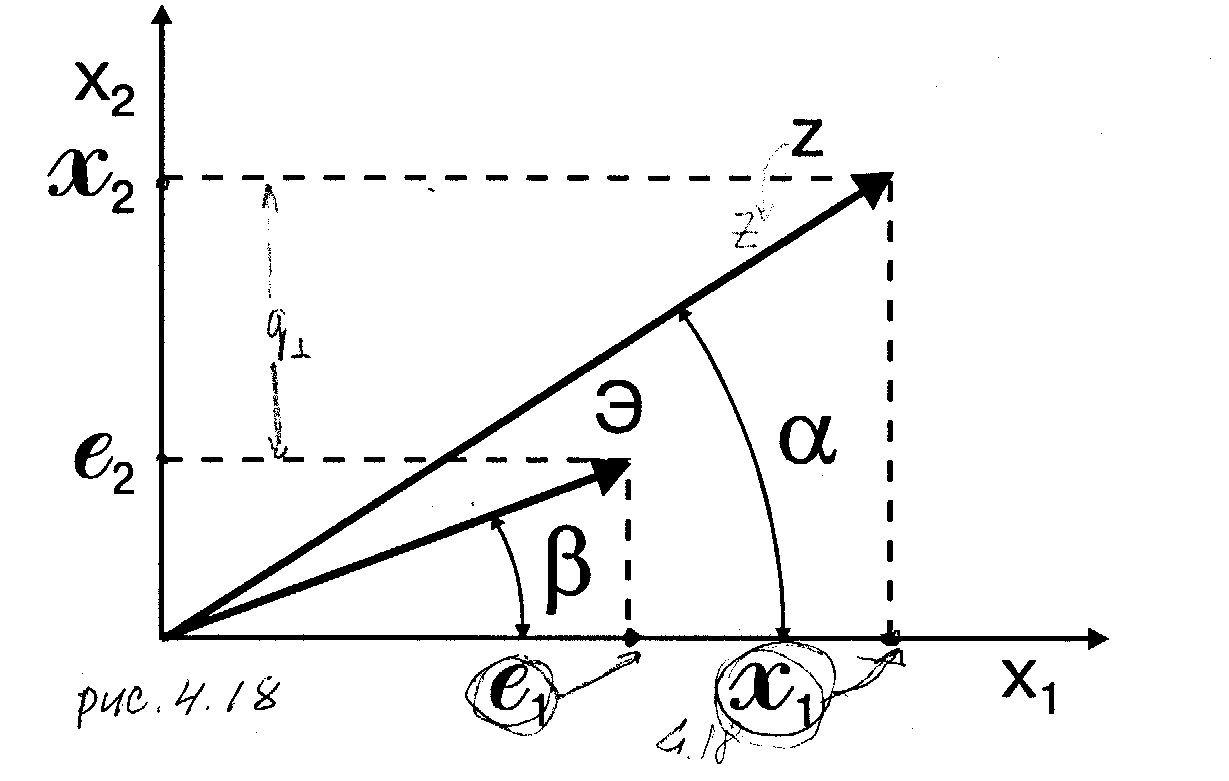
Рис. 4.18

В частном случае, когда е₁=е₂=0(Э=0) и случайные величины х₁ и х₂являются независимыми центрированными величинами с одинаковыми дисперсиями s_q² , полярные координаты Z и a оказываются независимыми случайными величинами

p_Za(Z,a)=p_Z(Z)p_a(a) ,

распределенными: Z - по закону Релея, a - равновероятно

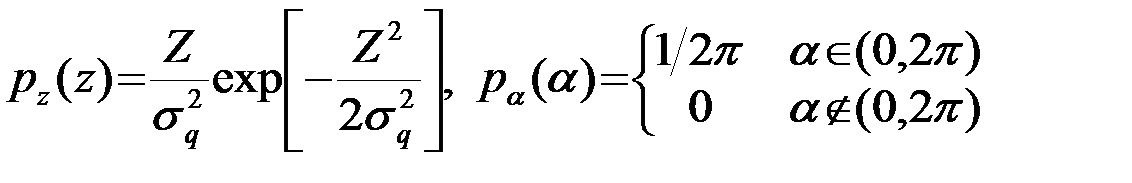. (4.8.13)

Наоборот, при переходе от полярных координат Zи a, являются независимыми величинами с распределением (13), к декартовым координатам x₁иx₂, последние оказываются независимыми гауссовскими центрированными величинами с одинаковыми дисперсиями s_q²: x₁, x₂®N(0,s_q²), .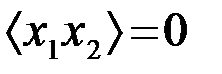

Распределение Релея - Райса (12) при различных значениях отношения Э/s_q от 0 до 5 изображено на рис.4.19. При увеличении параметра Э/s_q распределение (12) асимптотически стремится к нормальному N(Э,s_q²).

В решаемой нами задаче случайная величина (3) совпадает с величиной Z при условии, что е₂=0,b=0,e₁=Э, а величина (4) при условии, что e₁=е₂=0,Э=0. При этом ПВ p_sn(Z) и p_n(Z), определяющие вероятности ошибок (1) и (2), выражаются формулами (12) и (13) соответственно. В результате вероятности ошибок Р_ош2 и Р_ош1 после замены переменной интегрирования Z/s_q=x получаются равными:

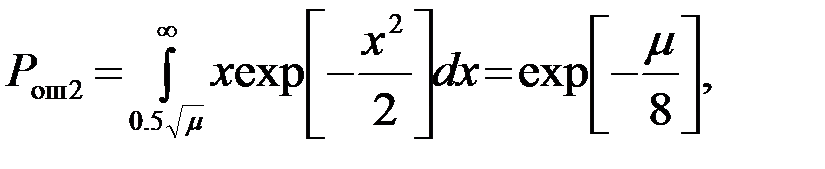(4.8.14)

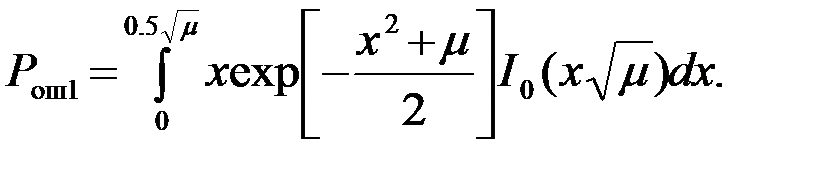(4.8.15)

Интеграл (15) выражается через табулированную функцию *)

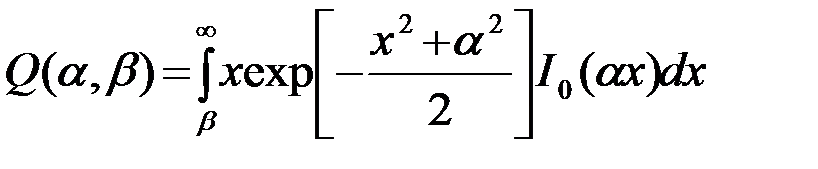. (4.8.16)

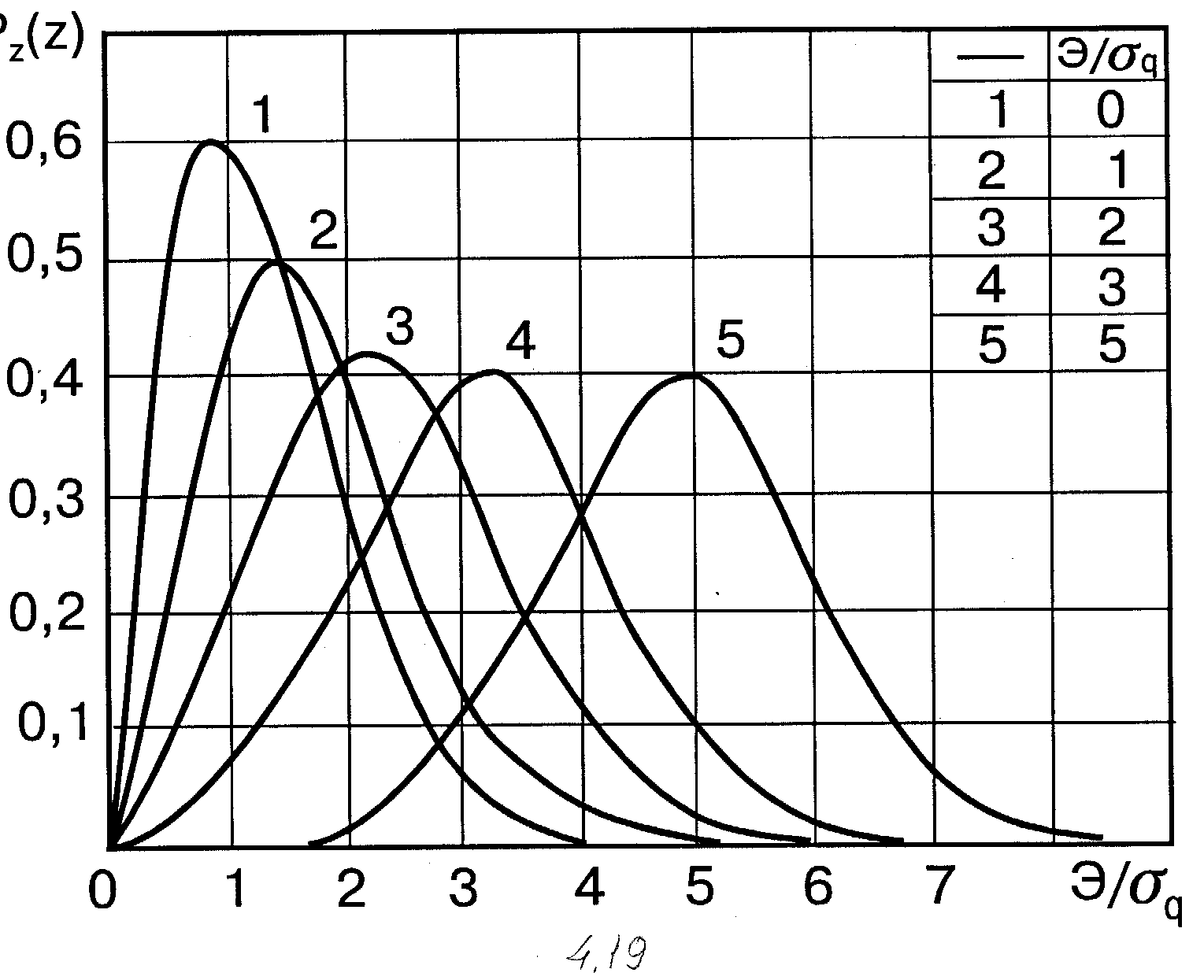
Рис. 4.19

В результате, принимая во внимание, что Q(a,0)=1, имеем

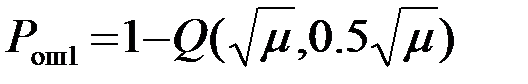(4.8.17)

P_ош.ср = 0.5(P_ош1 + P_ош2 ) . (4.8.18)

Приведенными формулами можно пользоваться при m>>1, когда Z_п»0.5Э, например, при расчете энергии минимально различимого сигнала Э_cmin .

4.8.2. Различение сигналов с одинаковыми энергиями. В этом случае

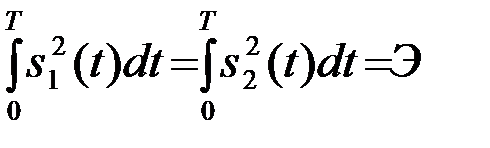, (4.8.19)

кроме того, задается степень коррелированности сигнала s₁с сигналами s₂ и s_2^ (или с аналитическим сигналом ):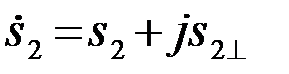

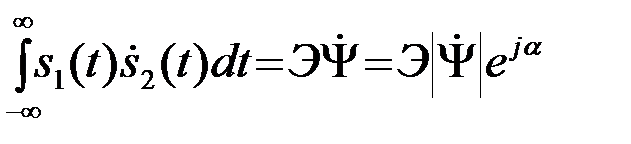(4.8.20)

или

,

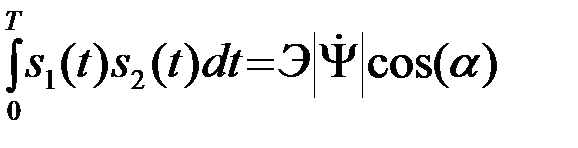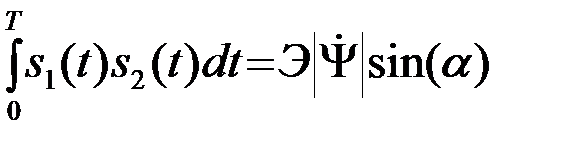, (4.8.21)

где 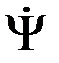- комплексный коэффициент корреляции сигналов s₁ и s₂

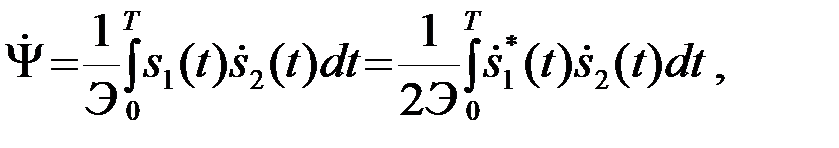(4.8.22)

а | 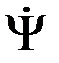| и a-его модуль и аргумент.

В рассматриваемой системе различения (Э₁=Э₂) достаточно рассчитать условную вероятность ошибок Р_ош1 при передаче сигнала s₁. Вероятность Р_ош2, а также средняя вероятность ошибок Р_ош.ср. совпадают по величине с Р_ош1=Вер{Z₁<Z₂|u=s₁+n}.

При условии, что u=s₁+n

Z₁= =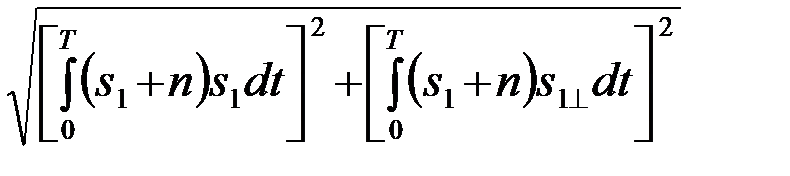

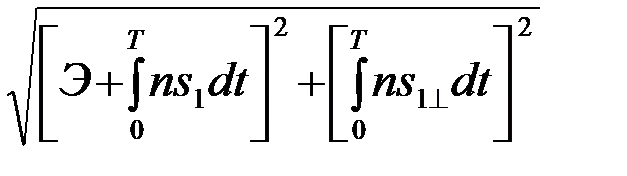= (4.8.23)

и

Z₂= 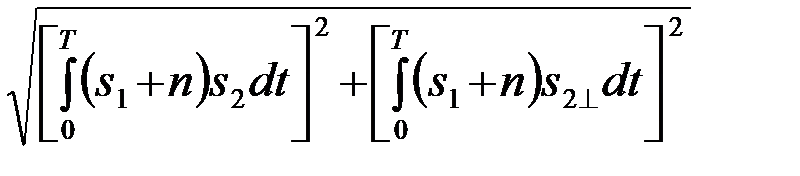= (4.8.24)

= .

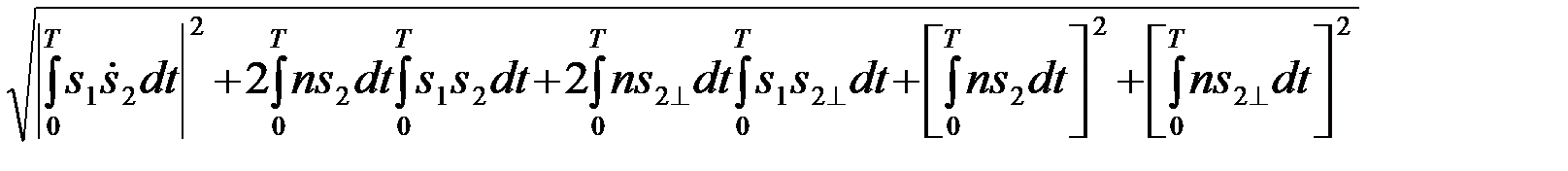Точный расчет Вер{Z₁<Z₂|u=s₁+n} приводит к громоздким вычислениям, а результат получается в плохо обозримом виде [ ]. Мы ограничимся приближенным расчетом в предположении что между сигналами s₁ и s₂ имеется заметная корреляция 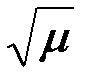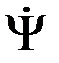|>З, а также точный расчет для случая ортогональных сигналов | 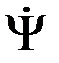| =0.

При условии, что 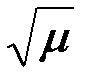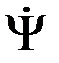>З ,m>>1(Э>>N₀ /2) и, учитывая (21),

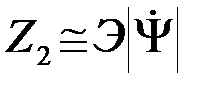
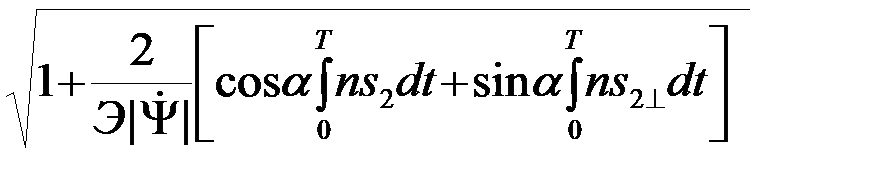. (4.8.26)

Второе слагаемое под знаком радикала в (26) мало (его среднеквадратическое значение2/( 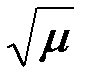| |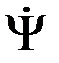)<1).Поэтому можно воспользоваться формулой 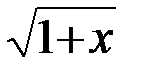»1+0,5x. Это дает

Z₂ @ Э| 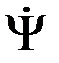|+cosa 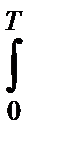ns₂dt +sina 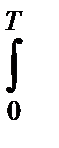ns_2^dt (4.8.27)

и вероятность Р_ош1 = Вер{Z₁<Z₂|u=s₁+n} получается равной

P_ош1= Вер 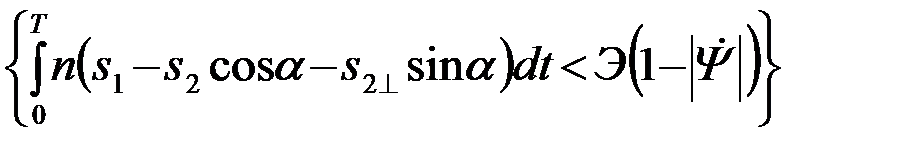. (4.8.28)

Функцию, заключенную в скобки ( ) в (28), обозначим

s_экв(t)=s₁(t)- s₂(t)cosa - s_2^(t)sina (4.8.29)

и рассчитаем энергию эквивалентного сигнала s_экв(t)

Э_экв= 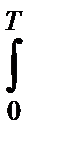s²_экв(t)dt= 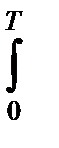[s₁(t)- s₂(t)cosa - s_2^(t)sina]² dt .

Учитывая (21) и ортогональность квадратурных сигналов, получаем

Э_экв=2Э(1-| 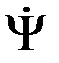|), (4.8.30)

что позволяет вероятность Р_ош1 представить в виде

Р_ош1=Вер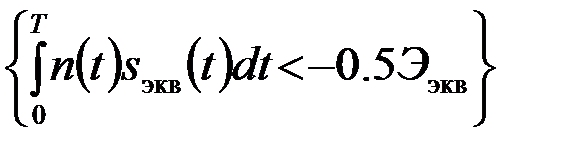

и свести задачу к типовому случаю (4.5.5). Таким образом, при различении коррелированных сигналов

Р_ош.ср. =Р_ош1 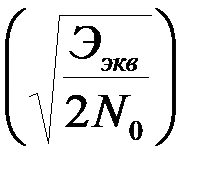@ 1-Ф = 1-Ф 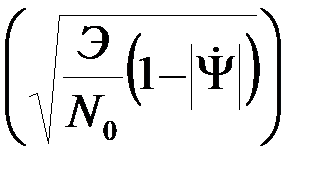. (4.8.31)

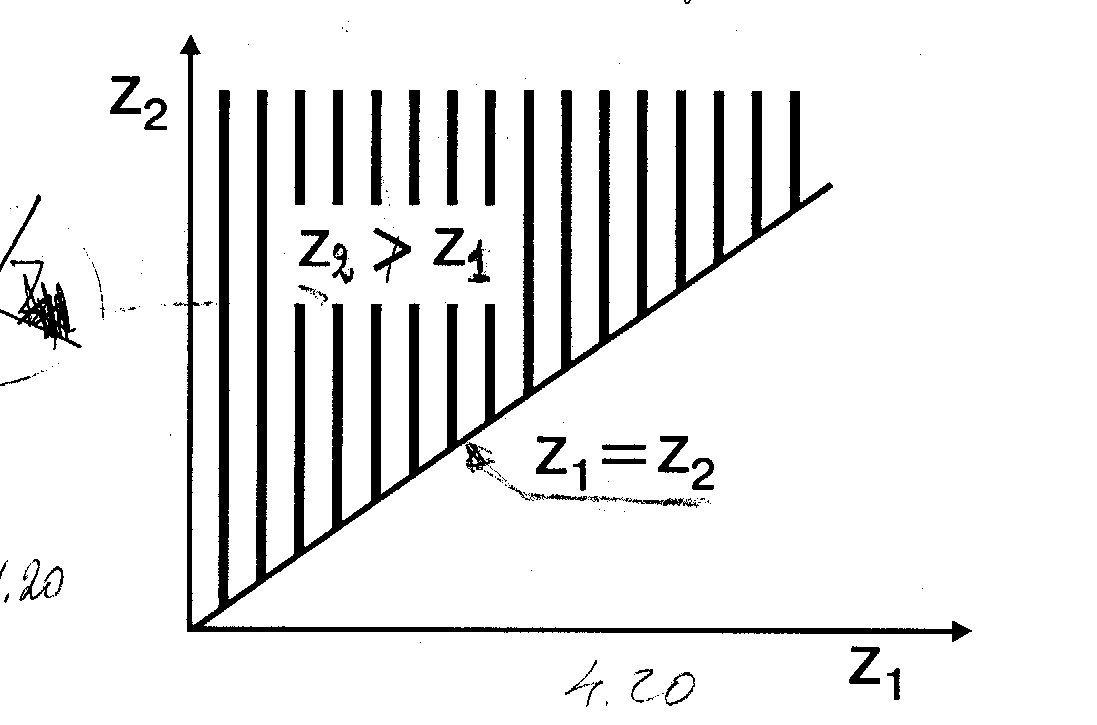
Рис. 4.20

При некоррелированных сигналах s₁и s₂, когда | |=0 или

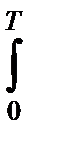s₁s₂dt = 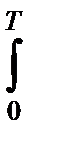s₁s_2^dt = 0, (4.8.32)

формулы (23) и (24) для модульных значений корреляционных интегралов Z₁и Z₂(при условии, что u=s₁+n) принимают вид :

Z₁= 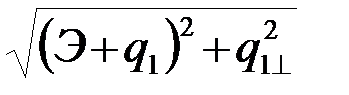, (4.8.33)

Z₂= 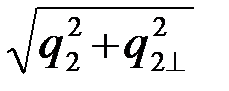, (4.8.34)

q_i= 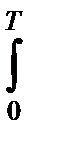n(t)s_i(t)dt, q_i^= 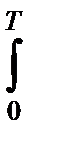n(t)s_i^(t)dt, i=1, 2 . (4.8.35)

Случайные величины Z₁ и Z₂ совпадают по своей структуре с величинами (3) и (4), а их ПВ 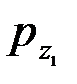(Z₁)=p_sn(Z₁) и 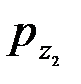(Z₂)=p_n(Z₂) - с ПВ (12) и (13). Кроме того, случайные величины Z₁и Z₂ независимы, так как попарно независимы входящие в них нормальные величины q₁, q_1^, q₂, q_2^. Например,

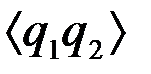
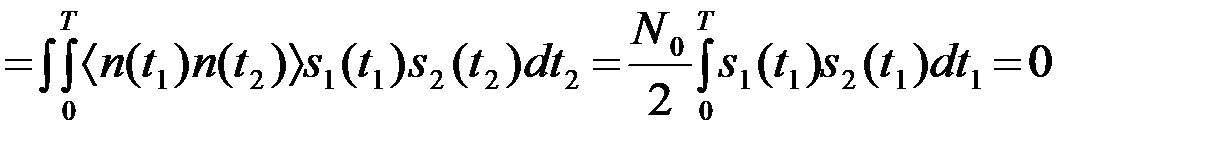. (4.8.36)

Аналогично

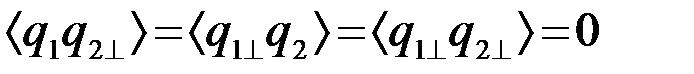. (4.8.37)

Вероятность Р_ош1 равна вероятности удовлетворения неравенства Z₁<Z₂ при условии u=s₁+n, что выражается интегралом ПВ Р₂(Z₁,Z₂|s₁) = P_sn(Z₁)P_n(Z₂) по области, заштрихованной на рис. 4.20, в которой удовлетворяется неравенство Z₁<Z₂.

P_ош1= dZ₁ P₂(Z₁,Z₂)dZ₂= P_sn(Z₁)dZ₁ P_n(Z₂)dZ₂=

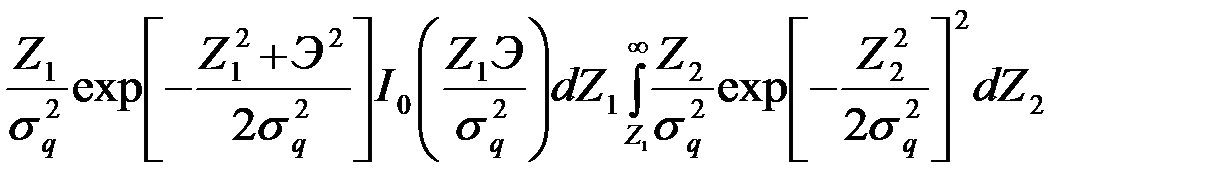= . (4.8.38)

Интеграл по Z₂, входящий в (38), равен exp[-Z₁²/(2s_q²)]. Выражение, получившееся после интегрирования по Z₂, запишем в виде

,

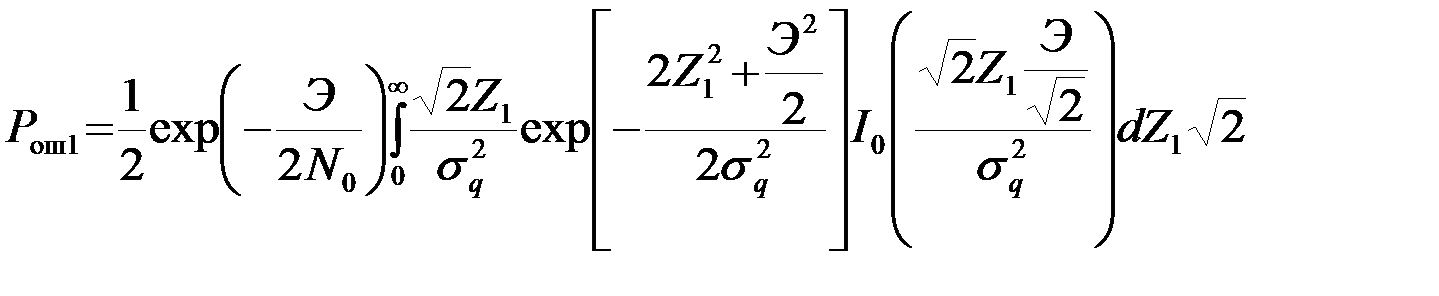в котором под интегралом стоит ПВ Релея-Райса случайной величины 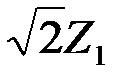, с параметрами s_q² и Э²/2. Интеграл равен 1, так как берется по всем возможным значениям случайной величины 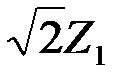. Поэтому

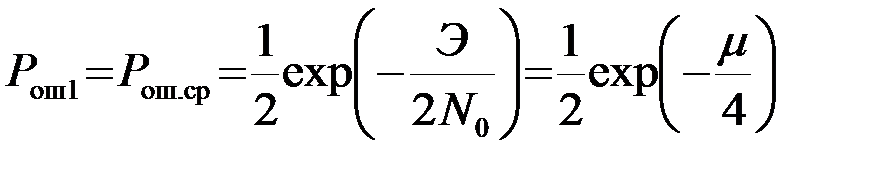. (4.8.39)