Схемные методы формирования модульного значения комплексного корреляционного интеграла

При приеме сигналов с неизвестной начальной фазой, как и при приёме полностью известных сигналов, имеются две практические возможности реализации оптимальных схем обработки наблюдений - это использование метода корреляции и метода оптимальной фильтрации.

4.7.1. Метод корреляции. При использовании этого метода непосредственно моделируется выражение для модуля комплексного корреляционного интеграла Z, представленного в следующем виде

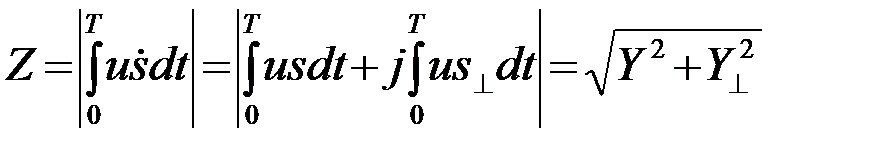. (4.7.1)

где Y и Y_^

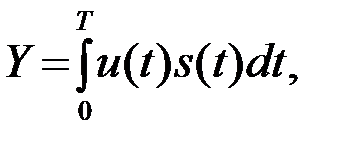
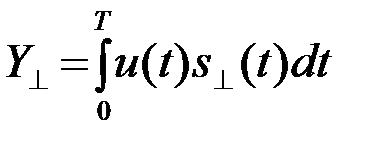(4.7.2.)

корреляционный интеграл u с sи квадратурный корреляционный интеграл u с s_^. На рис. 4.14 приведена структурная схема устройства.

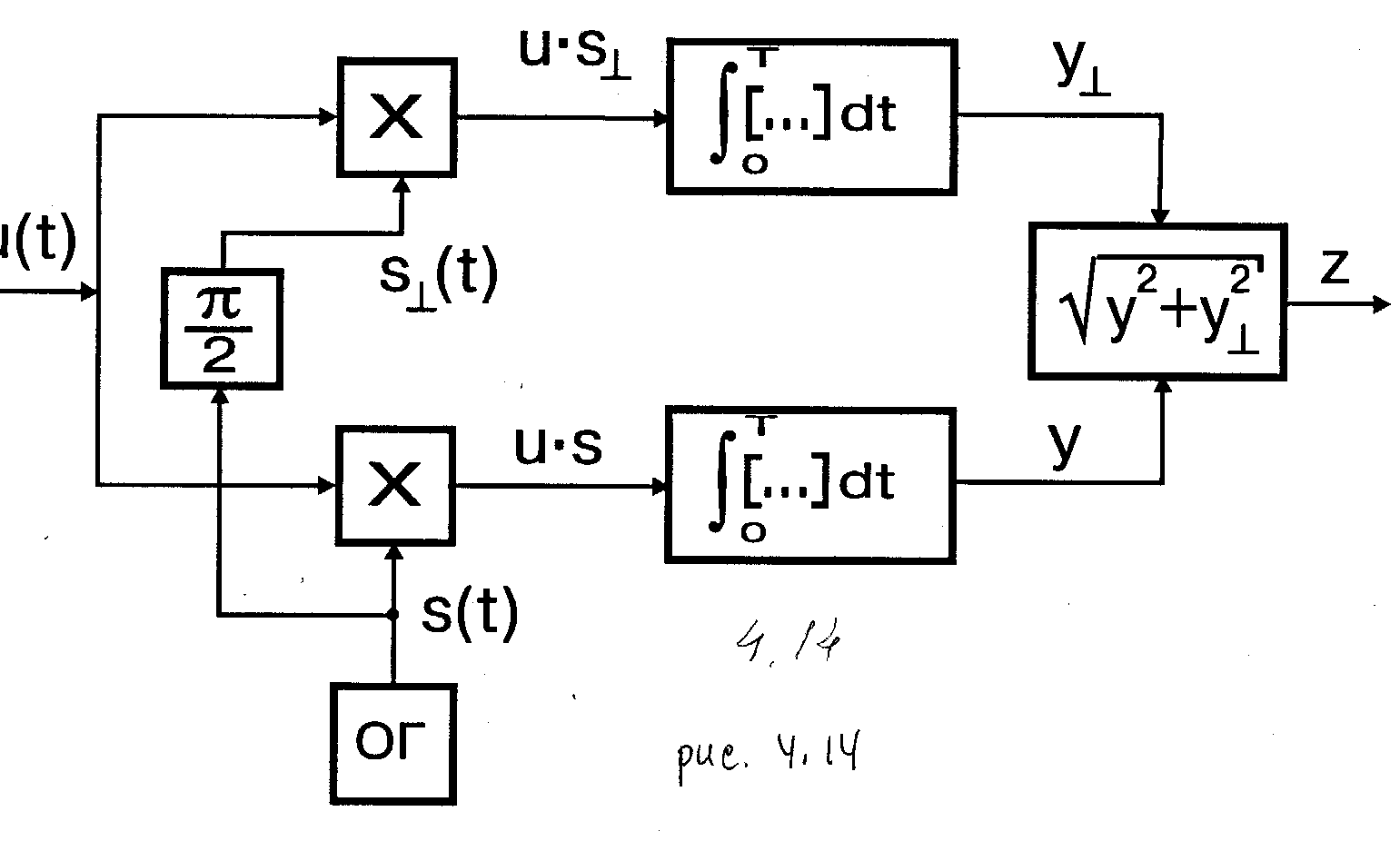
Рис. 4.14

Схема включает в себя следующие элементы: опорный генератор (ОГ), создающий на приемной стороне образец ожидаемого сигнала s(t); устройство p/2, сдвигающее фазу подводимых к нему колебаний на p/2 и формирующее, следовательно, квадратурный сигнал s_^(t); перемножающие устройства (x), интеграторы, осуществляющие интегрирование подводимых к ним колебаний на интервале наблюдения tÎ(0,T) и формирующие корреляционные интегралы Y и Y_^ , квадратор, осуществляющий операцию 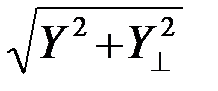над подводимыми к нему величинами и формирующий на своем выходе модульное значение комплексного корреляционного интеграла Z.

Приведенная схема не чувствительна к произвольному сдвигу начальной фазы ОГ. Положим ОГ вместо сигнала s(t) генерирует сигнал 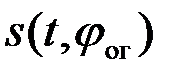, отличающийся от s(t) произвольным сдвигом фазы 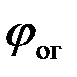. При этом схема рис. 4.14 будет формировать следующий выходной эффект

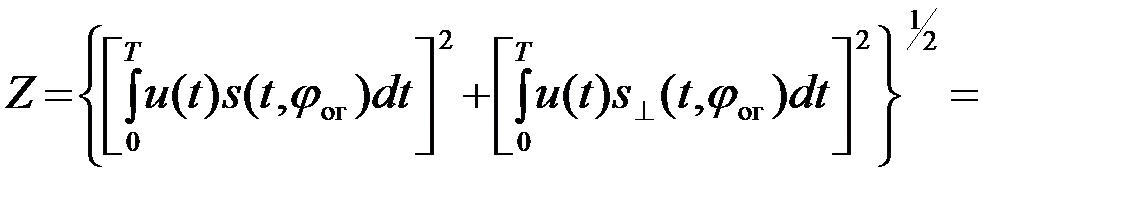
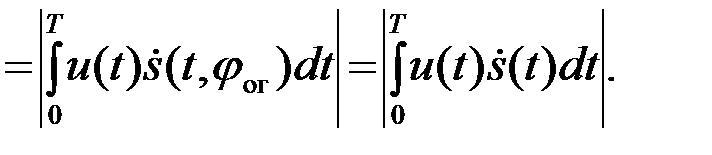(4.7.3)

При операции взятия модуля комплексного корреляционного интеграла начальная фаза сигнала исключается. Поэтому колебание ОГ 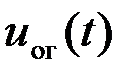должно быть согласовано с ожидаемым сигналом s(t,j) с точностью до произвольных начальной фазы 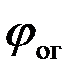и масштабного множителя K, характеризующего усиление

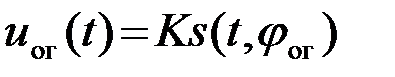(4.7.4)

Наличие в принимаемом сигнале неизвестной начальной фазы приводит к необходимости добавления в корреляционную схему оптимальной обработки квадратурного канала, формирующего Y_^ и квадратора. При различении двух сигналов s₁ и s₂ оптимальная система различения должна включать в себя два канала рассмотренного вида, формирующих

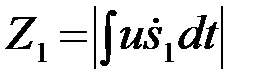и .

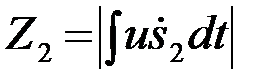4.7.2. Метод оптимальной фильтрации. Структурная схема оптимальной фильтровой обработки сигналов с неизвестной фазой приведена на рис. 4.15. Схема состоит из оптимального фильтра, изученного в п.4.4.2, и амплитудного детектора Д.

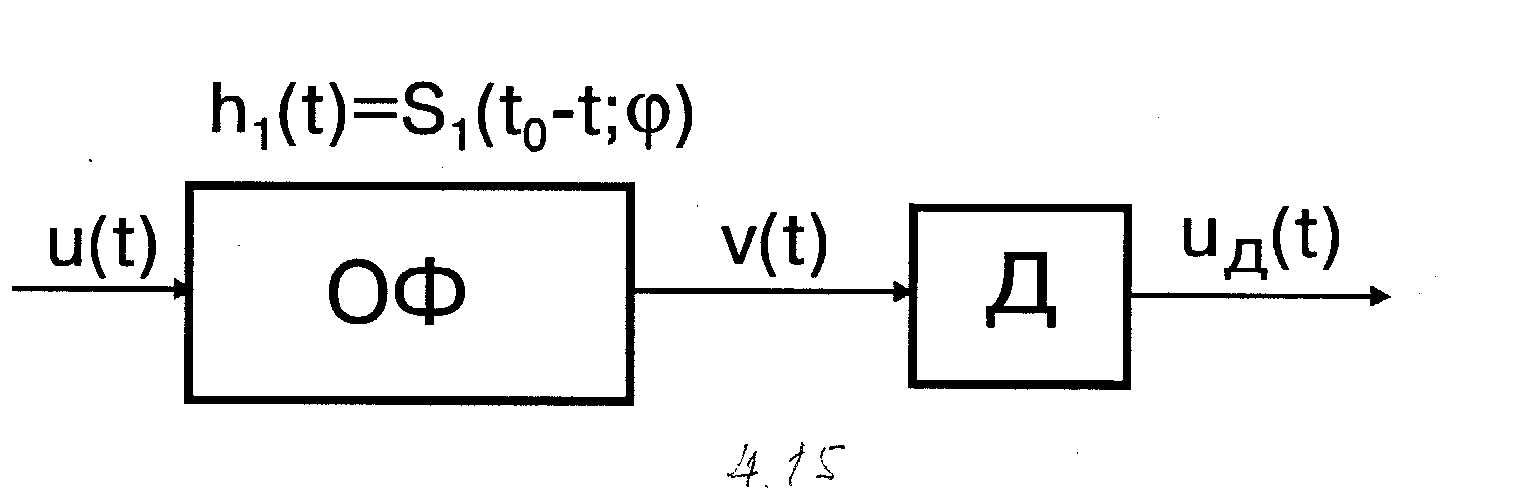
Рис. 4.15

Напряжения на входе и выходе ОФ, как и ранее, обозначены u(t) и υ(t), причем

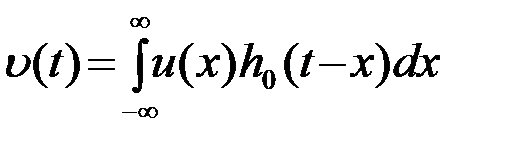(4.7.5)

где h₀(t) - импульсная характеристика ОФ, которая согласуется с ожидаемым сигналом с точностью до произвольной начальной фазы

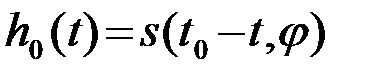или 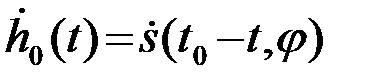. (4.7.6)

Напряжение на выходе детектора 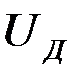, воспроизводит огибающую подводимых к нему колебаний 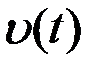и может быть представлено в следующем виде

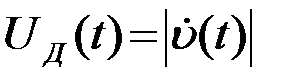.(4.7.7)

Остается записать комплексное выражение для выхода ОФ

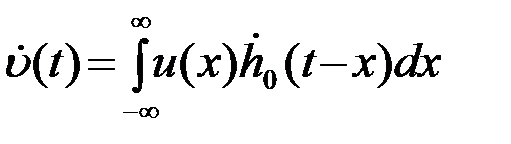. (4.7.8)

Действительно, если подвергнуть преобразованию Гильберта (по t) правую и левую часть (5), то будем иметь

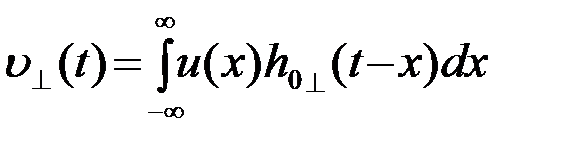, (4.7.9)

сложение u(t)+ju_^(t), т.е. (5) и (9), дает (8).

Окончательно выражение для выхода системы обработки 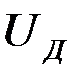с учетом (6) имеет вид

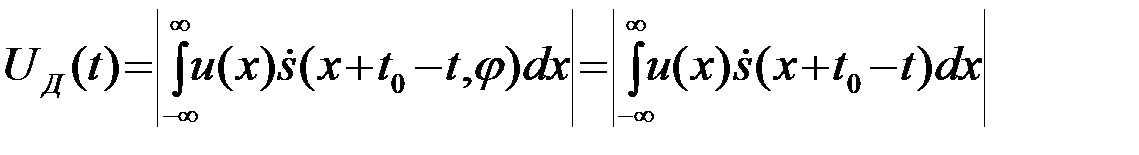. (4.7.10)

В момент t=t₀ система формирует модуль комплексного корреляционного интеграла

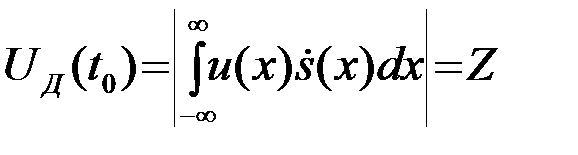. (4.7.11)

Таким образом, схема, изображенная на рис. 4.15, формирует в момент t=t₀ оптимальный выходной эффект Zи, следовательно, обеспечивает оптимальную обработку сигналов с неизвестной начальной фазой j, распределенной равновероятно. Наличие в принимаемом сигнале случайной начальной фазы привело к необходимости добавить в схему оптимальной фильтровой обработки амплитудный детектор. Другая особенность схемы состоит в том, что импульсная характеристика ОФ согласуется с сигналом с точностью до произвольной начальной фазы j.

На рис. 4.16 приведена структурная схема системы оптимального различения двух сигналов со случайными начальными фазами и с одинаковыми энергиями, в частности, сигналов КИМ ЧМ.

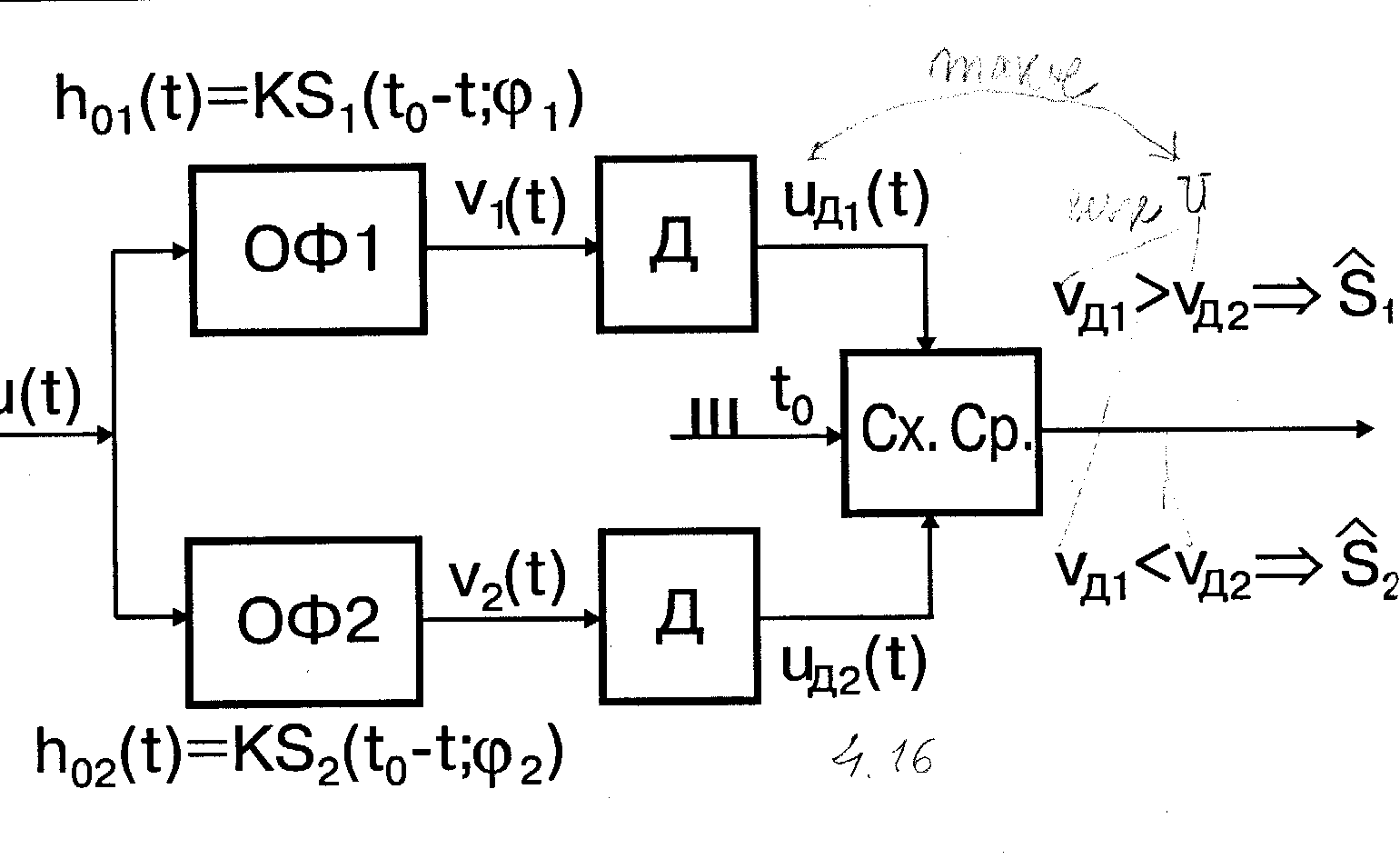
Рис. 4.16

Система имеет два канала с фильтрами ОФ₁ и ОФ₂, согласованными соответственно с первым s₁ и вторым s₂ сигналами. Импульсные характеристики оптимальных фильтров

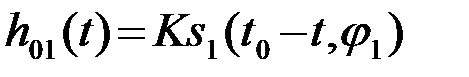и 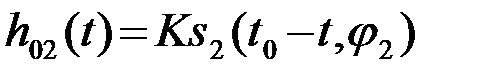. (4.7.12)

В момент t=t₀ напряжение на выходе детекторов Д₁ и Д₃ как было показано, воспроизводит модульное значение комплексных корреляционных интегралов

U_Д1(t₀ )=KZ₁, U_Д2(t₀ )=KZ₂. (4.7.13)

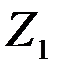
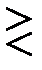
Система синхронизации (С) включает в момент окончания сигналов t=t₀ схему сравнения (СХ. СР.), в результате чего производится сравнение 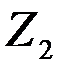и принимается оптимальное решение.

Заметим, вид детекторной характеристики 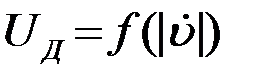в рассмотренной схеме значения не имеет при условии, что характеристики обоих детекторов идентичны и являются монотонно возрастающей функцией.

На рис.4.17 изображены эпюры напряжений u,u₁,u₂,U_Д1,U_Д2 в схеме рис.4.16 при прохождении последовательности из 4-х сигналов КИМ ЧМ без помех. Полагается, что сигналы s₁(t,j₁)иs₂(t,j₂)взаимно ортогональны (см. п. 4.8). Соответственно на выходе ОФ₁ формируется корреляционная функция первого сигнала s₁, вида (4.4.22), тогда как второй сигнал s₂ на выход ОФ₁ практически не проходит. Аналогично на выходе ОФ₂ формируется реакция только на сигнал s₂. Напряжения U_Д1 и U_Д2 представляют собой огибающие напряжений u₁и u₂соответственно. На рисунке зачерненными кружочками отмечены моменты t₀ сравнения U_Д1 и U_Д2.

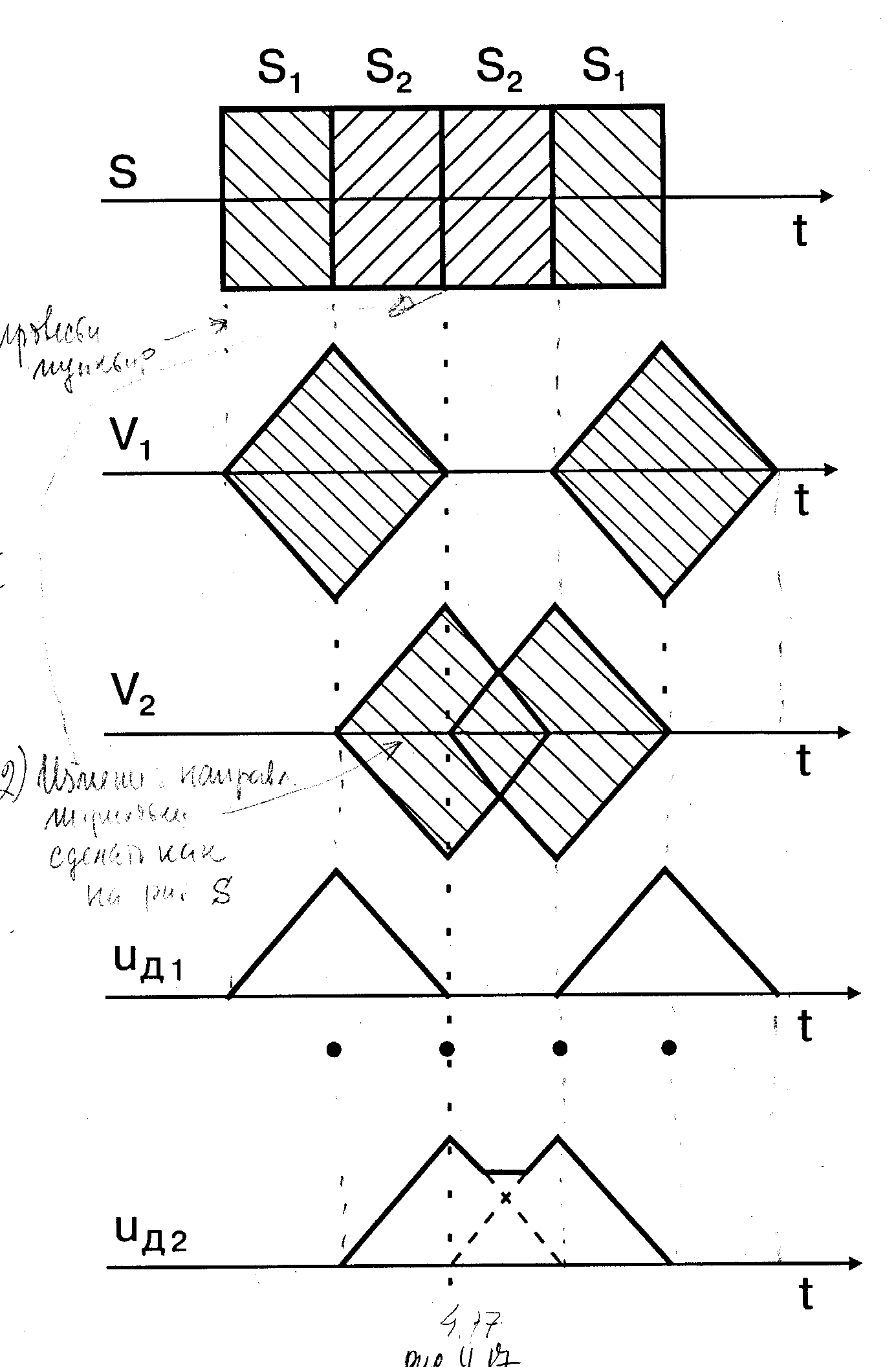
Рис. 4.17