Различение двух сигналов с неизвестной начальной фазой

4.6.1. Обсуждение задачи. Колебание u(t), поступающее на интервале наблюдения tÎ(0,T) на вход радиоприемного устройства

u(t)=s_i(t,j)+n(t), i=1 или 2 (4.6.1)

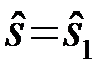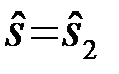представляет собой сумму сигнала s_i(t,j), который имеет вид одной из двух функций s₁или s₂, и основной гауссовской помехи n(t). Система по наблюдению {u(t),tÎ(0,T)} принимает решение о том, какой сигнал имеется на входе или . Заданными являются: статистика помехи n(t), детерминированные функции s₁(t,j) и s₂(t,j) времени и несущественного случайного параметра - начальной фазы j, априорные вероятности P₁ и P₂ посылки сигналов s₁ и s₂ (для сигналов КИМ P₁=P₂), распределение несущественного параметра j. Полагается, что начальная фаза распределена равновероятно в интервале jÎ(0,2p)

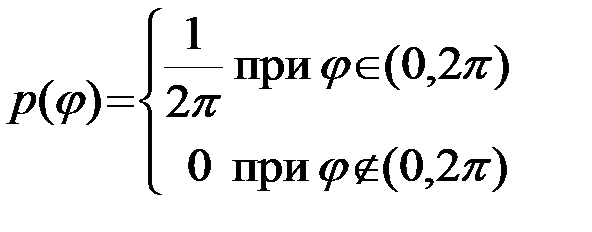(4.6.2)

Требуется определить оптимальный алгоритм обработки наблюдений и рассчитать качественный показатель оптимальной системы. Сформулированная задача отражает в частности, случай некогерентного *) приема сигналов КИМ, когда начальная фаза принимаемых сигналов неизвестна.

Согласно общему алгоритму оптимального различения двух сигналов (4.2.14) нужно по принятому колебанию {u(t),tÎ(0,T)} сформировать функции правдоподобия 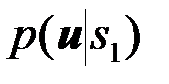и 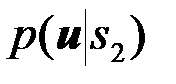первого s₁ и второго s₂ сигналов и при P₁=P₂ сравнить их между собой

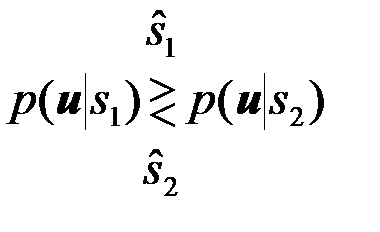. (4.6.3)

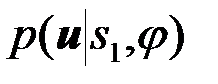Нам известно аналитическое выражение условной ПВ принимаемого колебания при условии, что сигнал полностью известен. При этом должны быть обусловлены вид функции s_i (например, s₁) и значение случайного параметра j. Иначе говоря, мы имеем аналитические выражения для функций и 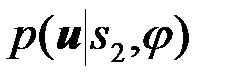, тогда как в решении (3) фигурируют функци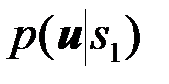и и 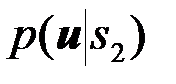- условные ПВ наблюдения u(t) при условии, что известен только вид функции s_i (s₁ или s₂), а начальная фаза 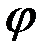может иметь произвольное значение.

4.6.2. Исключение случайной фазы из функции правдоподобия. На основании общего правила (3.7.7) исключение несущественных параметров из функции правдоподобия имеем

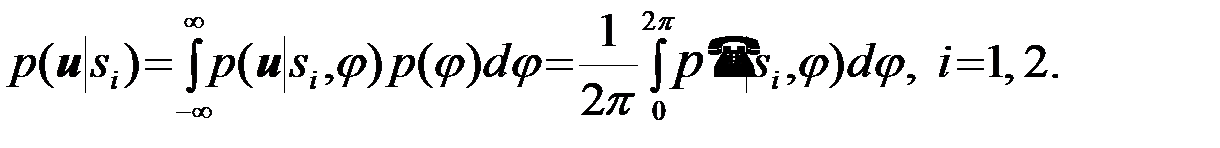(4.6.4)

Условная ПВ наблюдения при полностью обусловленном сигнале (s₁,j)

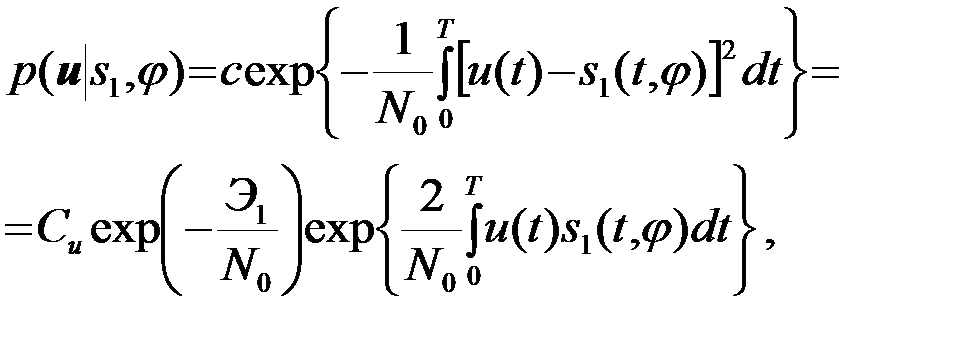(4.6.5)

где C_u - коэффициент, зависящий от но не от s₁(t,j)

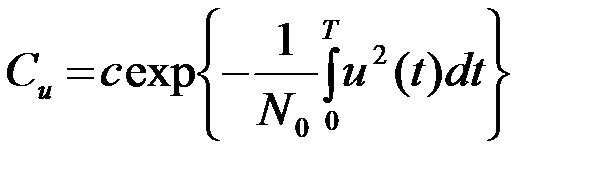, (4.6.6)

а Э₁ - энергия сигнала s₁ (от фазы j не зависит)

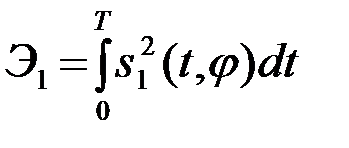. (4.6.7)

Преобразуем интеграл, входящий в (5),

.

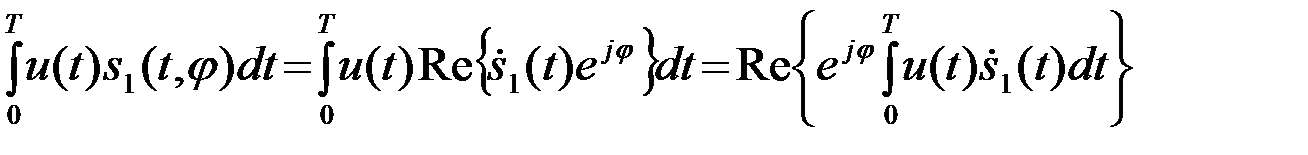Для этого введем определения: комплексного корреляционного интеграла

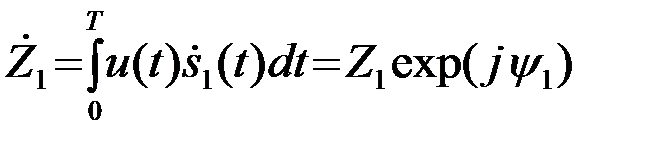(4.6.8)

принимаемого колебания u(t) с комплексным сигналом 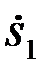(t), его модульного значения Z₁ и аргумента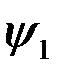

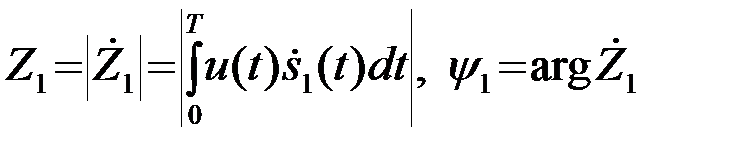. (4.6.9)

Тогда

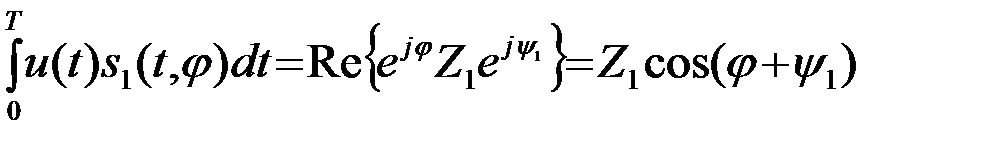(4.6.10)

и требуемая условная ПВ (4) после подстановки в нее (5) с учетом (10) принимает вид

.

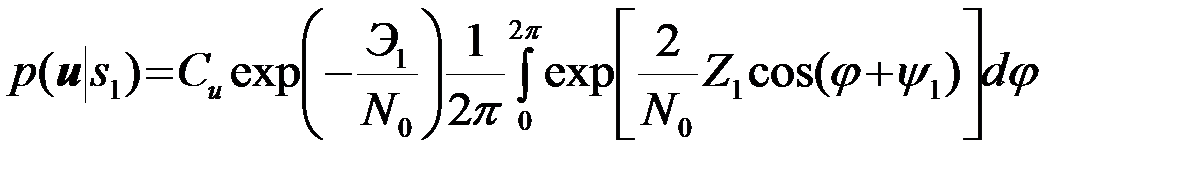Подынтегральная функция является 2p - периодической функцией переменной интегрирования j и смещение ее на y₁ не меняет величину интеграла по полному периоду 2p. Поэтому

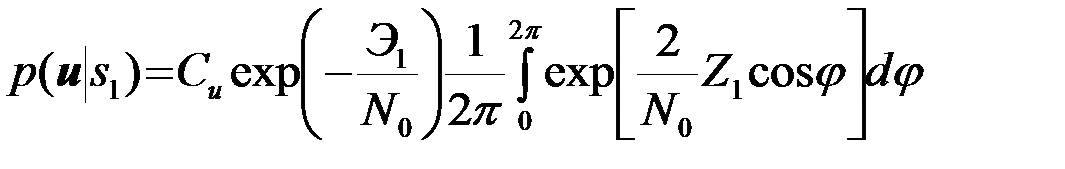. (4.6.11)

Функция

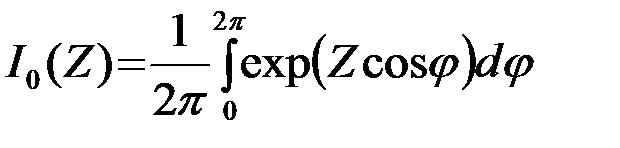(4.6.12)

называется модифицированной функцией Бесселя нулевого порядка. Она табулирована и широко используется. График монотонно возрастающей функции I₀(Z) приведен на рис.4.13а. Для малых и больших значений аргумента можно пользоваться приближенными формулами

пр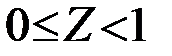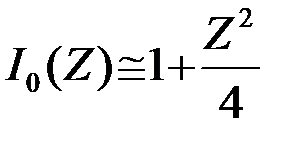и при 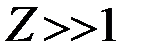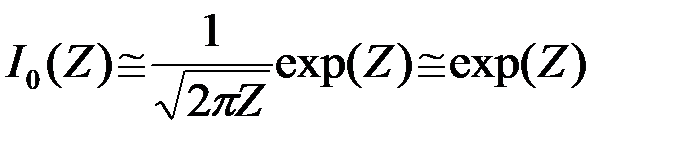. (4.6.13)

Окончательно получаем

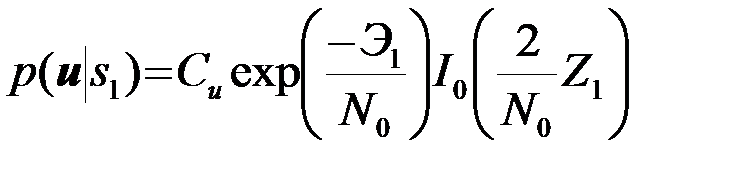. (4.6.14)

Аналогично

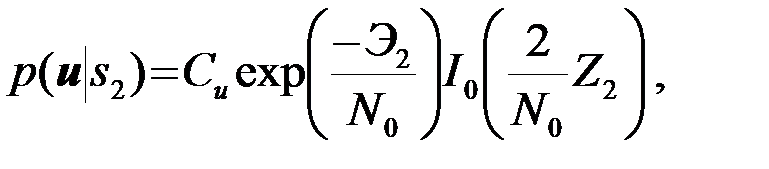(4.6.15)

где

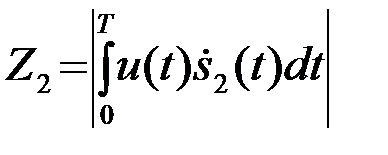(4.6.16)

модульное значение комплексного корреляционного интеграла наблюдения u(t) со вторым сигналом 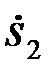(t).

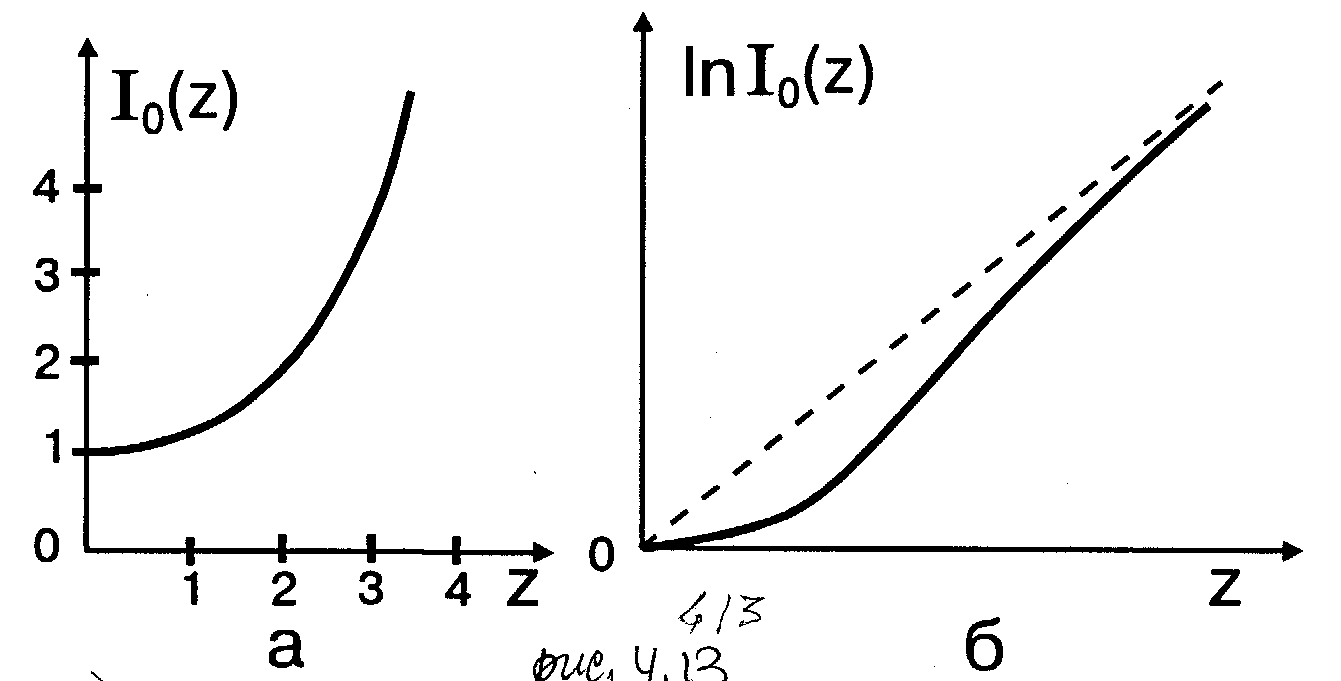
Рис. 4.13

Общий алгоритм оптимального различения двух сигналов (3) после логарифмирования правой и левой частей неравенства принимает вид

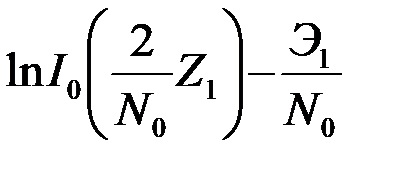
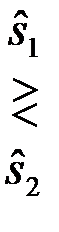
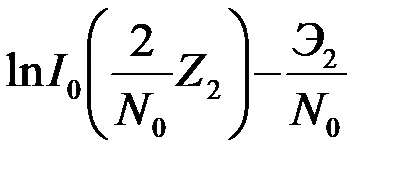. (4.6.17)

Функция lnI₀(Z₁) является монотонно возрастающей функцией своего аргумента, которая при малых и больших значениях Z согласно (13) приближенно равна (рис.13б)

пр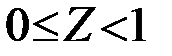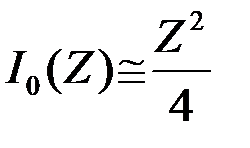и , при 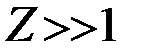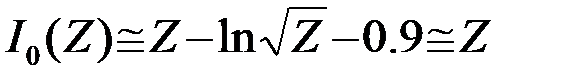(4.6.18)

Как и при простом различении, основной интерес представляют два случая.

4.6.3 Различение нулевого и ненулевого сигналов.В этом случае s₂=0, Э₂=0, Z₂=0; s₁=s, Э₁=Э, Z₁=Z и оптимальный алгоритм (17) преобразуется в

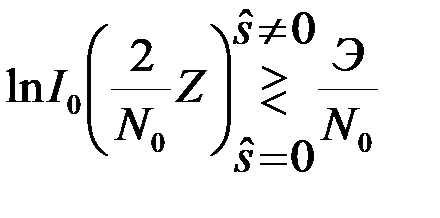. (4.6.19)

Введем определение для порогового уровня Z_п модульного значения комплексного корреляционного интеграла Z посредством формулы

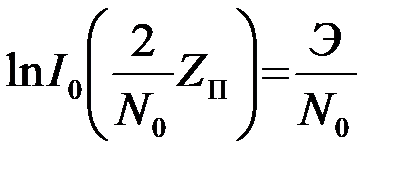. (4.6.20)

Так как в условиях нормального функционирования системы Э/N₀>>1, то (20) соответствует области, в которой согласно (18) функция lnI₀(×) приближенно равна своему аргументу. Поэтому

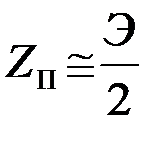. (4.6.21)

Окончательно оптимальный алгоритм (19) можно представить в виде

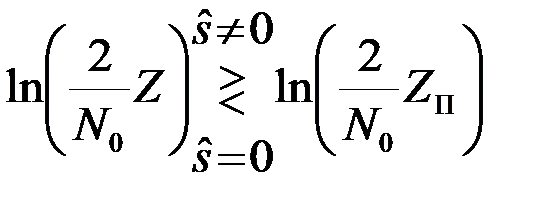или 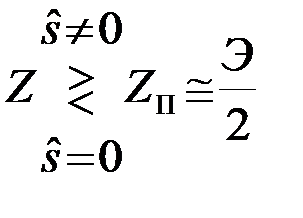. (4.6.22)

4.6.4. Различение сигналов с одинаковыми энергиями (Э1=Э2=Э).В этом случае одинаковые слагаемые Э/N0 в обеих частях неравенства (17) сокращаются. Кроме того, принимая во внимание, что монотонно возрастающая функция lnI₀(×) тем больше, чем больше ее аргумент, сравнение 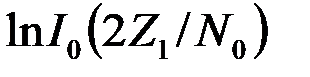и 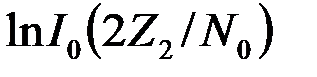можно заменить сравнением аргументов и оптимальному алгоритму различения придать вид

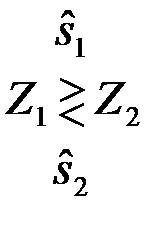. (4.6.23)

Оптимальная система по принятому наблюдению {u(t),tÎ(0,T)}, формирует два модульных значения комплексных корреляционных интегралов Z₁ и Z₂ и сравнивает их. Для общности в обе части неравенства (23) можно вписать один и тот же коэффициент K - масштабный множитель, характеризующий усиление.

Структурные схемы оптимального различения сигналов с неизвестной начальной фазой такие же, как и при различении полностью известных сигналов. Отличие состоит лишь в том, что вместо корреляционных интегралов должны формироваться модульные значения комплексных корреляционных интегралов наблюдения с образцом каждого из сигналов, который может поступить на вход системы. Соответственно основной существенной операцией при обработке наблюдений в процессе различения сигналов с неизвестной начальной фазой является формирование модульного значения комплексного корреляционного интеграла. Рассмотрим схемную реализацию этой операции.