Формуле (11) теперь можно придать следующий вид

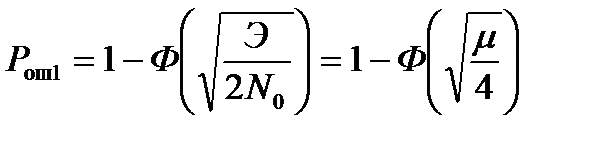, (4.5.14)

где m - отношение энергии сигнала Э к двусторонней спектральной плотности мощности помех на входе приемной системы N₀/2

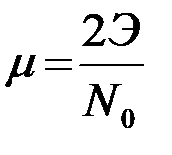. (4.5.15)

Параметр m является одним из основных параметров РТС и называется далее энергетическим отношением сигнал/помеха или энергетическим параметром. Отношение (4.4.20) пиковой мощности сигнала к мощности помех на выходе ОФ (P_c/P_п)_вых.оф равно этой же величине .

Расчет вероятности ошибки P_ош2 при передаче нулевого сигнала (a=0) совершенно аналогичен. Вероятность P_ош2 равна вероятности принятия решения 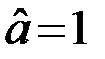(т.е. того, что Y>0,5Э) при условии, что передается сообщение a=0 (т.е. при условии, что u=n)

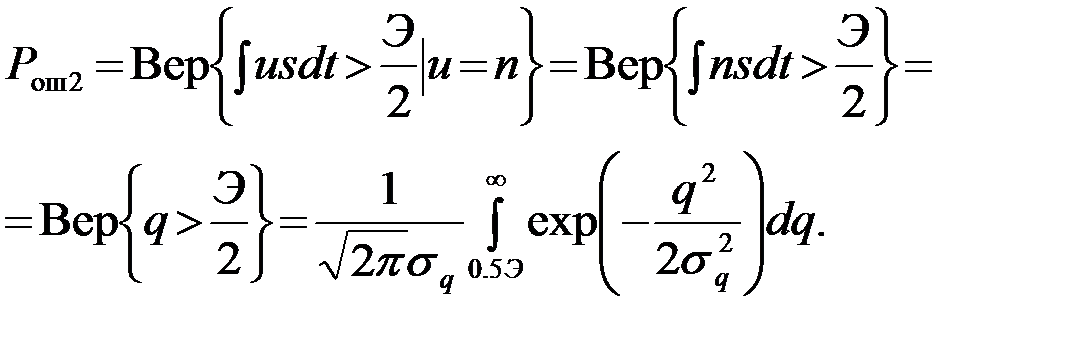
После подстановки (10), получаем

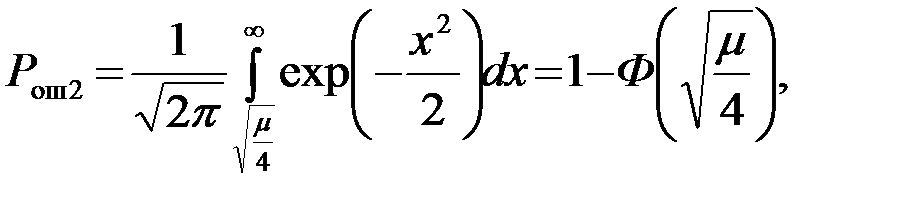(4.5.16)

что совпадает с (14). Вероятность ошибочных решений P_ош1 и P_ош2 получились равными друг другу и, следовательно, равными средней вероятности ошибочных решений P_ошср (3).

Окончательное выражение для качественного показателя системы

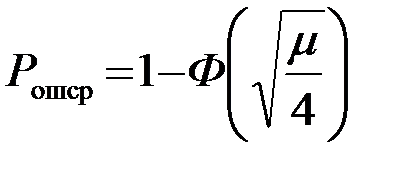. (4.5.17)

Заметим, что полученный результат можно обобщить:

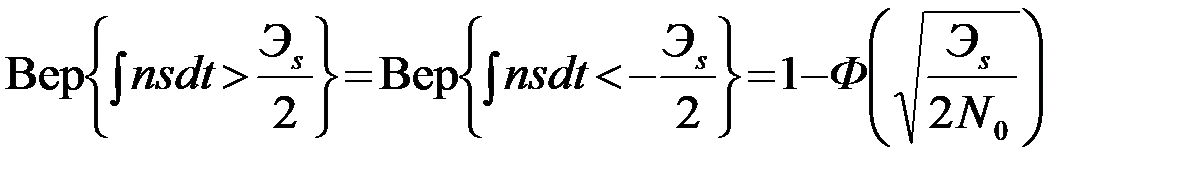(4.5.18)

где s(t) произвольная функция с энергией Э_s<¥, а n(t) - гауссовский белый шум со спектральной плотностью мощности N₀/2 (или гауссовский процесс с равномерным спектром N₀/2 в полосе ôfô 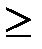F, включающей в себя спектр g_s(F)=F{s(t)}).

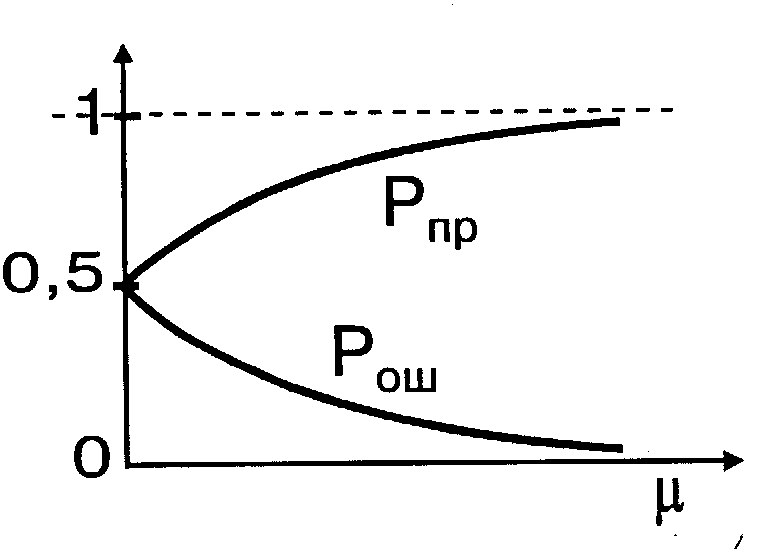
Рис. 4.12

Если сигнал очень слабый (если m®0), ситуация аналогична эксперименту с бросанием монеты ("герб" или "решка"). Фактически приходится отгадывать один из двух равновероятных исходов. В результате P_ошср®0,5 , что означает неразличимость сигнала. По мере увеличения сигнала P_ошср монотонно уменьшается. Закономерность, соответствующая формуле (17), иллюстрируется таблицей 4.1 и графиком (рис.4.12). В таблице и на графике, кроме вероятности ошибочных решений, представлена средняя вероятность правильных решений P_прср=1-P_ошср

Таблица 4.1

Pошср	0,5	10 -1	10 –2	10 -3	10 –4	10 –5
Pпрср	0,5	0,9	0,99	0,999	0,9999	0,99999
m		6,8		38,4	54,4	69,6

Различение двух сигналов с одинаковыми энергиями.

Полагаем

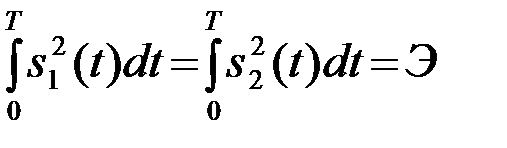(4.5.19)

и вводим определение для коэффициента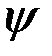

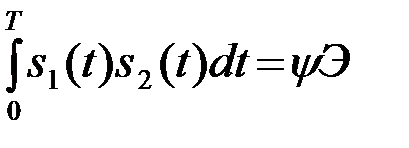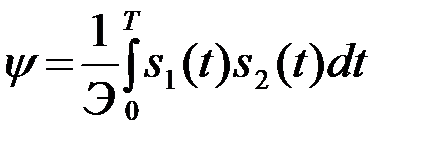, (4.5.20)

называемого коэффициентом корреляции сигналов s₁ и s₂ и характеризующего степень сходства этих сигналов. Коэффициент 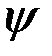может принимать значения в интервале (-1,1). Если 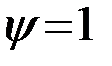, то сигналы совпадают 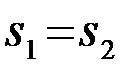, если 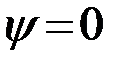, то сигналы не коррелированны (ортогональны). Наименьший коэффициент 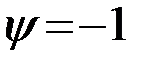получается при противоположных сигналах.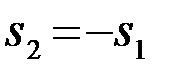

Руководствуясь оптимальным алгоритмом различения (4.3.7)

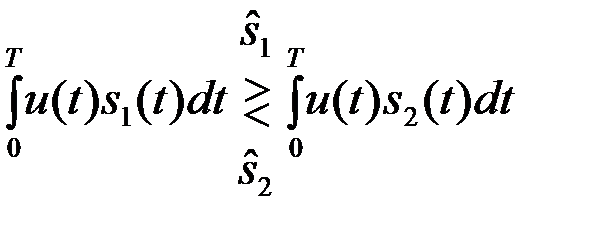(4.5.21)

находим условную вероятность ошибочного решения при условии, что передается s₁(u=s₁+n)

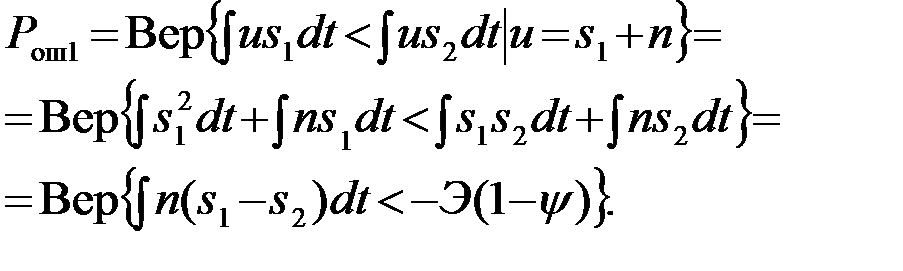
Введем обозначение 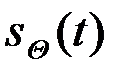для разностного сигнала

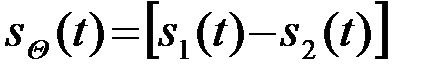(4.5.22)

с энергией

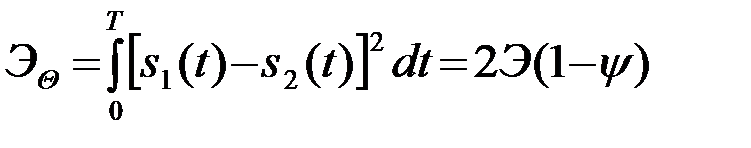. (4.5.23)

В результате получаем

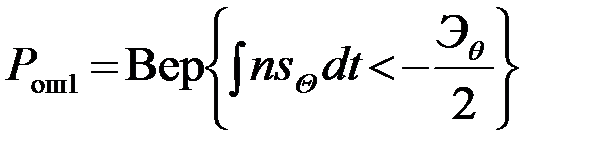. (4.5.24)

Расчетное выражение для P_ош1 приведено к виду (18). Поэтому

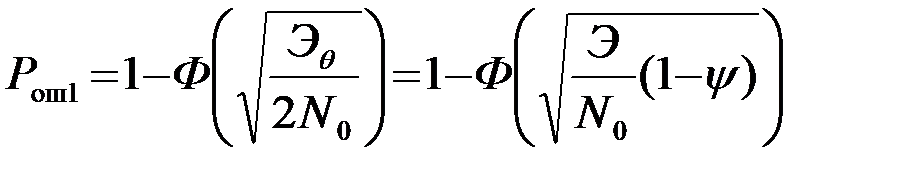. (4.5.25)

Вероятность ошибочных решений при передаче второго сигнала (u=s₂+n) равна

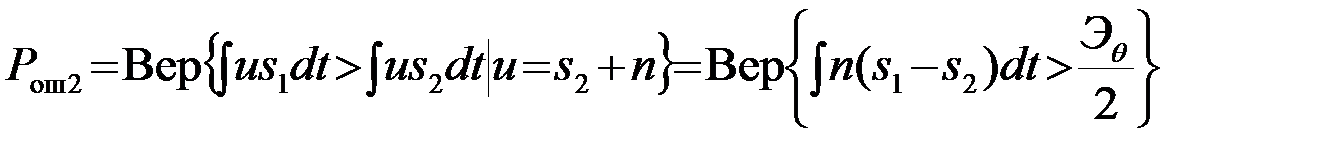(4.5.26)

что опять приводит к вероятности, определенной посредством (25).

Следовательно, при различении двух полностью известных сигналов с одинаковыми энергиями средняя вероятность ошибочных решений P_ошср=P_ош1=P_ош2

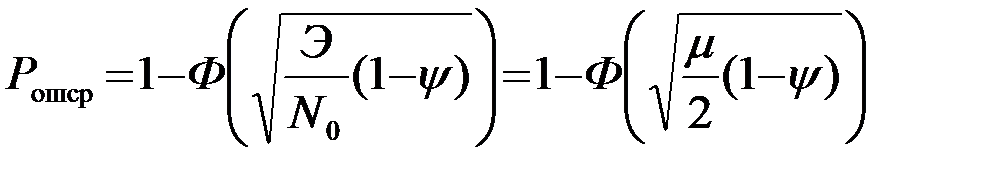. (4.5.27)

4.5.3. Общий случай различения двух полностью известных сигналов s1 и s2 с оптимальным алгоритмом решений (4.3.6)

.

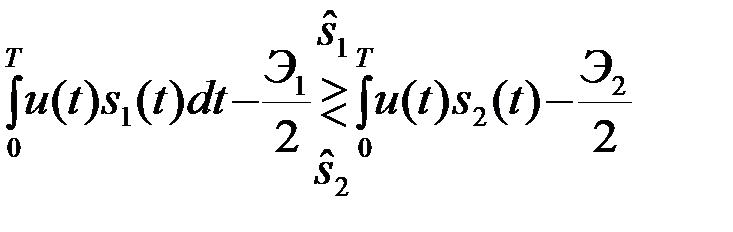Вероятность ошибочных решений P_ош1 при условии, что послан сигнал s₁(u=s₁+n)

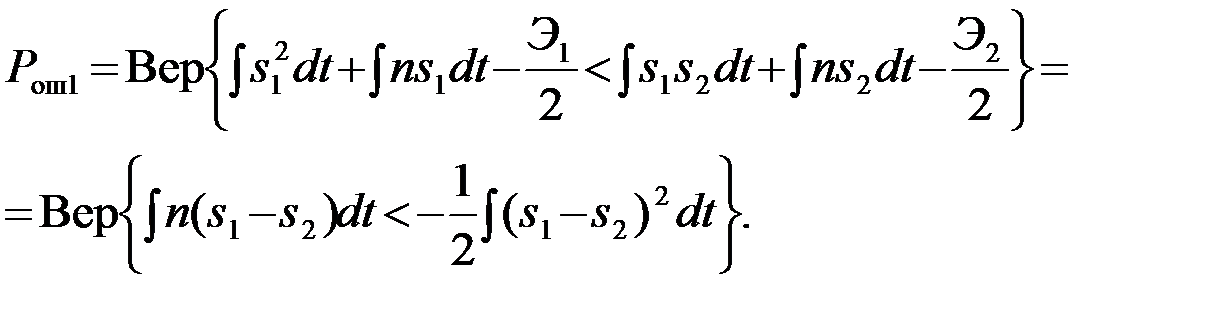(4.5.28)

опять выражается через разностный сигнал 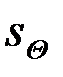и его энергию 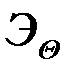и совпадает с (24). В результате в общем случае получаем выражение для средней вероятности ошибочных решений (P_ошср=P_ош1=P_ош2)

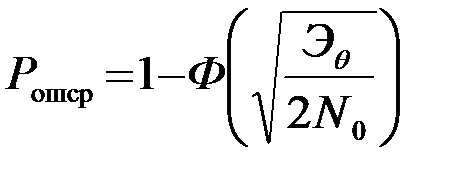(4.5.29)

которое включает в себя как частные случаи различение нулевого и ненулевого сигналов ( 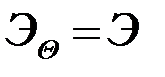) и различение сигналов с одинаковыми энергиями ( ).

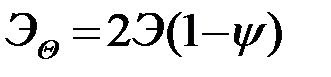Расчетные соотношения, полученные на упрощенной модели различения полностью известных сигналов, позволяют сделать ряд практических выводов, имеющих в значительной мере общий характер.