Помеховая составляющая выхода ОФ

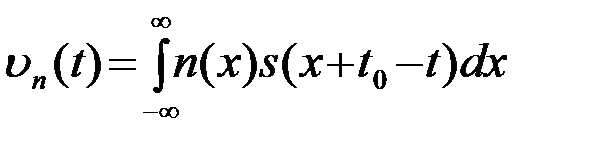, (4.4.16)

при основной гауссовской помехе n(t), является гауссовским центрированным, стационарным СП, который полностью определяется своей корреляционной функцией

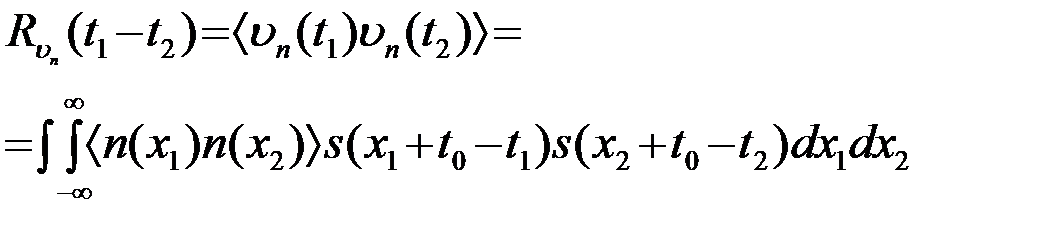. (4.4.17)

Интеграл произведения функций во временной области (16), равный интегралу произведения соответствующих спектров в частотной области, не зависит от верхней частоты F спектра помехи n(t), если спектр сигнала не имеет частотных составляющих вне полосы ôfô³F, занятой помехой. Поэтому для упрощения вычислений интегралов типа (16) и (17) здесь и в дальнейшем для помехи n(t) с равномерным возможно ограниченным спектром мощности будет использоваться модель белого шума (F®¥). 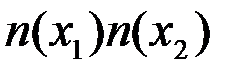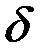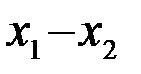При этом =(N₀/2) ( ) и

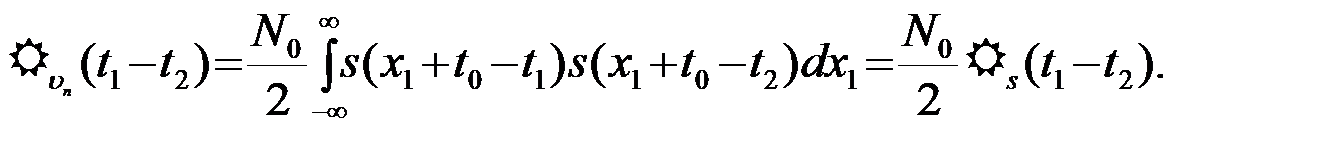(4.4.18)

Корреляционная функция помеховой составляющей 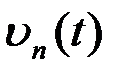с точностью до коэффициента 0,5N₀ совпадает с корреляционной функцией сигнала (с сигнальной составляющей 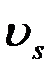). Дисперсия (средняя мощность) помех на выходе ОФ

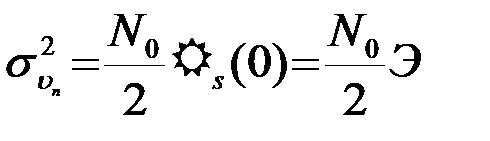. (4.4.19)

Соответственно максимальное отношение сигнал/помеха по мощности (P_с/P_п)_вых.оф, получающееся на выходе ОФ в момент формирования корреляционного интеграла 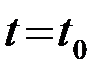, равно

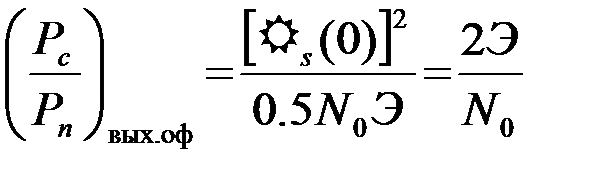. (4.4.20)

Пример 4.4.2. Приведем конкретный пример сигнальной составляющей выхода ОФ, характерный для сигналов КИМ, имеющих вид П - образного радиоимпульса (рис.4.9а)

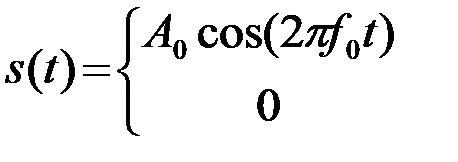
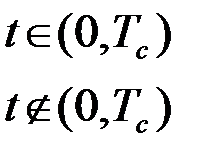. (4.4.21)

Корреляционная функция сигнала (21), принимая во внимание, что произведение s(t)s(t-t) отличается от нуля на интервале tÎ(t,T_с) при 0£t£T_с

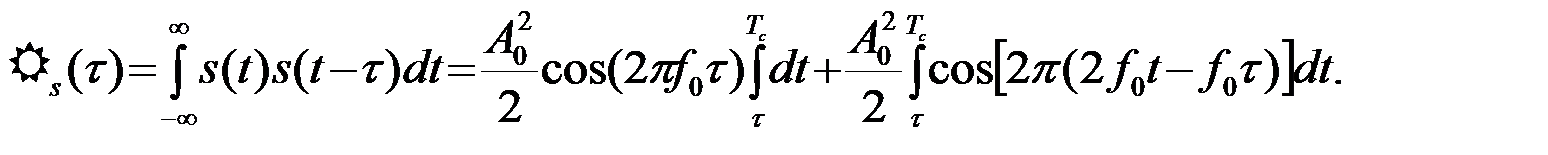
Второй интеграл в последнем выражении практически равен нулю, так как площади под положительными и отрицательными полуволнами быстро осциллирующей косинусоиды взаимно компенсируются. Учитывая четность корреляционной функции, получаем

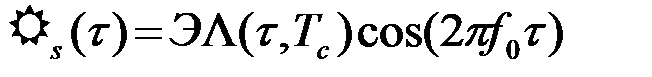, (4.4.22)

где (t,T_c) - "треугольная" функция

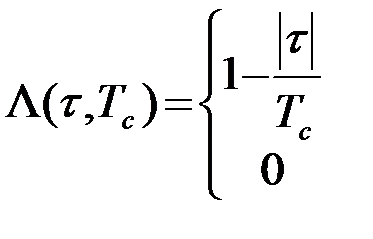
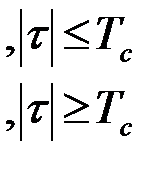. (4.4.23)

Сигнальная составляющая ОФ (t₀=T_с)

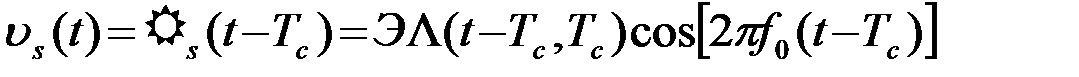4.4.24)

изображена на рис. 4.9б.

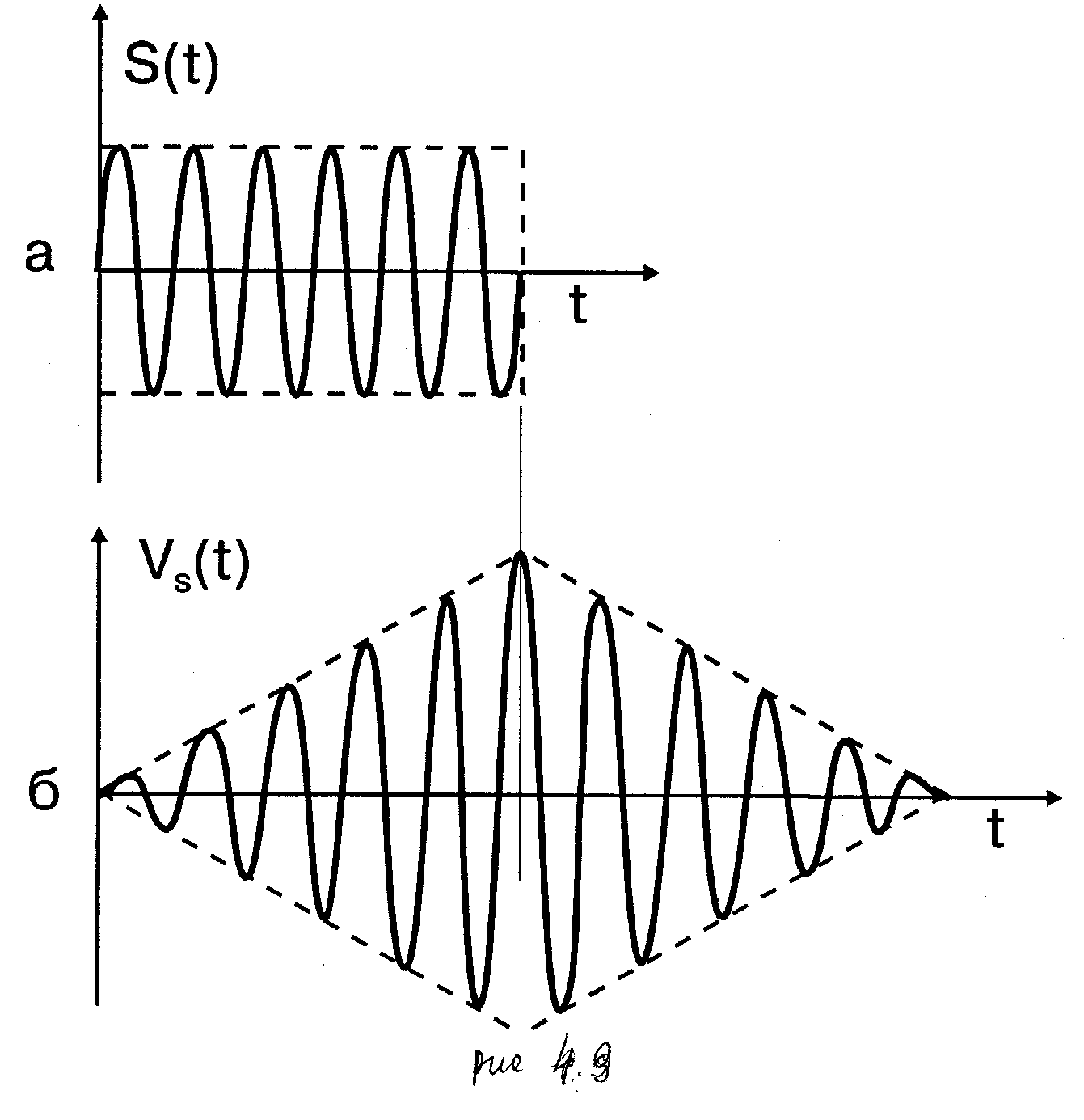
Рис. 4.9

Сформулируем основной результат. Импульсная характеристика ОФ представляет собой зеркальное отображение 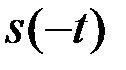ожидаемого сигнала s(t), смещенное по времени на величину t₀, равную моменту времени окончания t_к сигнала (t₀=t_к). При этом импульсная характеристика h₀(t) начинается в момент времени t=0, а выход ОФ совпадает с корреляционным интегралом в момент t₀=t_к. ОФ инвариантен относительно временного положения сигнала. При любом временном положении t сигнала 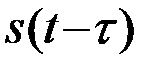корреляционный интеграл Y=υ(t₀) - формируется в момент t_к(t₀=t_к) окончания сигнала 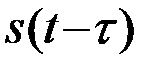. Отметим также, что оптимальный согласованный фильтр 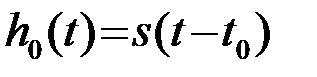обеспечивает максимально возможное отношение сигнал/помеха на выходе фильтра. Действительно, запишем отношение 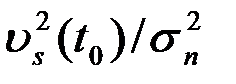на выходе произвольного фильтра с ИХ h(t)

.

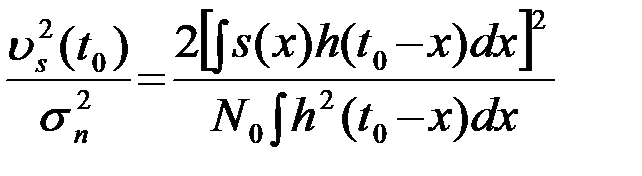Домножим числитель и знаменатель последнего выражения на 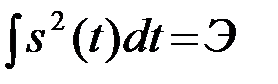. В результате получим

.

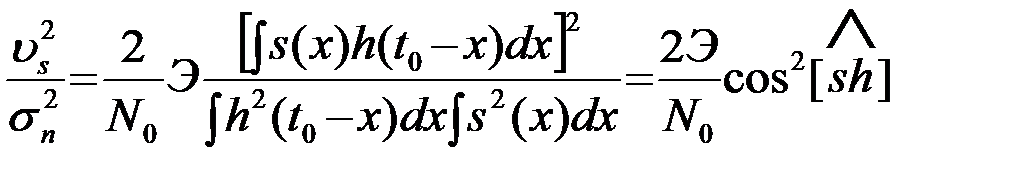Косинус угла в функциональном пространстве достигает максимума, равного 1, при h(t₀-x)=s(x) или h(t)=s(t₀-t) т.е. когда фильтр согласован с сигналом. При этом совпадает с (20).

4.4.4. Частотная характеристика OФ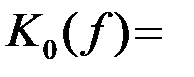

.

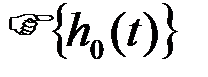
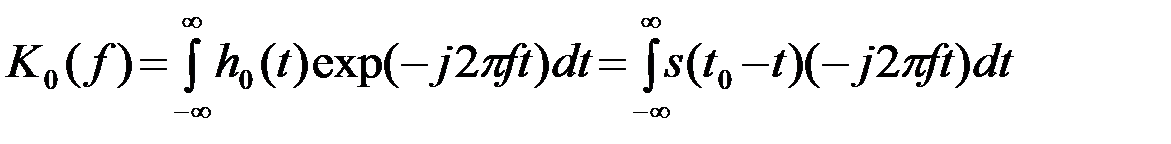После подстановки t₁=(t₀-t), (t=t₀-t₁) получаем

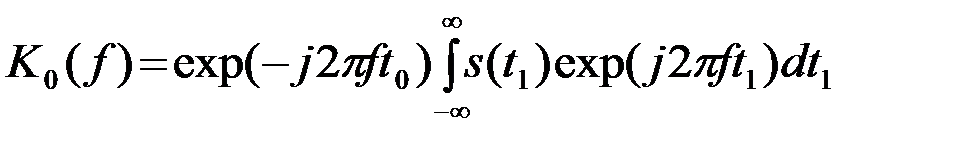
или

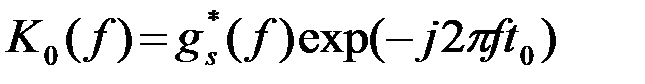
(4.4.25)

где 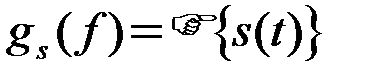- спектр сигнала s(t).

Частотная характеристика ОФ с точностью до несущественного множителя exp(-j2pft₀), характеризующего временное смещение на t₀, представляет собой функцию, комплексно сопряженную по отношению к спектру сигнала g_s(f). Соответственно амплитудно-частотная характеристика ОФ

|K₀(f)| =|g_s(f)| (4.4.26)

совпадает с амплитудным спектром сигнала, а фазочастотная характеристика ОФ

argK₀(f)=-arg g_s(f)-2pft₀ (4.4.27)

отличается только знаком от фазового спектра сигнала (с точностью до несущественного слагаемого 2pft₀, обусловленного смещением по времени 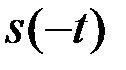на t₀).

Корреляционный интеграл может быть представлен в спектральной области [g_u(f)=F{u(t)}]

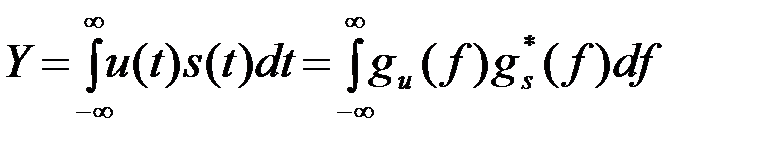(4.4.28)

или

.

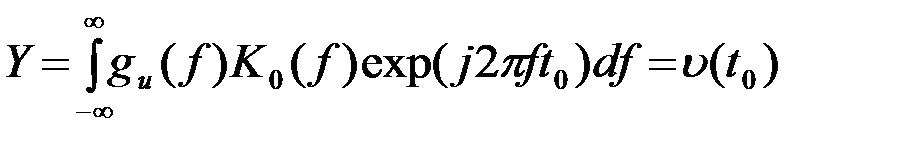4.4.5. В заключение приведем структурную схему приема сигналов КИМ ЧМ, построенную по методу оптимальной фильтрации (рис.4.10). Схема предназначена для различения последовательности сигналов, каждый из которых может принимать вид s₁(t) или s₂(t), и имеет два канала обработки с фильтрами ОФ₁ и ОФ₂. Импульсные характеристики этих фильтров h₀₁(t)=s₁(t₀-t) и

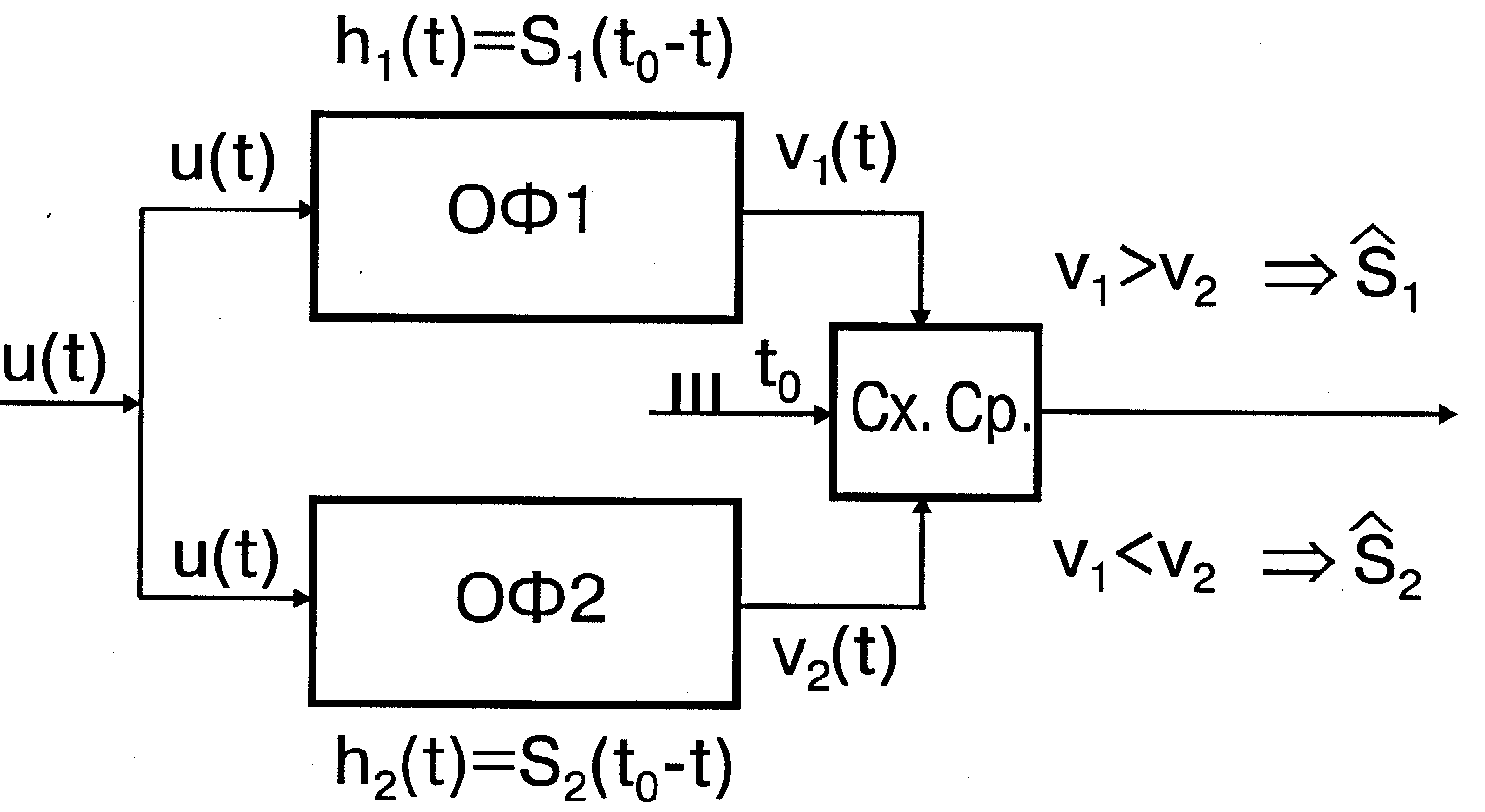
Рис. 4.10

h₀₂(t)=s₂(t₀-t) согласованы с сигналами s₁ и s₂ соответственно. Особенность состоит в том, что на схему сравнения (Сх.Ср.) поступают из системы синхронизации тактовые импульсы, фиксирующие моменты t_к окончания двоичных сигналов, в которые должно производиться сравнение выходов υ₁(t) и υ₂(t).