Схемные методы формирования корреляционного интеграла

В практических схемах используется два метода формирования корреляционного интеграла

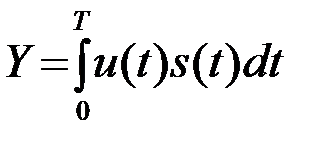(4.4.1)

принимаемого колебания u(t) с образцом сигнала s(t), который может поступить на вход приемной системы, - это метод корреляции и метод оптимальной фильтрации. Здесь и далее T - интервал, длительностью T, вне которого s(t)=0, например, tÎ(0,T),tÎ(-0,5T;0,5T) и т.д.

4.4.1.Метод корреляции(рис.4.4) сводится к прямому схемному моделированию корреляционного интеграла (1). В схему входит опорный генератор (ОГ), который вырабатывает колебание s(t), совпадающее по форме с сигналом, фигурирующим в корреляционном интеграле (1), перемножитель ( ), производящий операцию умножения принимаемого колебания u(t) на опорный сигнал s(t), и интегратор, осуществляющий интегрирование подводимых к нему колебаний u(t)s(t). В результате на выходе схемы формируется корреляционный интеграл (1). Схема очень проста в идейном отношении. Некоторые практические трудности представляет необходимость формировать в ОГ колебание, совпадающее (с точностью до произвольного коэффициента K) по форме и по временному положению с ожидаемым на входе сигналом s(t).

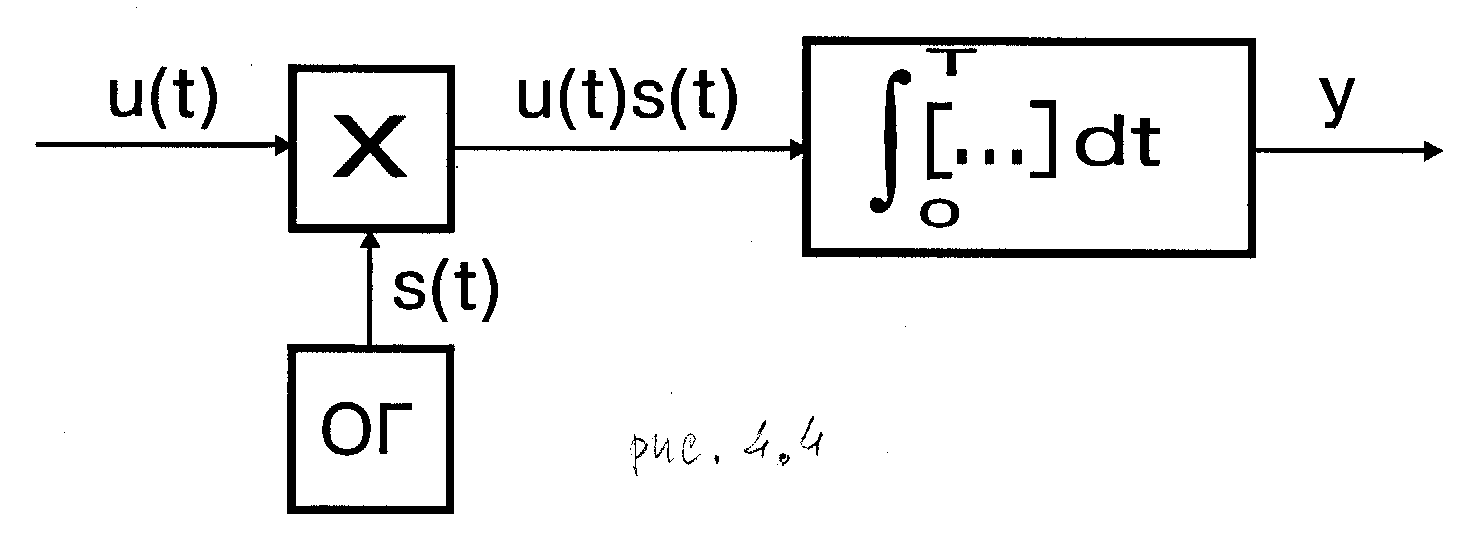
Рис. 4.4

4.4.2.Метод оптимальной фильтрации основан на формировании корреляционного интеграла при помощи оптимального фильтра (ОФ), представляющего собой ЛИВ-систему (рис.4.5) с соответствующим образом подобранной импульсной характеристикой h₀(t). Поясним выбор импульсной характеристики h₀(t) оптимального фильтра. При подаче на вход произвольной ЛИВ-системы с импульсной характеристикой h(t) колебания u(t) выходной эффект (выход) системы 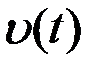имеет вид

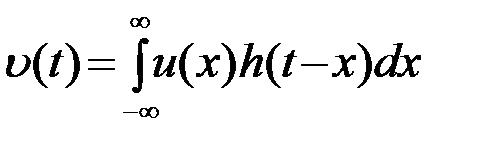. (4.4.2)

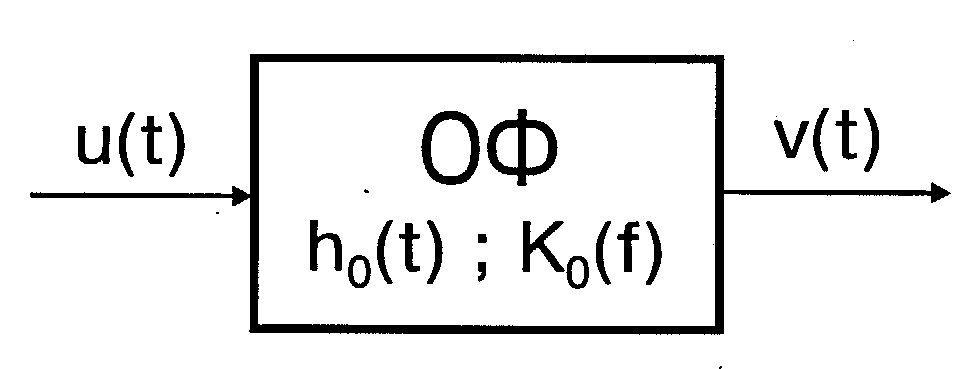
Рис. 4.5

Мы стремимся к тому, чтобы выход 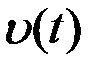совпал с корреляционным интегралом Y. Так как корреляционный интеграл (1)-число, а выход (2)-функция времени, то совпадение возможно только в некоторый фиксированный момент времени 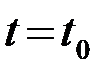. Уравнение, определяющее импульсную характеристику ОФ 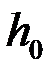(t), можно записать так

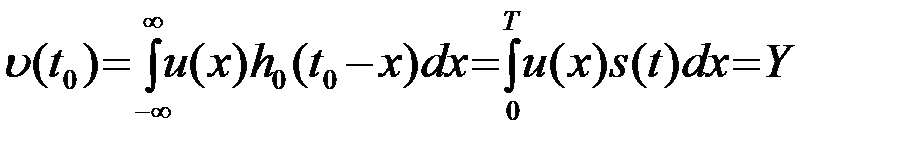, (4.4.3)

откуда следует, что 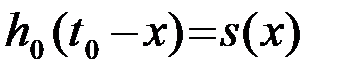, или, обозначая 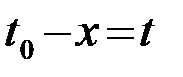, окончательно получаем

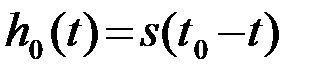. (4.4.4)

Различие в пределах интегрирования в первом и во втором интегралах (3) значения не имеет: функция 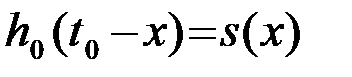вне интервала наблюдения T тождественно равна нулю. Следовательно, импульсная характеристика ОФ согласуется с видом сигнала s(t), для которого формируется корреляционный интеграл. Поэтому ОФ называется также согласованным фильтром (СФ). В выражении (4) для 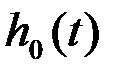может быть введен произвольный коэффициент K, характеризующий усиление. В теоретических рассмотрениях обычно принимают K=1.

Обсудим несколько подробнее результат (4). В частности, уточним значение 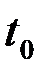. Положим сигнал s(t), входящий в корреляционный интеграл (1), имеет вид, изображенный на рис.4.6.

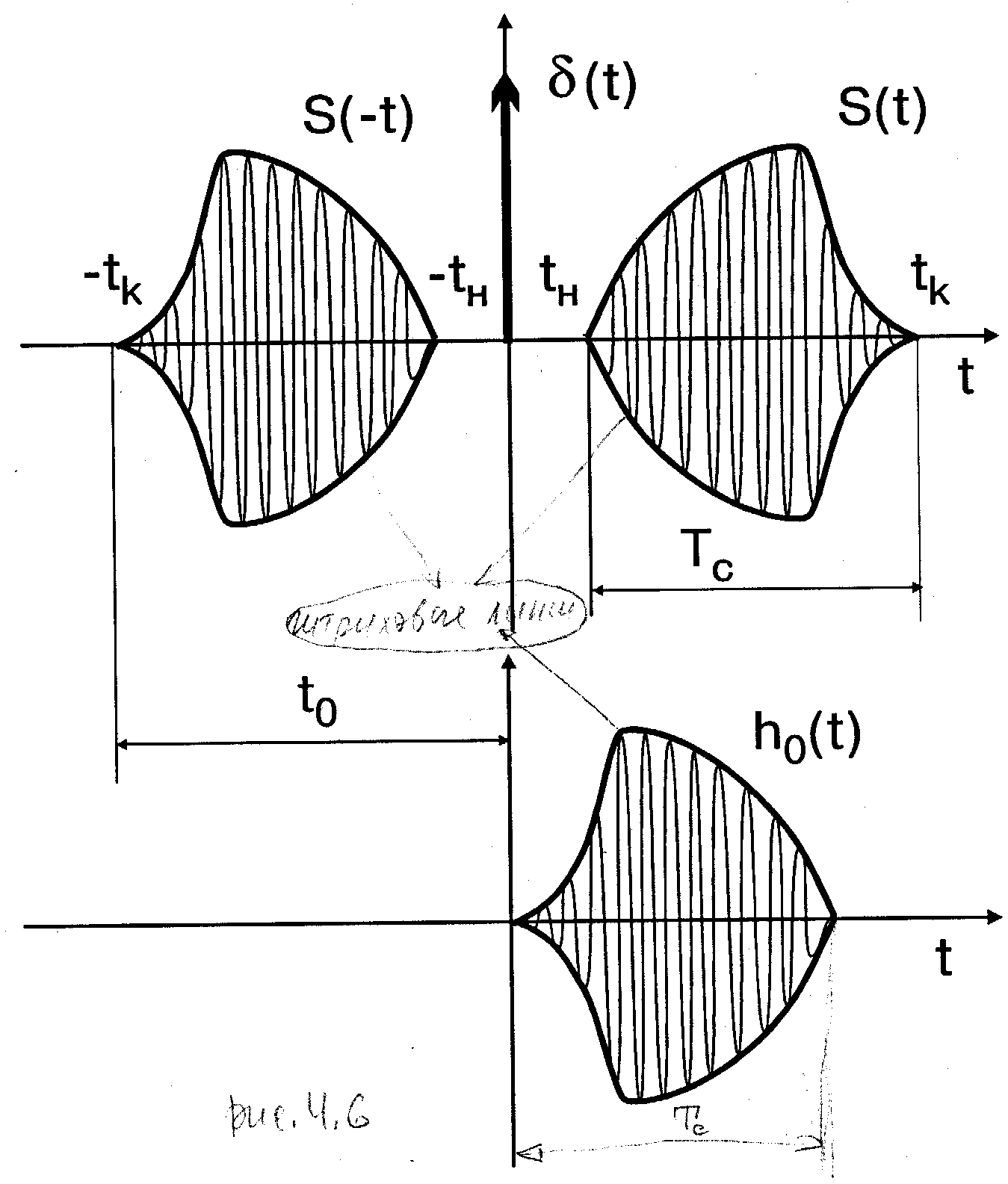
Рис. 4.6

На рисунке отмечены моменты t_н и t_к начала и окончания сигнала. Длительность сигнала не превосходит интервал наблюдения T_с=t_к-t_н£T. На рис.4.6 изображена также функция s(-t), являющаяся зеркальным отображением сигнала s(t). Функция s(-t) с математической точки зрения можно было бы принять в качестве импульсной характеристики ОФ h₀(t). В этом случае t₀=0 и υ(0)=Y. Однако импульсная характеристика h₀(t)=s(-t) (рис.4.6) физически нереализуема. Импульсная характеристика-реакция на воздействие в виде d -функции, поданной в момент 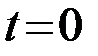, не может появиться раньше воздействия. Поэтому условие h(t)=0 при является условием физической реализуемости фильтра. Исходя из этого условия характеристику s(-t) следует сместить на некоторую величину t₀, так чтобы импульсная характеристика s(-t+t₀) целиком располагалась на положительной полуоси tÎ(0,¥) (рис.4.6). Из рисунка следует, что t₀ должно быть: t₀³t_к. В дальнейшем принимается минимальное значение

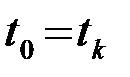. (4.4.5)

Это значит, что импульсная характеристика начинается в 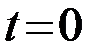, а корреляционный интеграл формируется на выходе ОФ в момент окончания сигнала s(t): υ(t_к)=Y. В частном случае, когда сигнал, длительности T_с, начинается в момент t=0(t_н=0),t_к=T_с и υ(T_с)=Y. Приведем пример определения импульсной характеристики ОФ.

Пример 4.4.1. В качестве сигнала выберем широко используемый в радиолокации линейно модулированный по частоте (ЛЧМ) радиоимпульс

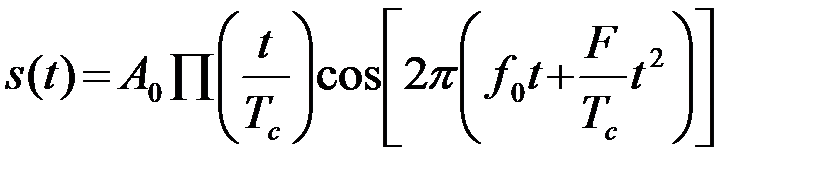(4.4.6)

и определим импульсную характеристику h₀(t)=s(t₀-t) согласованную с этим сигналом. На рис.4.7 показано изменение во времени огибающей A(t) и мгновенной частоты f(t) ЛЧМ радиоимпульса (6)

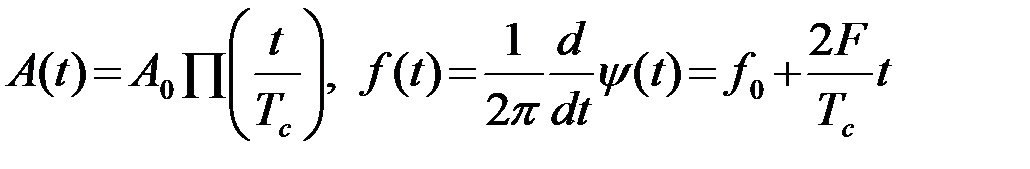, (4.4.7)

где y(t)=2p(f₀t+Ft²/T_c) - полная фаза колебаний радиоимпульса. На рис.4.8 изображены ЛЧМ радиоимпульс s(t), его зеркальное отображение s(-t) и импульсная характеристика ОФ (t₀=t_к=0,5T_с)

h₀(t)=s(0,5T_с-t). (4.4.8)

Таким образом, импульсная характеристика ОФ представляет собой зеркальное отображение сигнала s(-t), сдвинутое на положительную полуось времени tÎ(0,¥).

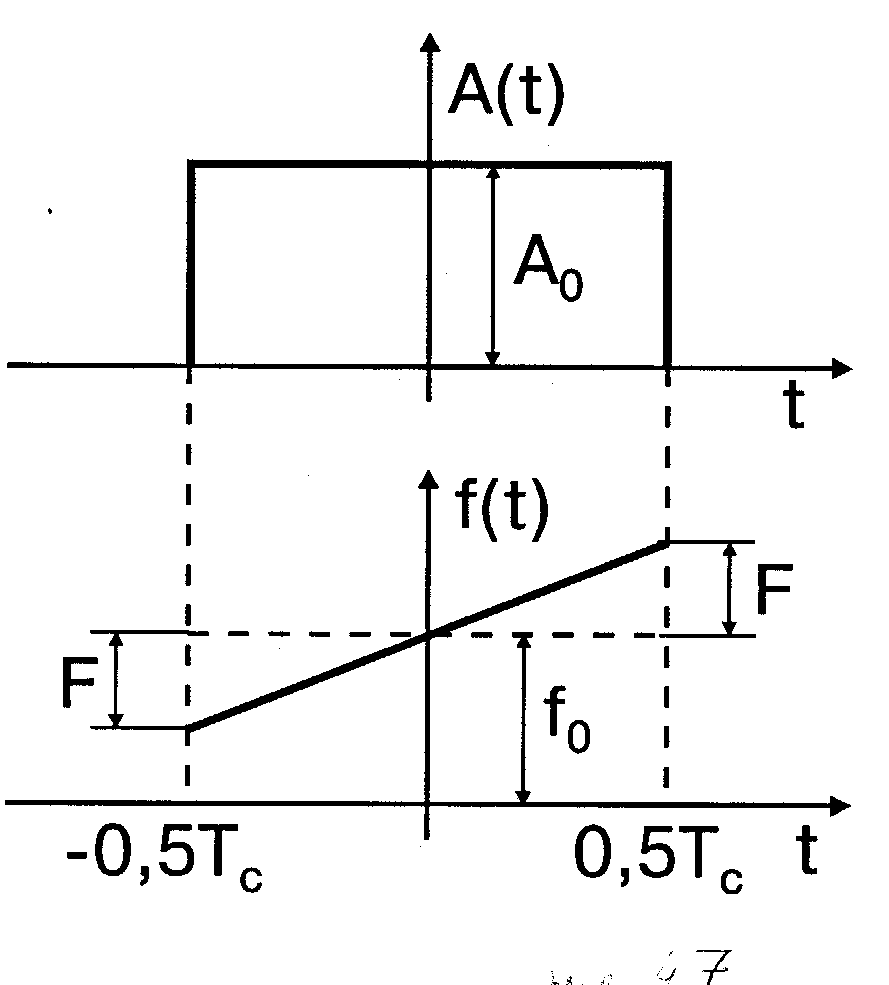
Рис. 4.7

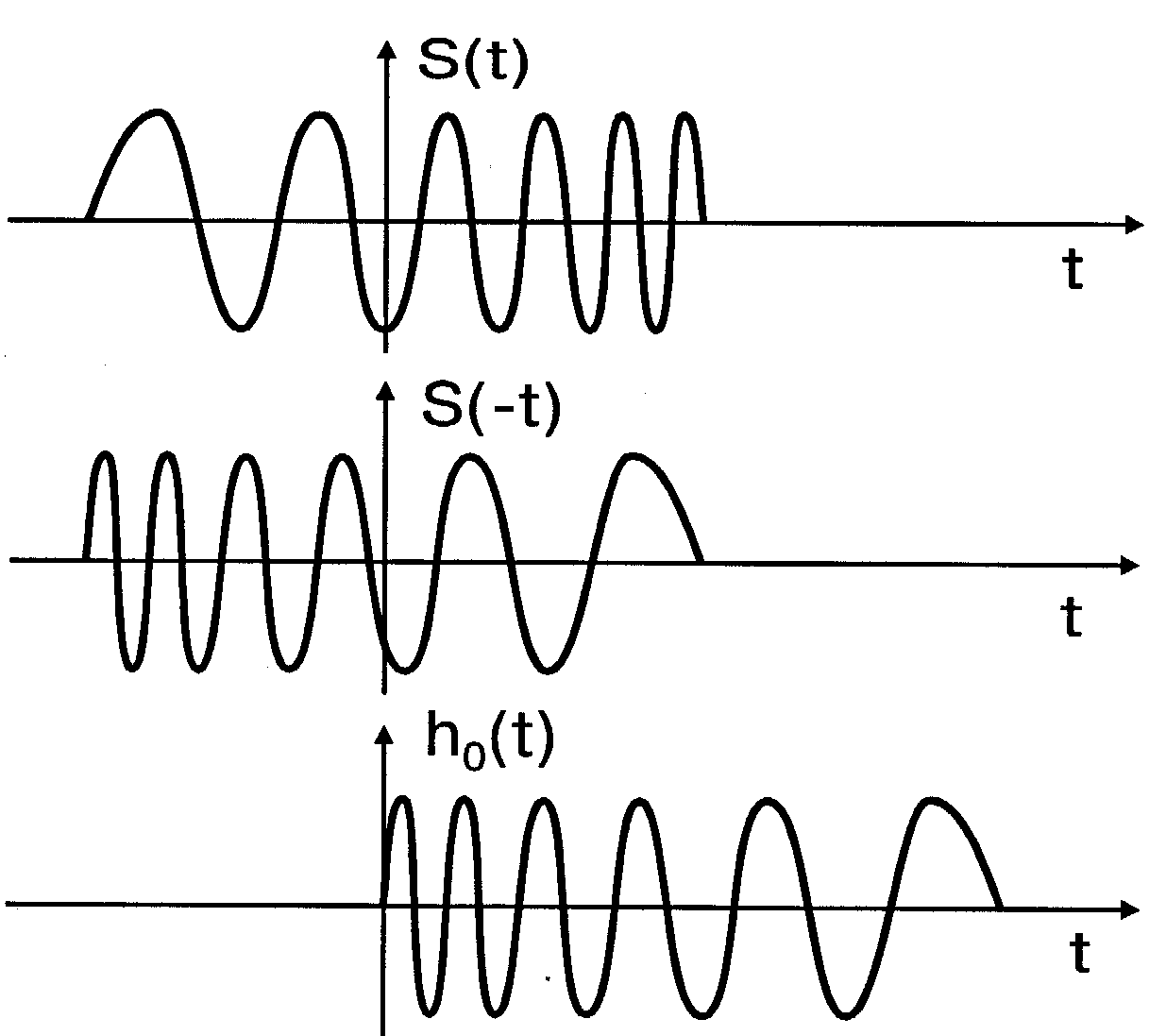
Рис. 4.8

Заметим, что для сигналов s(t), симметричных относительно некоторой оси 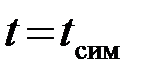, зеркальный сигнал s(-t) совпадает по форме с исходным s(t). При этом 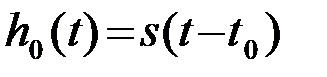, где 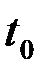опять выбирается из условия h₀(t)=0при 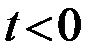. В частности, при 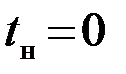можно принять 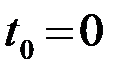и .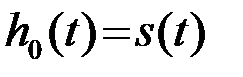

4.4.3. Прохождение сигнала и помехи через ОФ.Выход ОФ

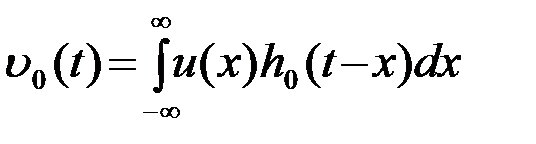. (4.4.9)

Так как согласно (4)

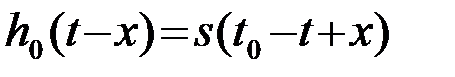, (4.4.10)

то (9) принимает вид

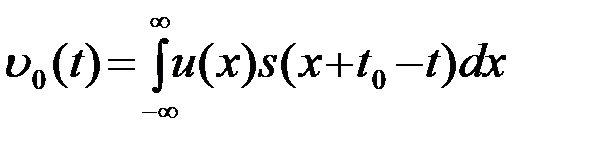. (4.4.11)

Принимаемое колебание является суммой сигнала и помехи u=s+n. Поэтому и выход (11) представляет собой сумму сигнальной 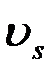и помеховой 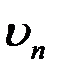составляющих

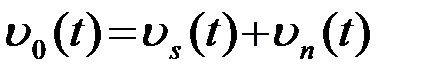. (4.4.12)

Рассмотрим эти составляющие

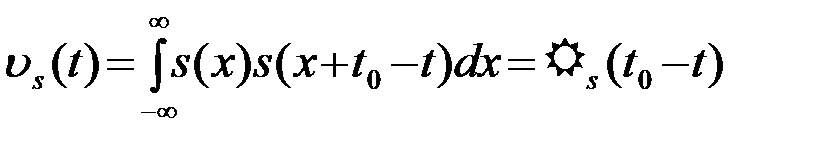, (4.4.13)

где 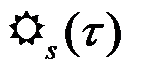- (временная) корреляционная функция ожидаемого сигнала s(t)

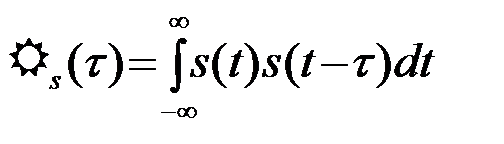, (4.4.14)

являющаяся четной функцией с максимумом, равным энергии сигнала Э, в нуле

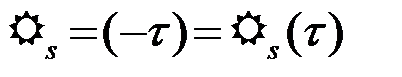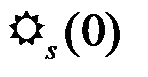, =Э=max. (4.4.15)

Следовательно, сигнальная составляющая выхода ОФ воспроизводит корреляционную функцию сигнала 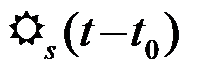и имеет максимум, равный Э, в момент 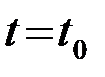формирования корреляционного интеграла Y.