Различение двух полностью известных сигналов

Простейшей задачей различения является задача различения двух полностью известных сигналов. В этом случае полагается, что принимаемые полезные сигналы не содержат случайных несущественных параметров (или значение этих параметров точно известно заранее). Задача моделирует в первую очередь так называемый когерентный прием, при котором начальная фаза принимаемого сигнала известна на приемной стороне. Такой прием возможен, например, в условиях, когда фаза медленно изменяются во времени. Это позволяет отслеживать (измерять) ее на приемной стороне и тем самым обеспечивать ее знание к моменту приема очередного двоичного сигнала. Кроме того, задача представляет первое, идеализированное рассмотрение более широкого класса задач различения и ее решение позволяет сделать ряд важных практических выводов общего характера. Формулировка задачи аналогична приведенной в предыдущем параграфе.

На вход системы на заданном интервале наблюдения tÎ(0,T) поступает колебание

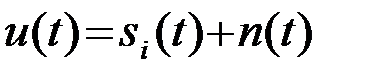, i =1 или 2, (4.3.1)

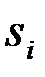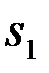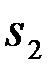состоящее из полезного сигнала , который может принимать одно из двух значений или , и стандартной гауссовской помехи n(t). Система по наблюдению {u(t),tÎ(0,T)} принимает решение о том, какой сигнал присутствует на входе 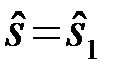или .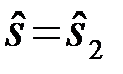

Заданы: детерминированные функци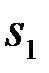и (t) и 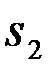(t), априорные вероятности P₁ и P₂ первого и второго сигналов, статистика помехи.

Требуется определить оптимальный алгоритм преобразования наблюдения {u(t),tÎ(0,T)}, которое тождественно определяется вектором наблюдений 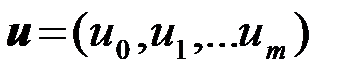, в решение 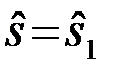или .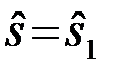

Априорные сведения, приведенные в формулировке задачи, позволяют записать аналитические выражения для условных (по 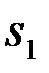и 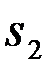) ПВ наблюдения - функций правдоподобия 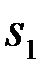и 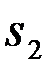(см.§3.7)

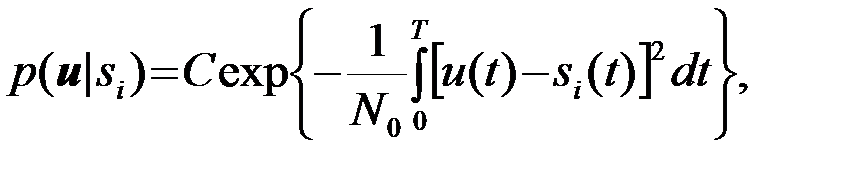i=1,2 . (4.3.2)

Согласно общему оптимальному правилу решений (4.2.14) нужно сформировать два числа 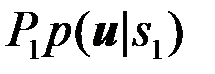и 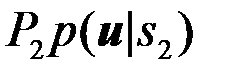и сравнить их

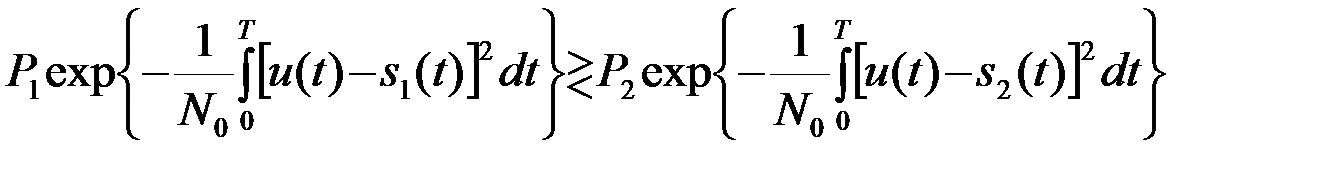, (4.3.3)

т.е. выяснить, какое из 2-х неравенств > или < имеет место. Неравенство не нарушается, если обе его части подвергнуть произвольному монотонно возрастающему преобразованию. Поэтому после логарифмирования (3), возведения в квадрат двучленов и интегрирования получаем оптимальный алгоритм различения полностью известных сигналов

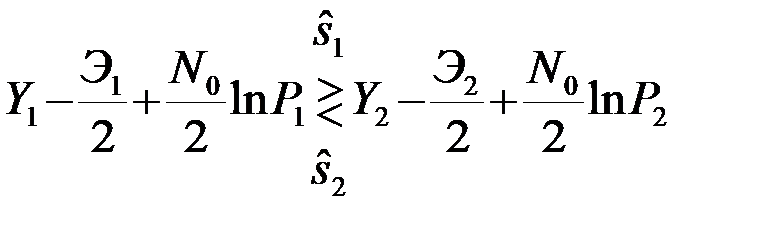, (4.3.4)

где Y₁ и Y₂ - так называемые корреляционные интегралы принимаемого колебания u(t) с первым 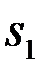(t) и вторым 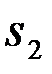(t) сигналом

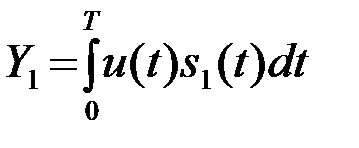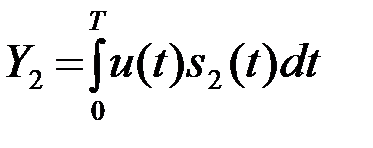, , (4.3.5)

а Э₁ и Э₂ - энергия первого и второго сигналов.

Применительно к системам КИМ двоичные сообщения 0 и 1 ( 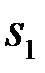и 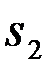) можно считать равновероятными P₁=P₂=0,5. При этом оптимальный алгоритм различения (4) упрощается

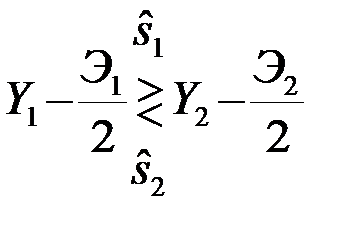. (4.3.6)

Наибольший практический интерес представляют два частных случая задачи различения: различение сигналов с одинаковыми энергиями и различение нулевого и ненулевого сигналов.

Задача различения сигналов с одинаковыми энергиями моделирует ряд практических ситуаций и, в частности, прием сигналов КИМ ЧМ и КИМ ФМ. В этом случае оптимальный алгоритм различения (6) преобразуется в

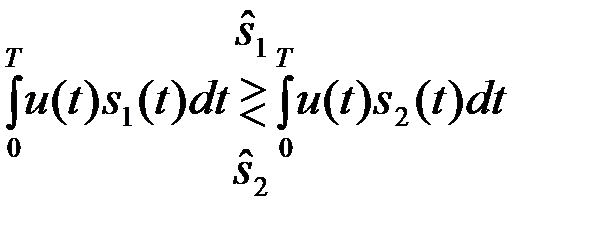. (4.3.7)

Оптимальная система должна сформировать и сравнить между собой два корреляционных интеграла (5).

Структурная схема соответствующего оптимального РПрУ приведена на рис.4.2. Это первая конкретная схема оптимальной системы, полученная нами на основании теоретического исследования без каких-либо предвзятых идей о ее структуре. Именно в этом состоит основное достоинство и привлекательность метода статистической оптимизации при синтезе систем. Так как принимаемые колебания u(t) в современных РПрУ имеют очень маленькую мощность, практические соображения требуют введения усиления в канал приема. Последнее отражено в схеме введением одинаковых коэффициентов усиления K в оба канала. Усиление, особенно СВЧ, производится, как правило, с преобразованием частоты. С точки зрения теории РТС - это второстепенные операции, которые определяются состоянием техники приема. Существенным является то, что в конечном счете оптимальная система должна сформировать два корреляционных интеграла (осуществить операции(5)) и сравнить между собой (Сх.Ср. - схема сравнения) полученные числа Y₁ и Y₂.

Алгоритм (7) и рис.4.2. непосредственно определяют структуру системы с сигналами КИМ ЧМ, для которых характерно равенство энергий. Для систем с сигналами КИМ ФМ, кроме равенства энергий характерно, что сигналы отличаются друг от друга только знаком (или сдвигом по фазе на )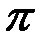

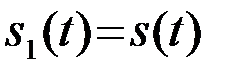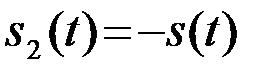, , (4.3.8)

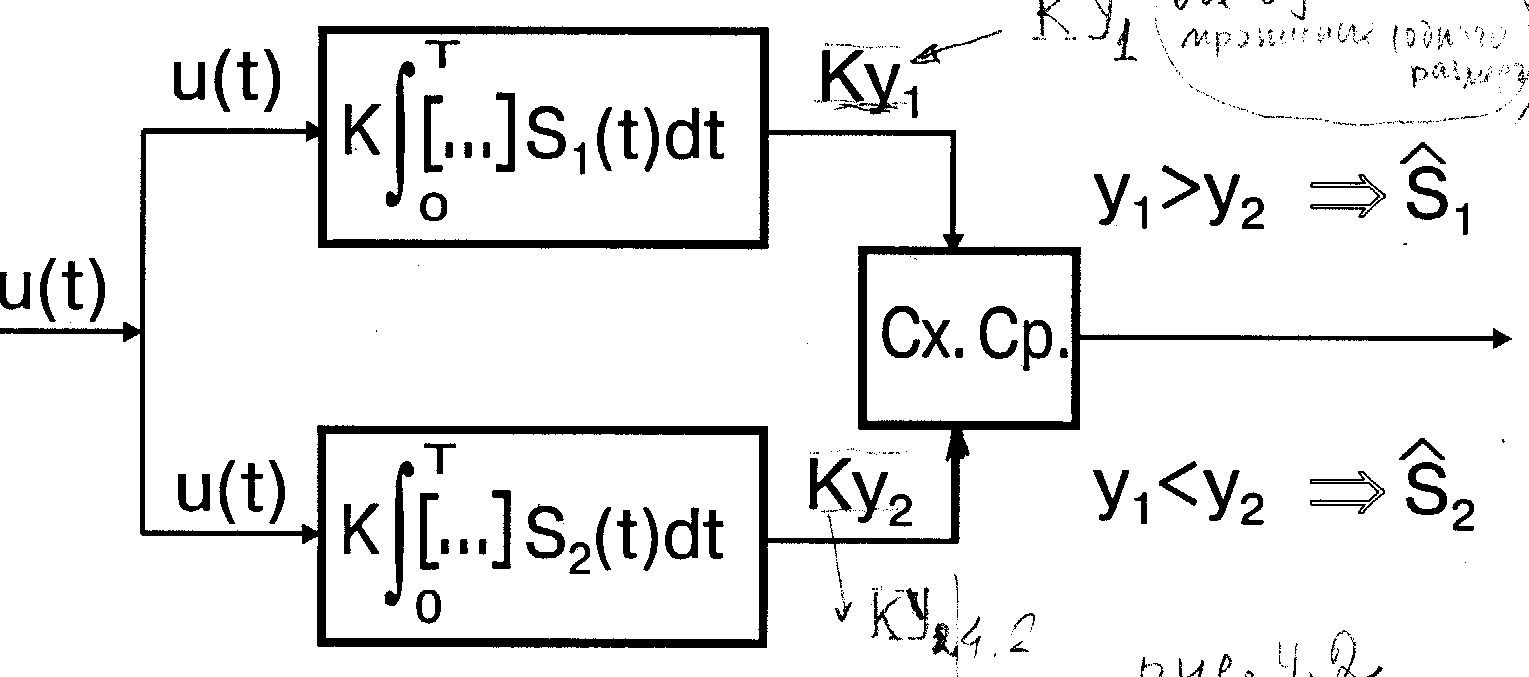
Рис. 4.2

При этом оптимальный алгоритм решения (7)

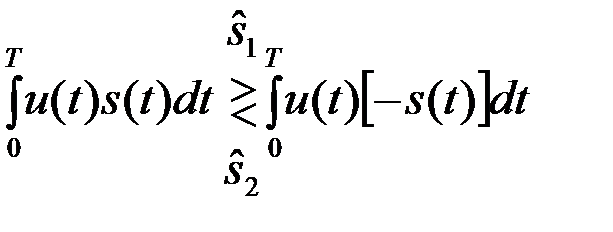
может быть преобразован к таком виду

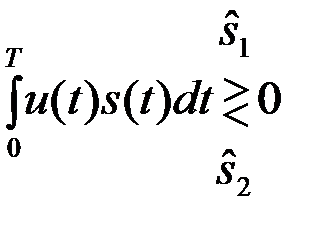. (4.3.9)

Следовательно, оптимальная система обработки должна формировать корреляционный интеграл

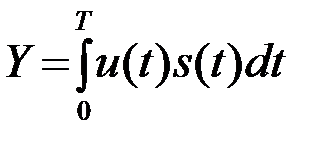(4.3.10)

и сравнивать его с порогом Y_п=0. Структурная схема устройства показана на рис. 4.3. Вместо схемы сравнения (Сх.Ср) используется пороговое устройство ПУ с пороговым уровнем Y_п=0. На выходе ПУ принимается решение 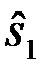, если Y>Y_п=0 и, 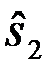, если Y<Y_п=0.

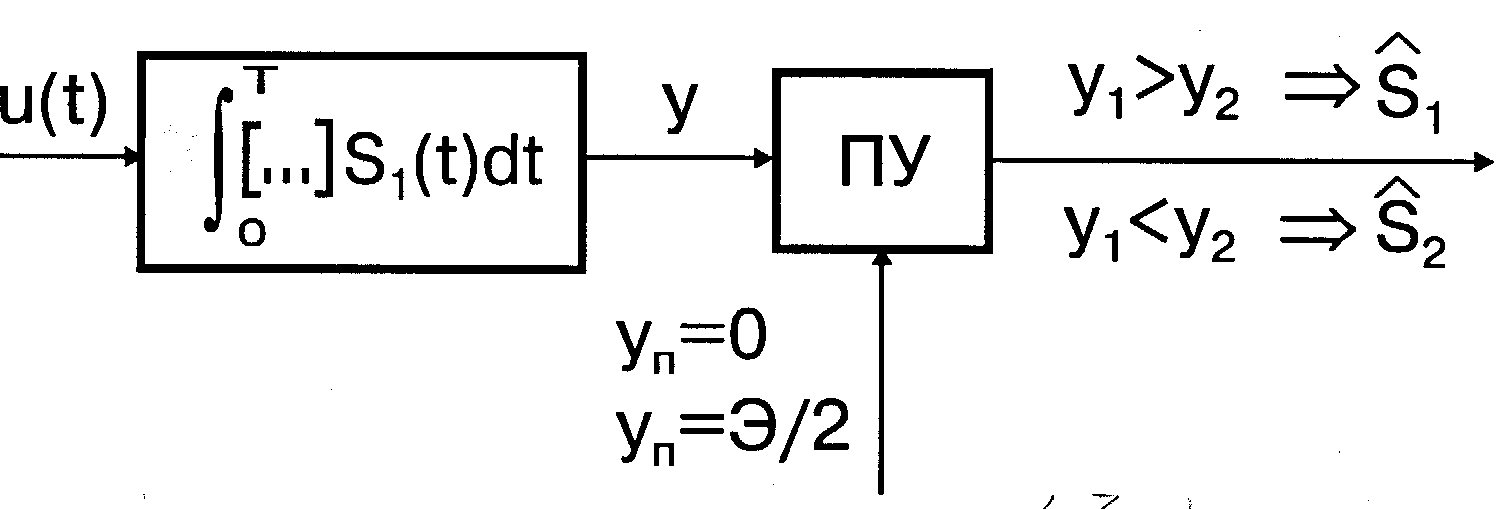
Рис. 4.3

При различении нулевого и ненулевого сигналов характерно равенство нулю одного из сигналов, положим

s₂(t)=0, Э₂=0, Y₂=0, а s₁(t)=s(t), Э₁=Э, Y₁=Y.

Оптимальный алгоритм решени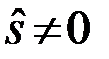й или 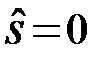согласно (6) принимает вид

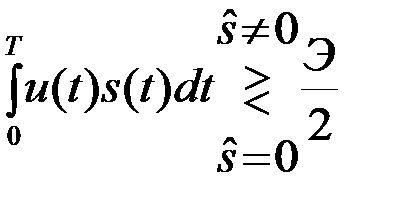. (4.3.11)

Это значит, что оптимальная система должна формировать корреляционный интеграл, стоящий в левой части неравенства (11) и сравнивать его с априорно известным порогом Y_п=0,5Э. Структурная схема оптимальной системы обработки имеет вид, подобный схеме рис.4.3. Отличие состоит лишь в величине порогового уровня Y_п. Принимается решение о наличии ненулевого сигнала, если Y>Y_п=0,5Э и наоборот.

Приведенное рассмотрение позволяет заключить, что при различении полностью известных сигналов основной (существенной) процедурой в системе оптимальной обработки наблюдений является формирование корреляционных интегралов принимаемого колебания {u(t),tÎ(0,T)} с образцами полезных сигналов, которые могут поступить на вход системы. Эта же процедура с небольшими изменениями окажется основной во многих других системах оптимальной обработки принимаемых колебаний. Поэтому представляет интерес рассмотреть практические методы формирования корреляционных интегралов.