Спектральное представление стационарных случайных процессов

Реализации стационарного СП x(t,w) по определению однородны на интервале tÎ(-¥,¥), и, следовательно, имеют неограниченную энергию 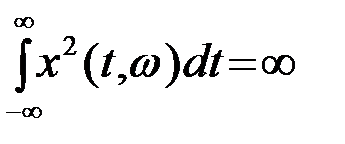. Ограниченной является средняя по времени мощность реализации x(t,w)

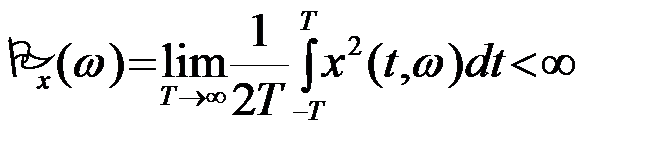.(3.5.1)

Для таких процессов можно определить спектр реализации g_x(f,w)=F{x(t,w)}. Расчет корреляционной функции 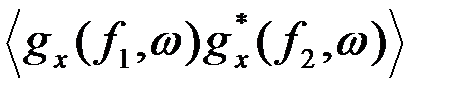показывает (см. пример 3.5.4), что случайный спектр g_x(f,w) является d - коррелированной нестационарной функцией частоты с неограниченной дисперсией, т.е. принадлежит к классу обобщенных функций.

В практических задачах используются усеченные реализации стационарных СП, отличные от нуля на конечном интервале tÎ(-T,T) (или 0£t£T)

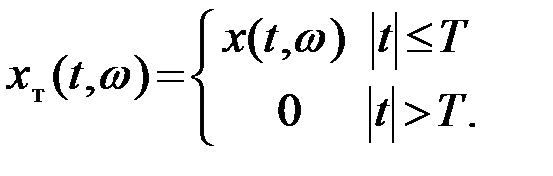(3.5.2)

Спектр усеченной реализации

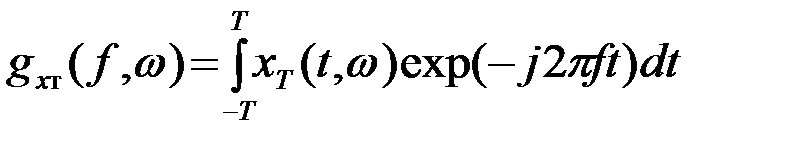(3.5.3)

является обычной функцией и может быть использован, например, для определения реакции линейной системы на воздействие данной реализации x_т(t,w). Однако спектр 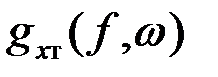не является характеристикой процесса X(t)={x_т(t,w), wÎW} в целом, так как для различных реализаций он получается различным. Кроме того, он изменяется при изменении интервала T.

Наиболее целесообразным, оказалось, характеризовать спектральные свойства стационарного СП распределением его мощности (1) на оси частот f(-¥,¥). Определим эту характеристику, для чего выразим среднюю мощность P_x(w) реализации x(t,w) стационарного, неэргодического, СП X(t) через спектр 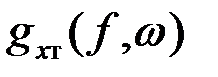усеченной реализации

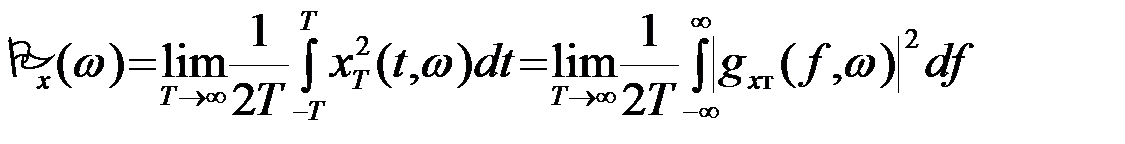. (3.5.4)

Изменив в сходящемся интеграле (4) порядок интегрирования и перехода к пределу, введем обозначение

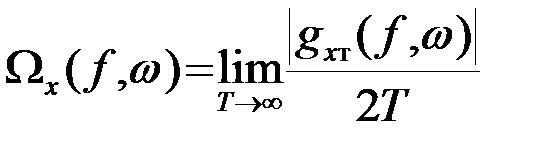.(3.5.5)

В результате получим

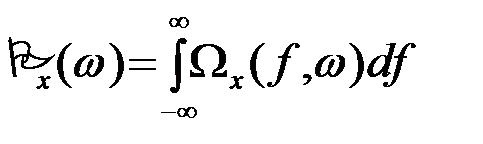. (5.5.6)

Функция W_x(f,w) имеет ясный физический смысл - это спектральная плотность мощности p_x(w) конкретной реализации x(t,w), т.е. средняя мощность реализации, приходящаяся на 1Гц полосы частот на данной частоте f. Часть мощности реализации (1), сосредоточенной в спектре в произвольной полосе fÎ(f₁, f₂ ) определяется интегралом

.

Спектральная плотность мощности W_x(f,w) является характеристикой реализации и для различных реализаций она различна (рис.3.8 штриховые линии). Заметим, что для эргодических СП средняя мощность для всех реализаций одинаковая P_x(w)=P_x . Однако спектральная плотность мощности W_x(f,w) при этом для различных реализаций остается различной. Иначе говоря, для эргодических СП эргодическим свойством обладает не спектр W_x(f,w), а интеграл (6) от этой функции.

Рис.3.8

Для получения спектральной плотности мощности (спектра мощности) W_x(f) процесса X(t) в целом (а не отдельной реализации) необходимо произвести усреднение W_x(f,w) по ансамблю реализаций (рис.3.8 сплошная линия)

.(3.5.7)

Ученые А.Я.Хинчин и Н.Винер независимо установили, что спектральная плотность мощности W_x(f) стационарного СП X(t) и его основная характеристика - корреляционная функция R_x(t) взаимно однозначно связаны между собой преобразованием Фурье (теорема Хинчина-Винера). Для доказательства этой теоремы преобразуем, принимая во внимание (3), выражение (7) для спектральной плотности W_x(f), полагая, что x(t,w) – реализации центрированного СП,

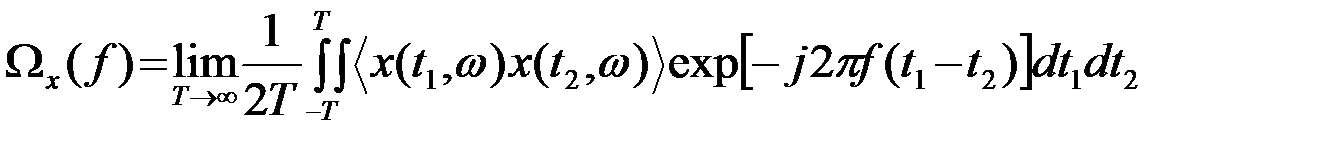. (3.5.8)

Производим замену переменных (якобиан преобразования равен 1)

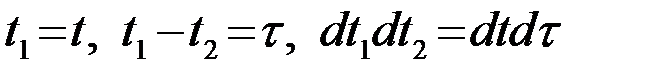(3.5.9)

и соответствующее преобразование области интегрирования (t₁,t₂)Î(-T,T) (рис.3.9).

Рис. 3.9

На рисунке зафиксированы характерные точки областей 1, 2, 3, 4. Интегрирование ведется сначала по заштрихованным полоскам (по t) - внутренний интеграл, затем по t - внешний интеграл

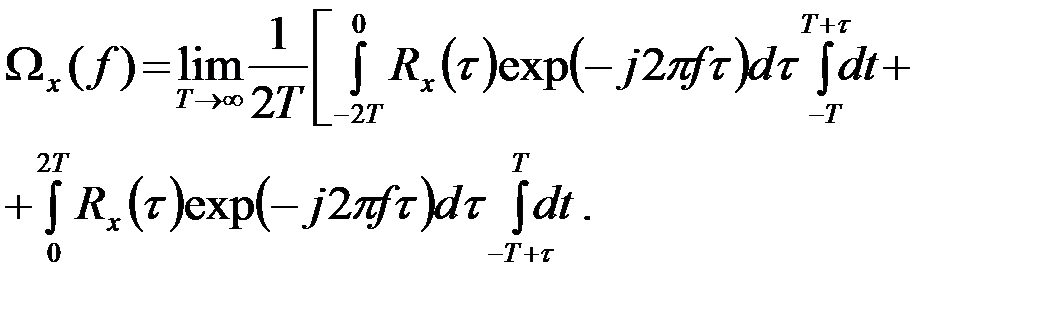(3.5.10)

После интегрирования по t (10) можно представить одним интегралом

.(3.5.11)

Функция Y(t,T)=[1-|t|/(2T)], |t|£2T, входящая в (11), показана на рис.3.10. При T®¥ Y(t,T)®1. В результате получаем утверждение теоремы. Корреляционная функция R_x(t) - стационарного СП и его спектральная плотность (мощности) W_x(f) представляют пару преобразований Фурье

. (3.5.12)

. (3.5.13)

Рис. 3.10

В соответствии с определением (7) спектральная плотность стационарного СП W_x(f) является положительной четной функцией. При использовании экспоненциального базиса спектр W_x(f) определяется на всей оси частот fÎ(-f, f) и называется двусторонним спектром. Физический спектр, непосредственно измеряемый, определяется в базисе гармонических функций только на положительной полуоси частот fÎ(0, f) и называется односторонним спектром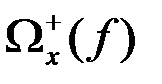

. (3.5.14)

Для нецентрированных стационарных СП в (8) и далее корреляционная функция , что приводит к выражению для спектральной плотности нецентрированного процесса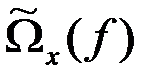

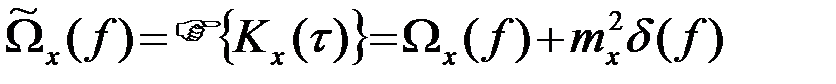, (3.5.15)

которая отличается от (12) наличием спектральной линии на нулевой частоте с мощностью .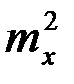

Таким образом, в рамках корреляционной теории в качестве основной характеристики стационарного СП X(t) вместо корреляционной функции R_x(t) может использоваться спектральная плотность W_x(f). Если процесс, кроме того, гауссовский, то функция W_x(f) так же как и R_x(t) полностью определяет центрированный стационарный СП. Для нецентрированных процессов требуется еще задание m_x.

Пример 3.5.1. Определить корреляционную функцию стационарного СП с равномерным ограниченным спектром мощности

.(3.5.16)

N₀ - односторонняя (N₀/2 – двусторонняя) спектральная плотность мощности, являющаяся основной характеристикой процесса с равномерным спектром.

Полная мощность (дисперсия) процесса

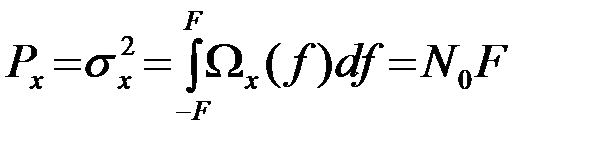.(3.5.17)

Корреляционная функция

(3.5.18)

совпадает (с точностью до коэффициента N₀F) с нулевой функцией отсчетов g₀(t). Корреляционная функция (18) обращается в нуль в точках t_k=k/(2F), k=±1,±2,... Это значит, что сечения процесса X(t) и X[t+k/(2F)] со спектральной плотностью (16), отстоящие друг от друга на интервал, кратный величине 1/(2F), не коррелированны (для гауссовских СП - не зависимы). Время корреляции процесса величина порядка 1/(2F).

Пример 3.5.2. Определить корреляционную функцию белого шума. Белым шумом называется СП с равномерным неограниченным спектром мощности

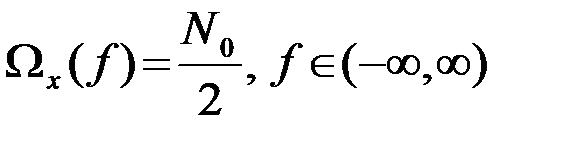.(3.5.19)

Белый шум, который можно рассматривать как предельный переход при F®¥ процесса в предыдущем примере, физически нереализуем, так как имеет неограниченную мощность. В теоретических исследованиях белый шум представляет собой удобную идеализацию процесса с равномерным спектром, ширина которого существенно превосходит полосу частот, занимаемую другими процессами, находящимися в совместном рассмотрении.

Корреляционная функция белого шума

(3.5.20)

имеет вид d - функции. Это значит, что два сечения процесса X(t₁) и X(t₂) в любые несовпадающие моменты отсчета t₁¹t₂ не коррелированны (для гауссовских процессов не зависимы). Поэтому белый шум называют также процессом с некоррелированными значениями или некоррелированным СП. Соответственно белый шум можно рассматривать как идеализацию процесса с очень малым временем корреляции. В статистической теории РТС широко используется модель в виде гауссовского СП с характеристиками (19), (20), называемая гауссовским белым шумом (ГБШ).

Пример 3.5.3. Определить корреляционную функцию стационарного СП с гауссовским (колокольным) спектром мощности

, (3.5.21)

где 2F - эффективная ширина спектра, определяемая как основание прямоугольника П(f/2F) равновеликого (с равной площадью) экспоненте exp[-pf²/(2F)²]. Уровень отсчета полосы 2F равен exp(-p/4)=0,46.

Корреляционная функция (повторяется расчет, приведенный в примере 2.2.3)

(3.5.22)

получается также гауссовской. Эффективная длительность корреляционной функции (удвоенное время корреляции t_k) равна 1/(2F).

Пример 3.5.4. Определить основные характеристики случайной функции g_x(f,w) - спектра реализации стационарного СП x(t,w). Математическое ожидание g_x(f,w) =0, а корреляционная функция

после подстановки t₁ =t, t₂ =t-t, получается равной

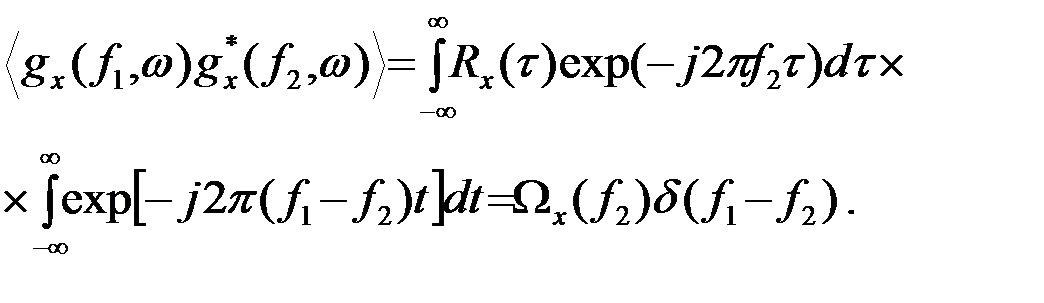(3.5.23)

Следовательно, спектр g_x(f,w) представляет собой нестационарную случайную функцию (корреляционная функция зависит от двух переменных f₁ и f₂), которая бесконечно быстро флюктуирует и имеет бесконечно большую дисперсию.

Пример 3.5.5. Определить корреляционную функцию R_x(t) стационарного узкополосного СП x(t) с равномерным спектром W_x(f) (рис.3.11а)

. (3.5.24)

Принимая во внимание, что (sina–sinb)=2sin[1/2(a–b)]cos[1/2(a+b)], получаем (рис.3.11,б)

Рис. 3.11

Математические модели помех

Наблюдение, поступающее на вход приемного устройства РТС, представляет собой сумму полезного сигнала s(t,l,a), модель которого уже была изучена, и аддитивной (маскирующей) помехи n(t)

.

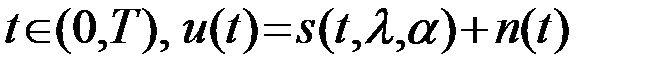Ближайшей задачей теперь является обоснование математической модели аддитивных помех n(t). В аддитивную помеху входят, во-первых, внутренние шумы аппаратуры и помехи природного происхождения: радиоизлучение Земли и атмосферы, радиоизлучение внеземного происхождения (Солнца, планет, космического пространства). Эти помехи являются гауссовскими, однородными на интервале наблюдения tÎ(0,T) и имеют сравнительно с сигналом широкий спектр.

Во-вторых, имеются аддитивные помехи иного происхождения: промышленные помехи, взаимные помехи от посторонних РТС, пассивные помехи, организованные (умышленные) помехи. В принципе каждая из этих помех может быть негауссовской. Однако на основании центральной предельной теоремы теории вероятностей в большинстве случаев можно считать, что сумма всех этих помех также стремится к гауссовскому распределению.

В результате оказалось целесообразным использовать две модели помех. Основная модель, которую будем называть основной гауссовской помехой представляет собой стационарный гауссовский СП с ограниченным или неограниченным равномерным спектром. Существенно, что полоса частот, занятая помехой, включает в себя полосу частот, занятую сигналом. Эта модель в основном описывает внутренние шумы и помехи природного происхождения, всегда присутствующие в наблюдении. В частных случаях модель может описывать некоторые помехи второй группы.

Второй моделью является общая гауссовская помеха, нестационарная или стационарная со спектром неравномерным в пределах полосы частот, занятой сигналом. Эта модель описывает большинство помех второй группы. Иногда изучается оптимизация приема на фоне негауссовских помех. Аналитический аппарат при этом значительно усложняется. В связи с этим отметим, что в американской литературе [4] утверждается: "если система хорошо спроектирована для работы на фоне гауссовских помех, то она будет хорошо работать также на фоне негауссовских помех".

Рассмотрение начнем с модели основной гауссовской помехи. В дальнейшем, следуя практике, принятой в технической литературе, будем обозначать СП и его отдельные реализации одними и теми же символами: u(t), n(t), x(t) и др.

Рис. 3.12

На рис.3.12 заштрихована область частот fÎ(f₀-F_c, f₀+F_c), занятая на положительной полуоси fÎ(0,¥) спектром принимаемого сигнала s(t,l,a). На рисунке также показан примерный вид спектра мощности помехи W_п(f). Важно, что помеха обычно имеет более широкий по сравнению с сигналом спектр и в пределах сигнальной полосы fÎ(f₀-F_c, f₀+F_c) имеет примерно постоянную спектральную интенсивность. Мешающее действие оказывают только те частотные составляющие помехи, которые попадают в полосу частот, занятую сигналом. Наоборот, частотные составляющие помехи, расположенные вне полосы частот fÎ(f₀-F_c, f₀+F_c), практически приему сигнала не препятствуют. Поэтому, выбирая математическую модель помехи, предназначенную для анализа процесса приема, не требуется точное воспроизведение этой моделью частотных составляющих, которые не попадают в полосу частот, занятую сигналом. Удобно аппроксимировать помеху n(t) гауссовским стационарным СП с равномерным ограниченным спектром (рис.3.12)

(3.6.1)

Верхняя частота спектра F может быть выбрана произвольно, но такой, что F³f₀+F_c. Ниже будет показано, что при этом конечные формулы и выводы от величины F не зависят. N₀/2 - двухсторонняя спектральная плотность, т.е. мощность идеализированной помехи, приходящаяся на каждый 1Гц полосы fÎ(-F,F), равная спектральной плотности мощности реальной помехи на несущей частоте сигнала W_п(f₀). СП такого вида рассматривался ранее (пример 3.5.1)

Модель (1) является примером идеализации, хорошо согласующейся с реальным явлением и вместе с тем существенно облегчающей математический анализ. Для дальнейшего исследования закономерностей приема сигналов на фоне помех n(t) нужно ввести меру вероятности различных реализаций СП n(t) на интервале наблюдения tÎ(0,T). Перейдем к определению этой меры.

Если спектр мощности W_п(f) стационарного в широком смысле СП n(t) ограничен полосой |f|£F, в частности, имеет вид (1), то реализации этого процесса представимы рядом Котельникова

.(3.6.1)

Особенность состоит в том, что оговоренный выше вид спектра (1) относится не к спектру мощности W_п(f,w) реализации, представленной рядом (2), а к математическому ожиданию этого спектра W_п(f,w) =W_п(f) - к спектру мощности процесса. Вследствие этой особенности равенство (2) является не абсолютным, как для детерминированных процессов, а соблюдается в вероятностном (в среднеквадратическом) смысле: математическое ожидание квадрата ошибки - разности между левой и правой частями (2), равно нулю.

Для представления реализации СП n(t) на большом, но конечном интервале наблюдения tÎ(0,T) с достаточной для технических приложений точностью, как и для детерминированных процессов, можно пользоваться усеченным рядом (2), в котором сохраняются только те отсчеты, которые попадают в интервал наблюдения tÎ(0,T). Таким образом, реализация {n(t),tÎ(0,T)} однозначно определяется совокупностью своих отсчетов n₀=n(0), n₁=n(T₀), ..., n_m=n(mT₀) т.е. вектором , где T₀=1/2F, m=2FT. Появление реализации {n(t), tÎ(0,T)} тождественно появлению совокупности отсчетов 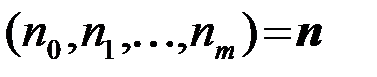. Поэтому ПВ реализации {n(t),tÎ(0,T)}, обозначаемая далее P₀[n(t)], совпадает с ПВ p₀(n) вектора n, т.е. с (m+1)-мерной ПВ процесса n(t)

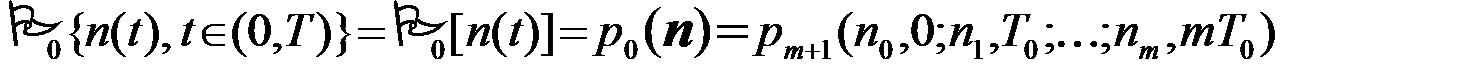.(3.6.3)

Аналитическое выражение для ПВ (3) легко получить, если учесть, что гауссовская помеха n(t) согласно выбранной модели имеет корреляционную функцию (пример 3.5.1)

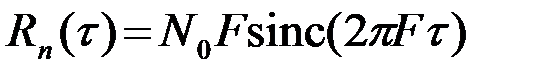.(3.6.4)

При этом все фигурирующие в (3) отсчеты помехи n₀,n₁,...,n_m, сдвинутые друг относительно друга на интервалы, кратные T₀=1/2F, статистически независимы. Поэтому ПВ (m+1)-го порядка равна произведению ПВ 1-го порядка p₁(×)

.

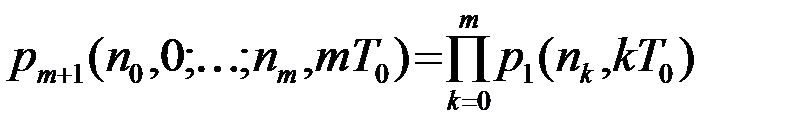Так как ПВ центированной гауссовской случайной величины n_k с дисперсией , равна

,

то

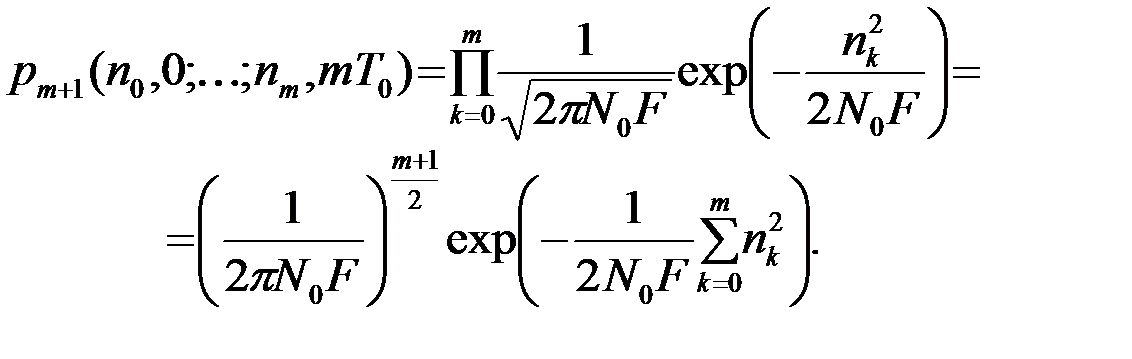
Принимая во внимание, что энергия Э_n реализации {n(t), tÎ(0,T)}

,

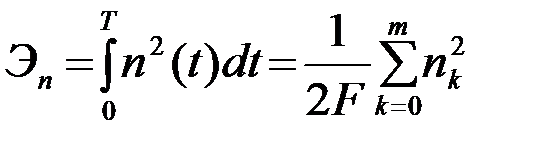окончательно получаем

, (3.6.5)

где C - независящий от реализации n(t) коэффициент

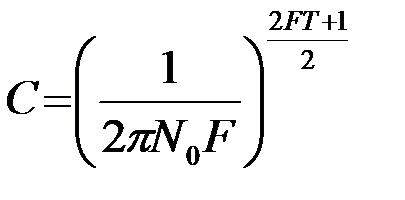.(3.6.6)

Выражение (5) представляет собой пример функциональной связи, ставящей в соответствие функции {n(t), tÎ(0,T)} число P₀[n(t)]=Cexp(-Э_n/N₀). Такая функциональная связь называется функционалом. Поэтому в литературе ПВ P₀[n(t)] называют функционалом ПВ помехи.

Если изменить выбранную в значительной мере произвольно верхнюю частоту F спектра помехи, то в функционале ПВ (5) изменится только величина коэффициента C. Однако в практических задачах представляет интерес не абсолютное значение ПВ P₀[n(t)], а то, во сколько раз одна реализация помехи, положим n₁(t), более или менее вероятна, чем другая - n₂(t), т.е. отношение

, (3.6.7)

которое от коэффициента C не зависит.

Часто в качестве модели помехи n(t) используется гауссовский стационарный процесс с равномерным неограниченным спектром (пример 3.5.2) - белый гауссовский шум (БГШ)

.(3.6.8)

По соображениям, приведенным выше, мешающее действие этой помехи такое же, как и СП, выбранного нами в качестве предыдущей модели. Отличие состоит лишь в том, что для белого шума верхняя частота F®¥ . Выражение для функционала ПВ остается тем же (5). Отметим, при F®¥ согласно (6) коэффициент C®0, что в соответствии с пояснениями, приведшими к (7), не препятствует решению практических задач.

При использовании в качестве модели общей гауссовской помехи функционал ПВ помехи {n(t), tÎ(0,T)} определяется корреляционной функцией R_n(t₁,t₂) в общем случае нестационарного центрированного гауссовского СП. Запишем сначала для этой помехи многомерную ПВ любого конечного порядка m. Будем считать, что m сечений n(Dt)=n₁,..,n(mDt)=n_m равномерно распределены (Dt=T/m) на интервале tÎ(0,T). Согласно(3.3.5)

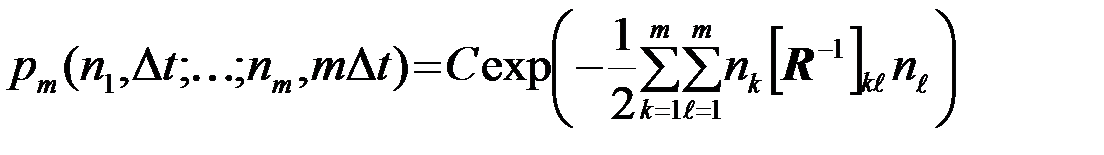, (3.6.9)

где C - коэффициент, не зависящий от реализации помехи n(t) и значений ее отсчетов n_k и n_ℓ, а [ 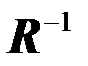]_kℓ - элементы матрицы 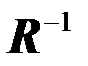, обратной к корреляционной R, с элементами R_kℓ=R_n(kDt,ℓDt) так что

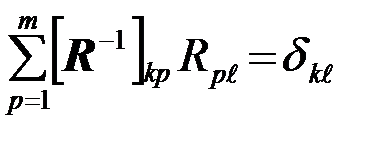.(3.6.10)

Для получения функционала ПВ P₀[n(t)] представим показатель экспоненты (9) в виде интегральной суммы и перейдем к пределу Dt®0 (m=T/Dt®¥). При этом kDt®t_k , ℓDt®t_ℓ , mDt®T и вводится обозначение

.(3.6.11)

Тогда показатель экспоненты в выражении (9) можно преобразовать в интегральную сумму

.

Функцию W(t_k,t_ℓ) называют обратной корреляционной функцией. Определяют ее из интегрального уравнения

, (3.6.12)

получаемого преобразованием (10) в интегральную сумму

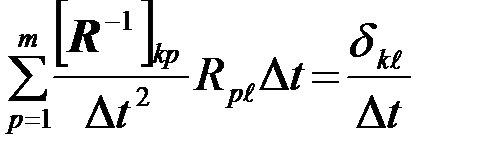
и перехода к пределу Dt®0 (m®¥ ), d_kℓ/Dt®d(t_k-t_ℓ).

В результате функционал ПВ общей гауссовской помехи принимает вид (переменные интегрирования t_k и t_ℓ заменены на t₁ и t₂)

.(3.6.13)

В частном случае, когда моделью помехи является белый шум R_n(t₁,t₂)=N₀/2d(t₁-t₂), решением интегрального уравнения для обратной корреляционной функции

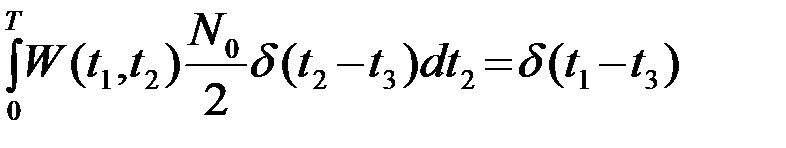
является

(3.6.14)

и функционал ПВ помехи (13) преобразуется, как и следовало ожидать, в (5).

Формула (13) статистически исчерпывающе определяет модель общей гауссовской помехи, а также модели многих сигналов. Однако пользование этой моделью затруднено тем, что обратная корреляционная функция W(t₁,t₂) может быть определена аналитически в замкнутом виде из уравнения (12) для ограниченного вида функций корреляции R_n(t₁,t₂). В дальнейшем будем считать, что помеха n(t) имеет равномерный ограниченный или неограниченный спектр мощности и пользоваться моделью основной гауссовской помехи, т.е. функционалом ПВ (5). Только в некоторых специальных случаях будем пользоваться общей гауссовской моделью (13).

Функция правдоподобия

Запишем сначала функционал ПВ P{u(t), tÎ(0,T)}=P[u(t)], называемый для краткости ПВ процесса

,

представляющего собой сумму помехи n(t) с ПВ P₀[n(t)], например, (3.6.5) и детерминированного процесса s(t). Процесс u(t) отличается от гауссовской помехи n(t) только тем, что имеет ненулевое математическое ожидание u(t) =s(t). Соответственно центрированное значение процесса u(t) совпадает с помехой 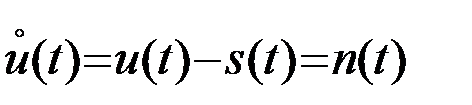. Поэтому, если реализация процесса u(t) приняла некоторый конкретный вид , то это значит, что реализация помехи приняла вид . Следовательно, ПВ того, что процесс u(t) примет конкретное значение равна ПВ того, что помеха n(t) примет значение 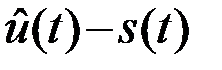, т.е. 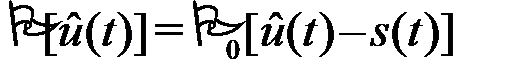. Последнее равенство верно для любой реализации процесса u(t). Поэтому знак ^ можно опустить и окончательно записать

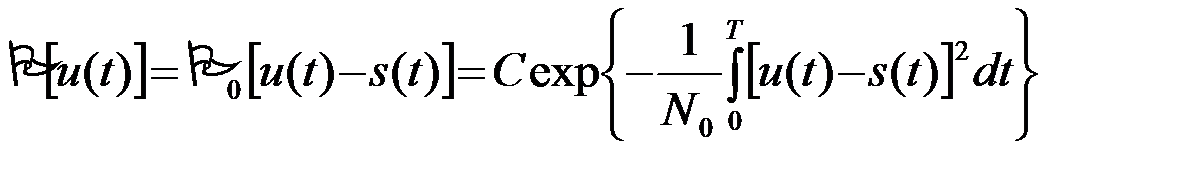. (3.7.2)

Таким образом, ПВ P[u(t)] гауссовского СП (1) с ненулевым математическим ожиданием u(t) =s(t) выражается через ПВ помехи P₀[u(t)-s(t)].

Перейдем теперь к реальной модели наблюдения u(t). Будем считать, что наблюдение равно сумме

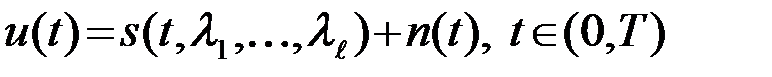,(3.7.3)

основной гауссовской помехи n(t) и сигнала s(t,l₁,..,l_ℓ), являющегося квазидетерминированным СП, зависящим от совокупности случайных параметров l₁,...,l_ℓ . В данном случае не существенно, что собой представляют параметры l₁,...,l_ℓ , в частности, какие из них информационные, а какие - несущественные. Важно, что l₁,...,l_ℓ это вся совокупность случайных параметров сигнала (неизвестных на приемной стороне), и задание этой совокупности l₁,...,l_ℓ полностью определяет реализацию сигнала. При этом сигнал s(t,l₁,...,l_ℓ) становится детерминированной функцией времени s(t) и мы возвращаемся к модели (1).

Пример 3.7.1. Запишем простейший принимаемый радиолокационный сигнал

.(3.7.4)

Параметры излучаемого сигнала t_и и f₀ заранее известны. Неизвестными на приемной стороне и воспринимаемые как случайные величины l₁, l₂, l₃ являются параметры t, e, j . Задание конкретных значений этих параметров преобразует (3) в детерминированную функцию времени s(t).

Таким образом, при условии, что заданы конкретные значения всех случайных параметров сигнала l₁,...,l_ℓ функция s(t,l₁,...,l_ℓ) становится детерминированной функцией времени, равной математическому ожиданию наблюдения u(t). Поэтому условная ПВ P[u(t)/l₁,...,l_ℓ] реализации процесса u(t) при условии, что все параметры сигнала фиксированы и равны данным значениям l₁,...,l_ℓ представляет собой ПВ процесса u(t) вида (1) с математическим ожиданием u(t) =s(t, l₁,...,l_ℓ). В результате получаем

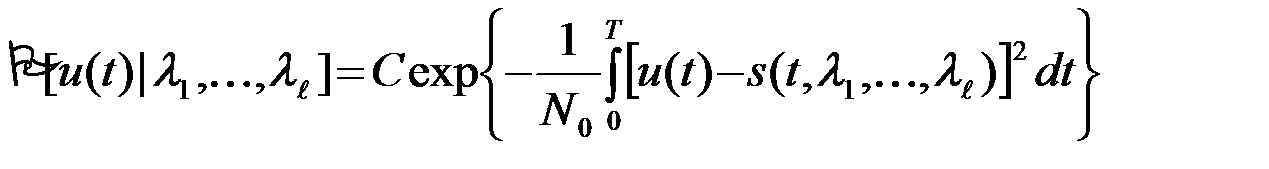. (3.7.5)

ПВ P[u(t)|l₁,...,l_ℓ], как это видно из (4), представляет собой функцию наблюдения u(t) и параметров l₁,...,l_ℓ. Если значение параметров l₁,...,l_ℓ зафиксировано (обусловлено), то P[u(t)|l₁,...,l_ℓ] - условная ПВ. Если, наоборот, зафиксировать наблюдение {u(t),tÎ(0,T)}, то P[u(t)|l₁,...,l_ℓ] является функцией параметров l₁,...,l_ℓ и называется функцией правдоподобия (параметров l₁,...,l_ℓ). Смысл названия в том, что функция P[u(t)|l₁,...,l_ℓ] характеризует относительную правдоподобность предположения, что наблюдение u(t) образовалось из сигнала с данной совокупностью параметров l₁,...,l_ℓ. Если P[u(t)|l₁⁽¹⁾,...,l_ℓ⁽¹⁾]>P[u(t)|l₁⁽²⁾,...,l_ℓ⁽²⁾], то более правдоподобно предположение, что наблюдение {u(t),tÎ(0,T)} образовалось из сигнала s(t,l₁⁽¹⁾,...,l_ℓ⁽¹⁾), чем из сигнала s(t,l₁⁽²⁾,...,l_ℓ⁽²⁾).

Совершенно аналогично, если гауссовская помеха n(t) имеет произвольную корреляционную функцию, отличную от 0,5N₀d(t₁-t₂) или N₀Fsinc2pF(t₁-t₂), то условная ПВ наблюдения u(t) (функция правдоподобия) P[u(t)|l₁,...,l_ℓ] определяется ПВ (3.6.13)

(3.7.6)

Во многих практически важных случаях требуется функция правдоподобия не для всей совокупности параметров сигнала l₁,...,l_ℓ , а только для информационных. Положим, что в принимаемом сигнале s(t, l₁,...,l_ℓ) только l₁ и l₂ - информационные параметры, тогда как все остальные параметры l₃,...,l_ℓ - несущественные. Требуется определить функцию правдоподобия информационных параметров P[u(t)|l₁,l₂]. Особенность этой ситуации состоит в том, что имеется аналитическое выражение (4) или (5) для случая, когда зафиксирована вся совокупность параметров сигнала l₁,...,l_ℓ и сигнал превращается в детерминированную функцию s(t), являющуюся математическим ожиданием СП u(t). Однако необходимо определить условную ПВ наблюдения u(t) при условии, что зафиксированы параметры l₁ и l₂, тогда как остальные параметры l₃,...,l_ℓ могут иметь произвольные значения. Задача эта решается непосредственным применением правил теории вероятностей. Совместную ПВ несущественных параметров l₃,...,l_ℓ обозначим p(l₃,...,l_ℓ). Тогда условная (обусловлено значение l₁ и l₂) совместная ПВ наблюдения u(t) и параметров l₃,...,l_ℓ согласно формуле произведения вероятностей равна

. (3.7.6)

Далее, пользуясь условием согласованности многомерной ПВ, т.е. усредняя (6) по параметрам l₃,...,l_ℓ находим интересующую нас ПВ

или

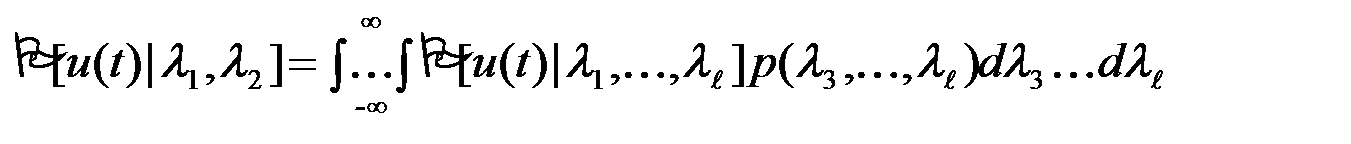. (3.7.7)

Следовательно, функция правдоподобия информационных параметров определяется по функции правдоподобия для всей совокупности случайных параметров сигнала путем статистического усреднения последней, т.е. усреднения с весом p(l₃,...,l_ℓ), по несущественным параметрам l₃,...,l_ℓ .

Приведем еще один пример определения функции правдоподобия для наблюдения

,

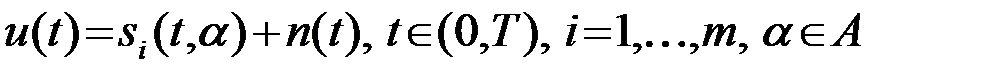в котором информационным является дискретный параметр i=1,..m, а a - несущественный параметр (возможно векторный), принадлежащий непрерывному интервалу A. Иначе говоря, сигнал на входе может иметь вид одной из m заранее известных функций s₁(t,a),...,s_m(t,a) времени t и параметра a. Требуется записать функцию правдоподобия для сигнала s_i (для информационного параметра i). На основании изложенного

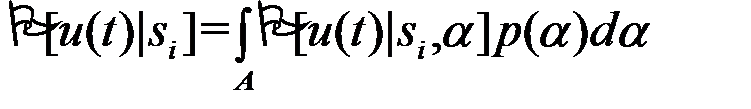
или для основной гауссовской помехи

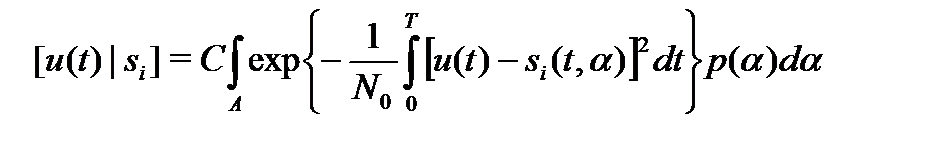. (3.7.8)

В дальнейшем статистический синтез и анализ РТС основывается в значительной мере на использовании различных условных функционалов ПВ наблюдения - функций правдоподобия.

РАЗЛИЧЕНИЕ СИГНАЛОВ

В главе на примере приема цифровых сигналов в РТС изучается общая методика и математический аппарат принятия оптимальных статистических решений и анализа качества таких решений. Обсуждаются схемные реализации оптимальных решающих систем - систем различения сигналов.