Спектральное представление сигналов

Анализ и синтез сигналов и элементов РТС можно проводить во временной или в частотной области. Переход из одной области в другую выражается преобразованием Фурье ( ), которое определим следующими формулами

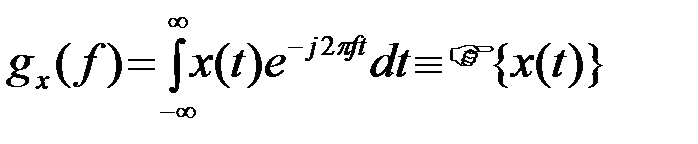, (2.2.1)

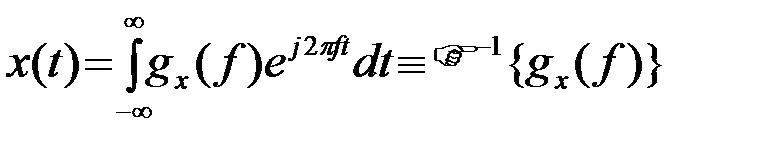. (2.2.2)

Символы {} и ^-1{} обозначают прямое и обратное преобразование Фурье, которые в принятом виде (1)-(2) отличаются только знаком в показателе экспоненты, f[Гц] - циклическая частота. Используется также круговая частота 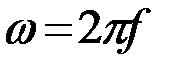[рад/с]. При этом в (2) появляется коэффициент 1/(2p).g_x(f) - спектральная плотность функции x(t), называемая кратко спектром процесса x(t). В общем случае спектр g_x(f) - комплексная функция, определенная при fÎ(-¥,¥) и включающая в себя амплитудный спектр |g_x(f)| и фазовый спектр 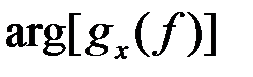процесса x(t). Принимая во внимание, что

,

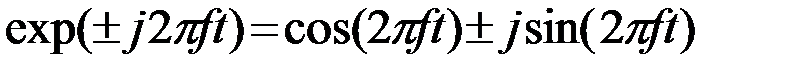из (1) следует, что спектр g_x(f) вещественного процесса x(t) на отрицательной полуоси fÎ(-¥,0) однозначно определяется спектром на положительной полуоси fÎ(0,¥) (звездочка * означает комплексное сопряжение)

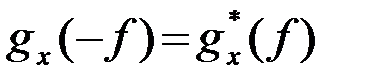(2.2.3)

или

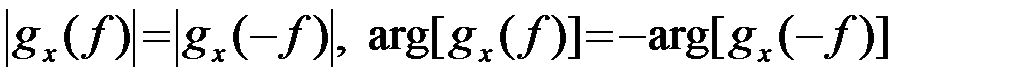(2.2.4)

Поэтому (2) можно преобразовать так, чтобы интегрирование проводилось только по положительным частотам fÎ(0,¥)

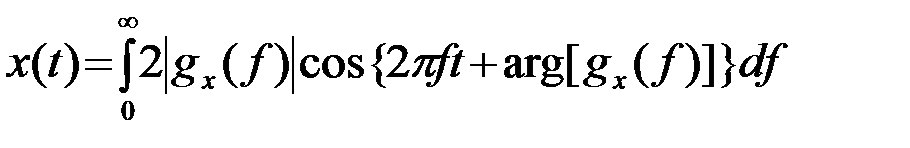(2.2.5)

Симметрия прямого и обратного преобразования Фурье при этом теряется. Преобразование (2) представляет процесс x(t) суммой (пределом суммы) экспонент с комплексными амплитудами 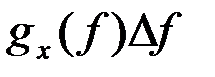, тогда как (5) - пределом суммы косинусоид с положительными частотами fÎ(0,¥). Преобразование (5) более физично. Однако использование (2), не меняя существа дела, обеспечивает удобство и простоту математического аппарата.

Если x(t) четная вещественная функция, то спектр g_x(f) также x четная вещественная функция, а прямое и обратное преобразование Фурье представляют собой тождественное cos - преобразование, так как

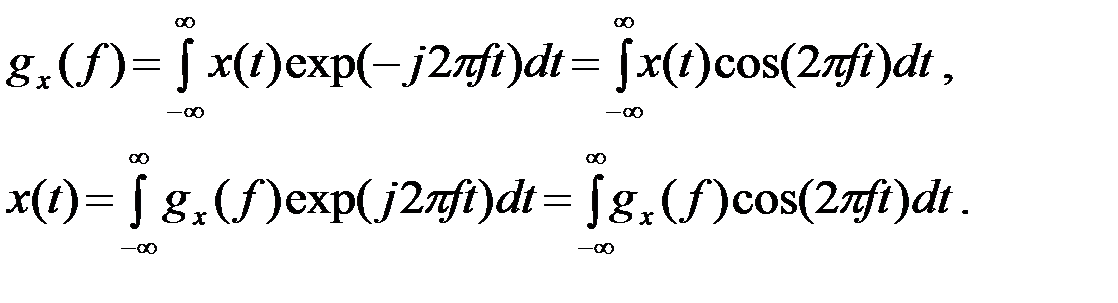(2.2.6)

Согласно (1), (2) функции x(t) и g_x(f) представляют, x собой пару взаимно-однозначных преобразований (преобразований Фурье), что будет записываться

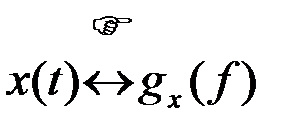. (2.2.7)

В классической математике преобразование Фурье (1), (2) было определено для функций абсолютно интегрируемых или функций с интегрируемым квадратом

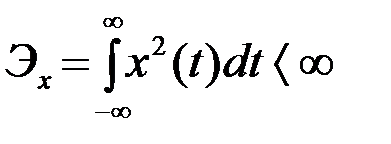. (2.2.8)

Интеграл (8) называется энергией процесса x(t) и обозначается Э_x. Если x(t) - напряжение или ток, то (8) действительно полная энергия процесса на нагрузке в 1Ом.

В настоящее время область применения преобразования Фурье (1), (2) со строгостью, приемлемой для физиков, расширена на функции с неограниченной энергией (с неограниченным интегралом (8)) такие как: sin(2p¦t), единичный скачок (x(t)=0 при t<0, x(t)=1 при t³0), 1/t, tⁿ (n<¥), дельта-функция d(t) и др. Мы этой возможностью будем пользоваться.

Положим заданы g₁(f)= {x₁(t)}, g₂(f)= {x₂(t)} и требуется определить преобразование Фурье {x₁(t)x₂(t)} произведения x₁(t)x₂(t)

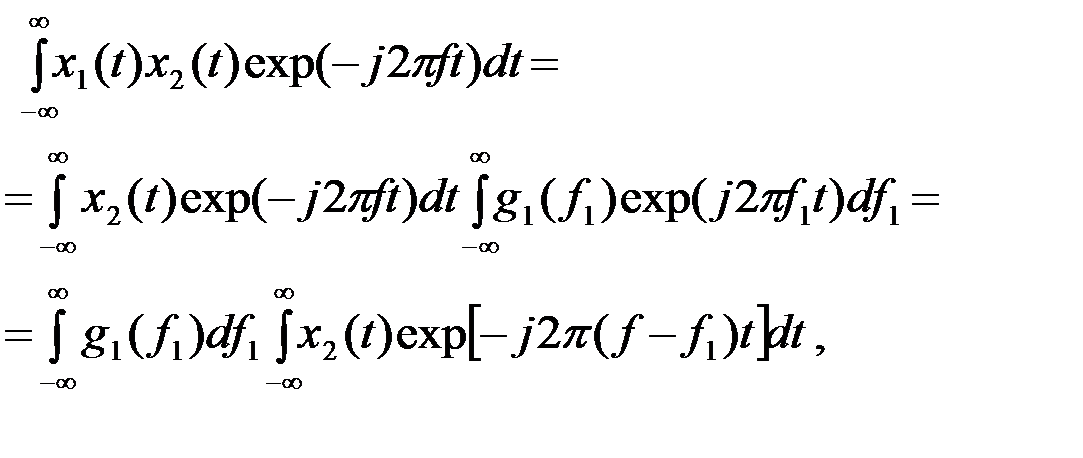
откуда

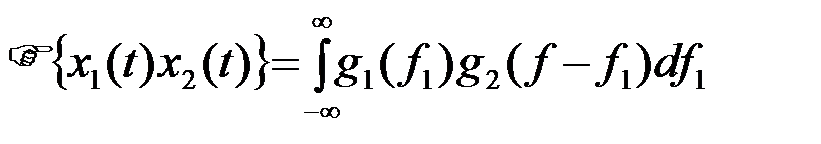. (2.2.9)

Интеграл вида (9) называется в математике сверткой функций g₁ и g₂ и обозначается символом *

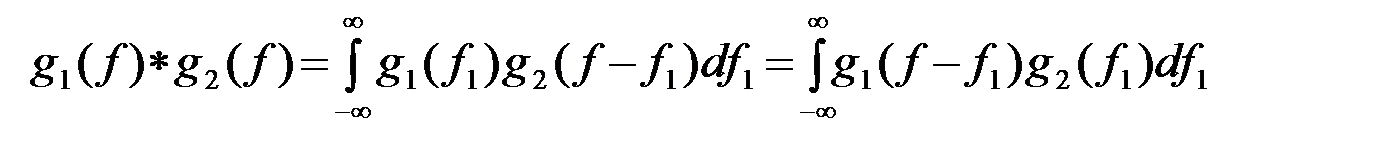. (2.2.10)

Итак

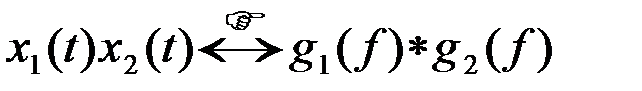. (2.2.11)

Совершенно аналогично

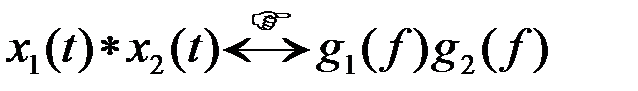. (2.2.12)

Произведению двух функций в одной области соответствует свертка функций в другой.

Частным случаем приведенных формул являются формулы Парсеваля. При f=0 согласно (9)

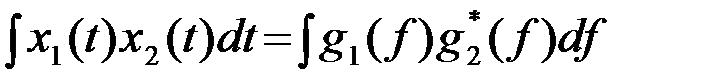. (2.2.13)

Если x₁=x₂ =x и соответственно g₁ =g₂ =g, то

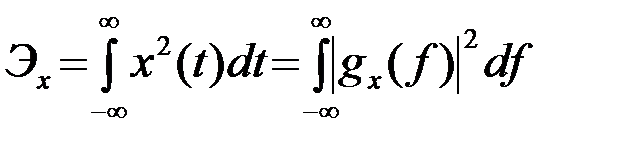. (2.2.14)

Это значит, что функция 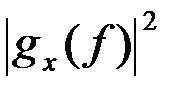является спектральной плотностью энергии сигнала, то есть определяет энергию спектральных составляющих, приходящихся на 1Гц спектра сигнала на частоте f.

Приведем еще одно полезное соотношение. Так как согласно (1) 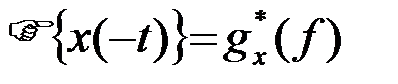, то

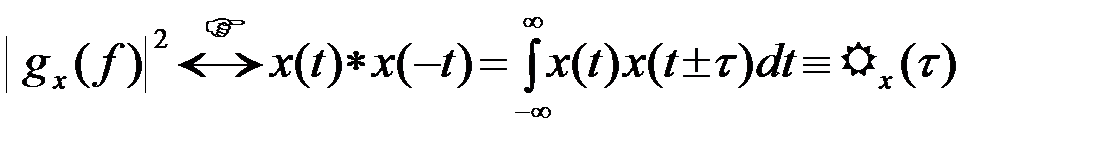, (2.2.15)

где R_x(t ) - так называемая (временная) корреляционная функция сигнала x(t) с ограниченной энергией.

Пример 2.2.1. Введем обозначение П(t) для прямоугольного импульса с единичными амплитудой и длительностью

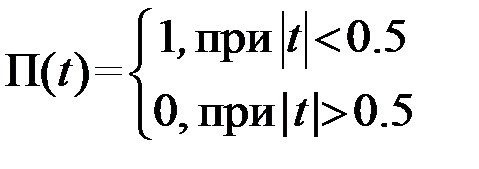(2.2.16)

и найдем спектр импульса с произвольными параметрами (рис.2.1)

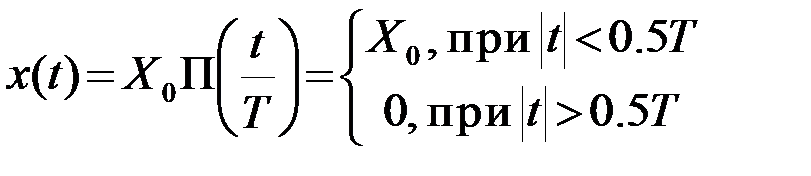. (2.2.17)

Рассматриваемый сигнал является четной функцией, поэтому

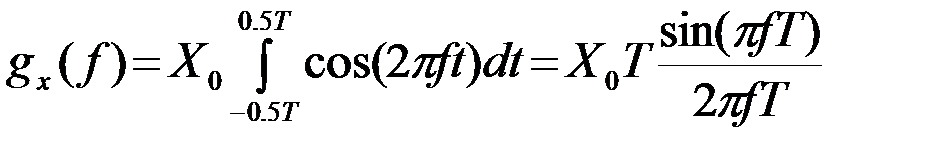. (2.2.18)

Аналогично, для прямоугольного спектра 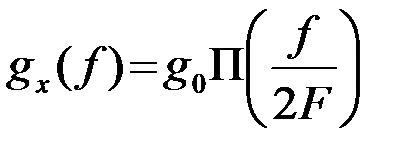(рис.2.2) соответствуящая функция времени будет

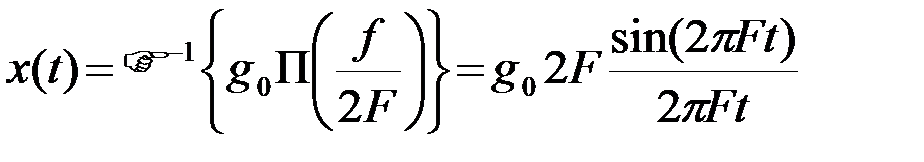. (2.2.19)

В частном случае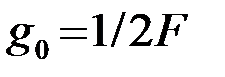

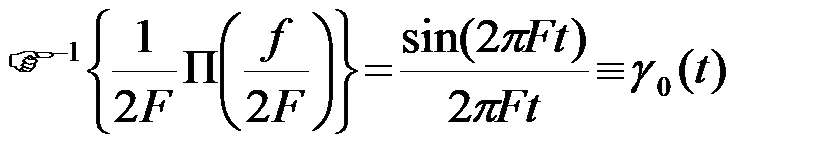. (2.2.20)

Функция g₀(t), называемая нулевой функцией отсчетов, широко используется в дальнейшем. Запишем для нее некоторые соотношения.

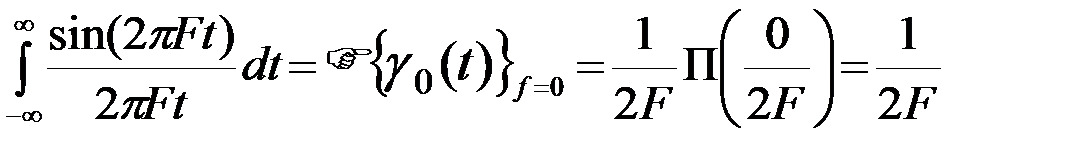. (2.2.21)

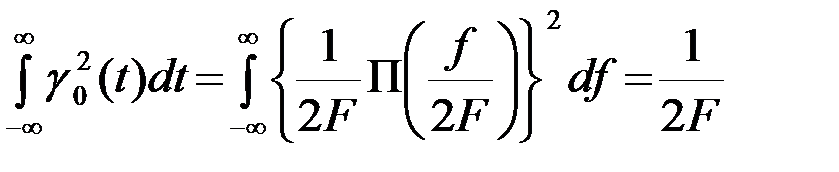. (2.2.22)

Наконец

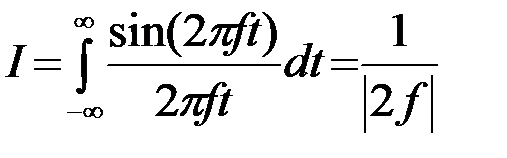. (2.2.23)

Соотношение (23) получается из (21) заменой FÎ(0,¥) на f, f(-¥,¥). При этом согласно (21)

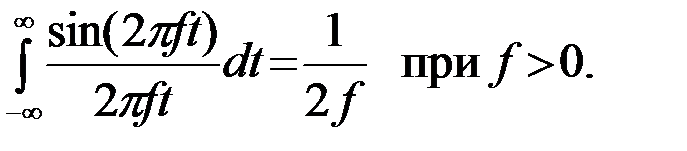
Из четности по параметру f подынтегрального выражения следует четность самого интеграла (23) 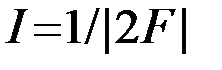. Функция sin(x)/x так часто появляется в теории сигналов, что для нее ввели специальное обозначение

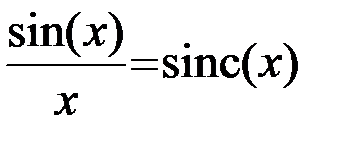. (2.2.24)

Пример 2.2.2. Определим спектр функции 1/(pt), используемой в дальнейшем при преобразовании Гильберта

.

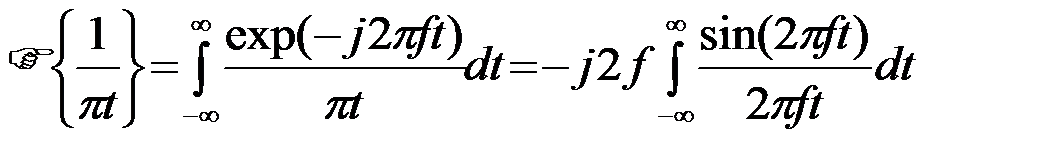Принимая во внимание (23), получаем

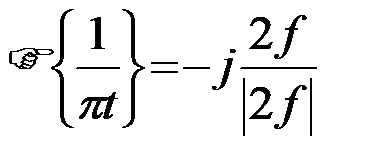. (2.2.25)

Функция 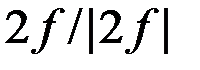имеет значение 1 при f>0 и -1 при f<0. Такая функция называется знаковой и обозначается символом sgn (signum)

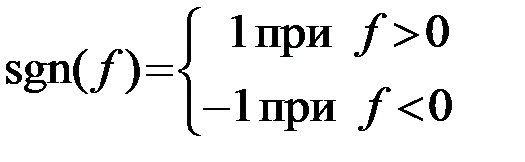. (2.2.26)

Следовательно

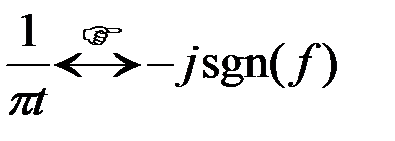. (2.2.27)

Пример 2.2.3. В теории сигналов в качестве модели импульса наряду с прямоугольным используется так называемый гауссовский импульс, имеющий вид гауссовской кривой (рис.2.3)

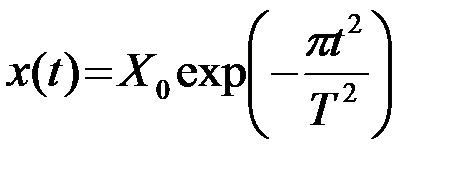. (2.2.28)

Здесь T - эффективная длительность импульса

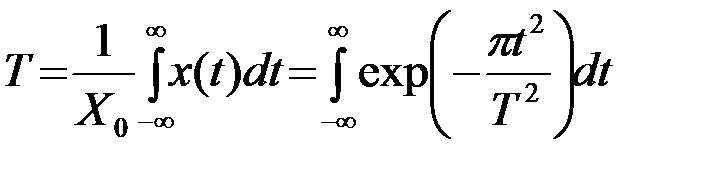(2.2.29)

равная основанию прямоугольника, равновеликого (по амплитуде и площади) гауссовскому импульсу. При этом получается, что длительность T импульса (8) отсчитывается на уровне 0.46.

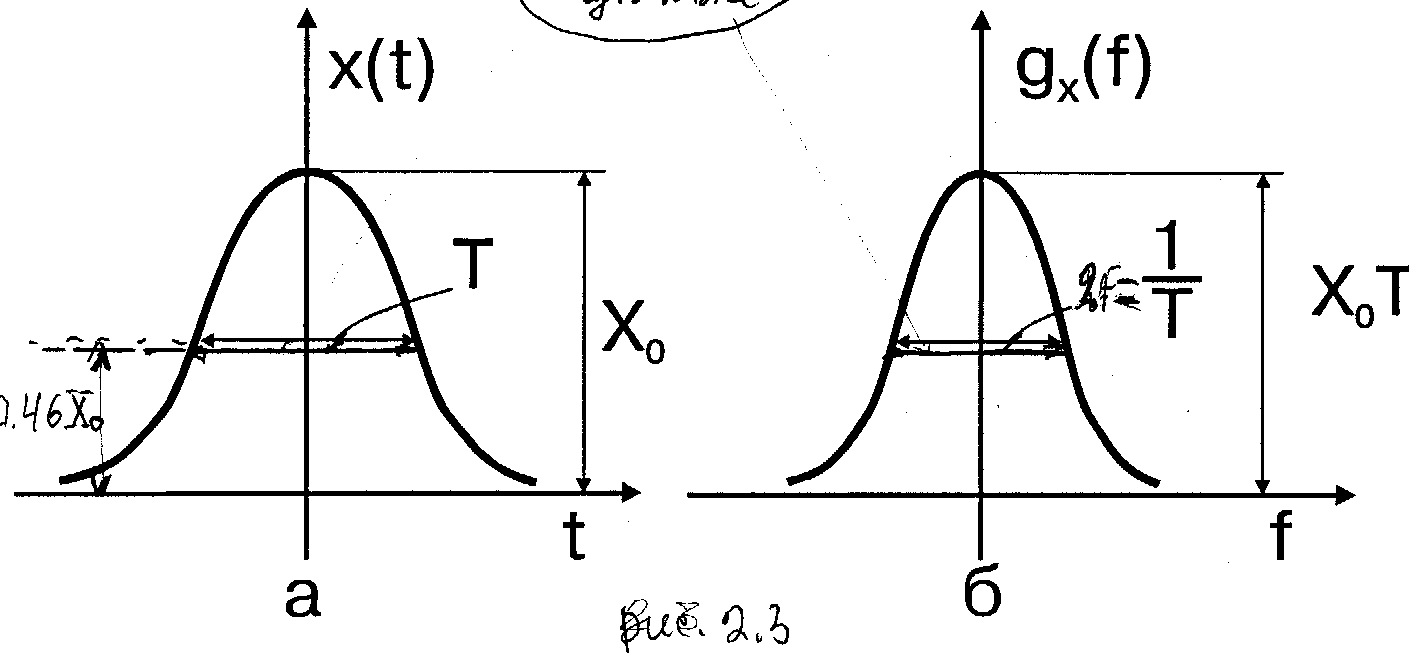
Определим спектр гауссовского импульса

.

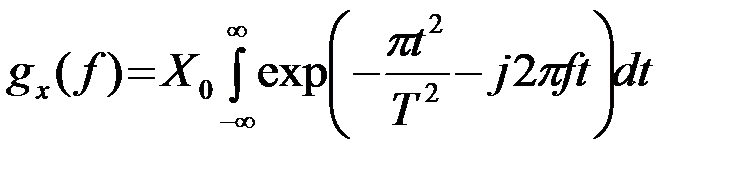Дополняя показатель степени экспоненты до полного квадрата, прибавляя и вычитая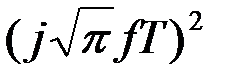

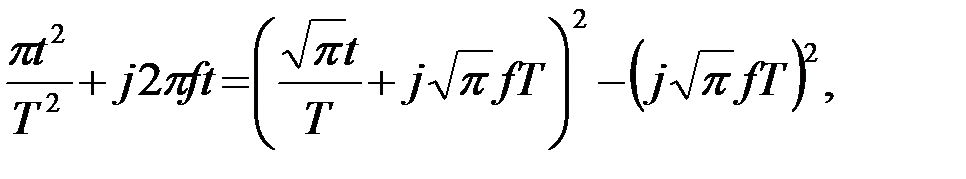
получаем

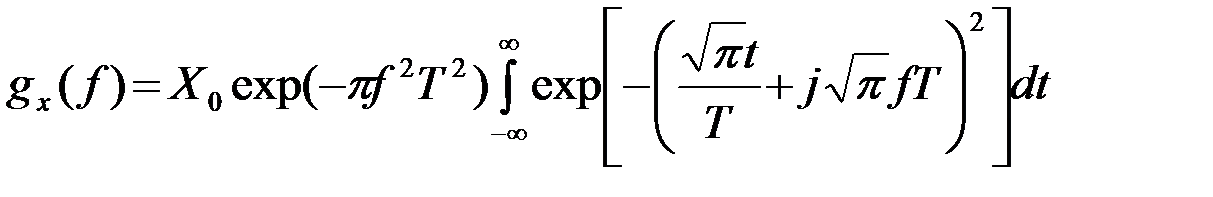
и

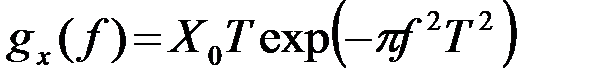*). (2.2.30)

Спектр гауссовского импульса также имеет гауссовскую форму. Ширина спектра (на уровне 0.46) 2F=1/T.

Дельта-функция

Дельта-функцию часто определяют соотношением

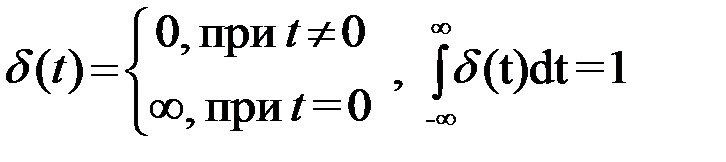. (2.3.1)

В инженерной практике дельта-функция используется в качестве асимптотической или идеализированной модели короткого импульса d_D(t) с единичной площадью. Форма импульса длительности D произвольная. В большинстве случаев

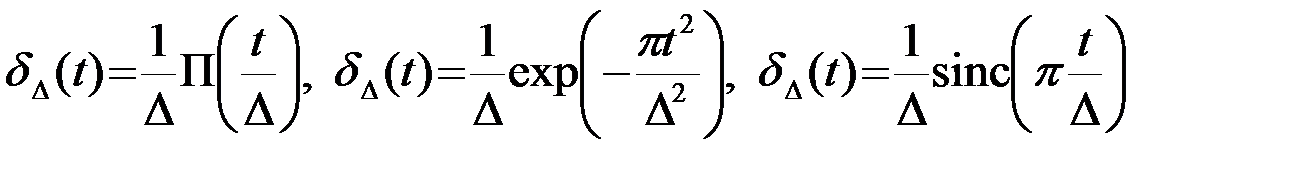. (2.3.2)

При этом

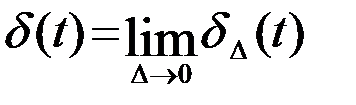. (2.3.3)

Математически функция определяется своими значениями соответствующими каждому значению аргумента. Ни (1), ни (3) с этим определением не согласуется. Функции (1) и (3) везде равны нулю, кроме одной точки, в которой обращаются в бесконечность - задают величину не имеющую строгого определения. В настоящее время в математике используется широкий класс функций, называемых обобщенными функциями, которые определяются не их значениями, а тем, что они делают при воздействии на обычные функции (или на динамические системы). Функция d(t) является примером обобщенной функции.

Из (1) или (3) следует, что произведение d(t-t₀) на произвольную непрерывную в t=t₀ функцию j(t) равно: 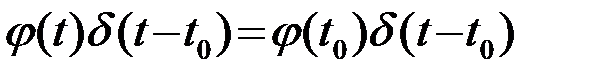и представляет собой модель короткого импульса с площадью j(t₀). Поэтому

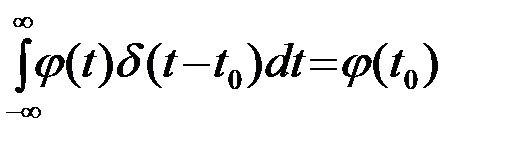. (2.3.4)

Формула (4) выражает фильтрующее свойство дельта-функции, которое является для нее определяющим. Таким образом, дельта-функция d(t) является обобщенной функцией, свертка которой с произвольной непрерывной функцией j(t) воспроизводит последнюю

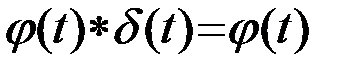. (2.3.5)

Спектр g(f) функции d(t) согласно (4)

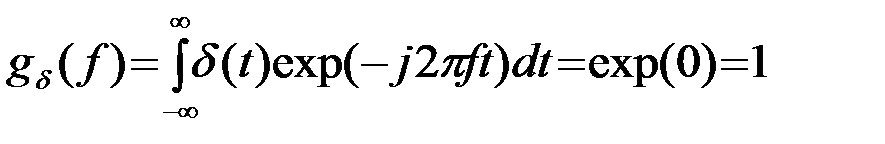(2.3.6)

имеет постоянное значение, равное 1 при fÎ(-¥,¥).

Обратное преобразование

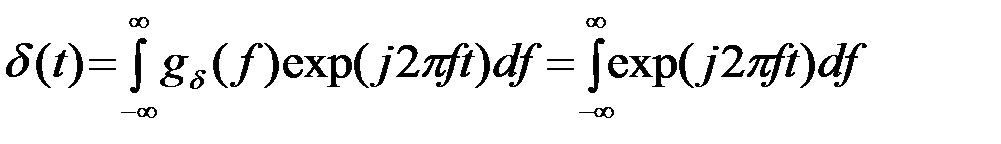.(2.3.7)

Обобщая (7), можно записать

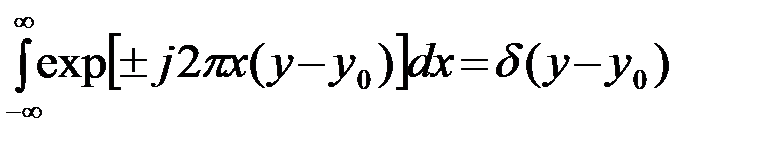.(2.3.8)

Последнее выражение используется для определения спектральной плотности гармонических и периодических сигналов (сигналов с неограниченной энергией).

Гармонический сигнал tÎ(-¥,¥)

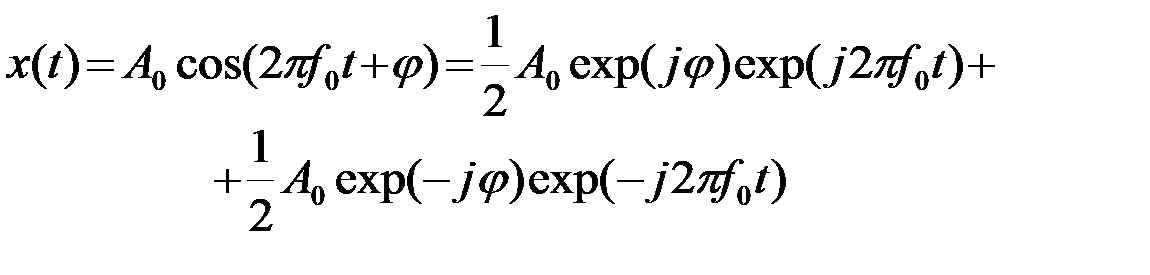. (2.3.9)

Согласно (8)

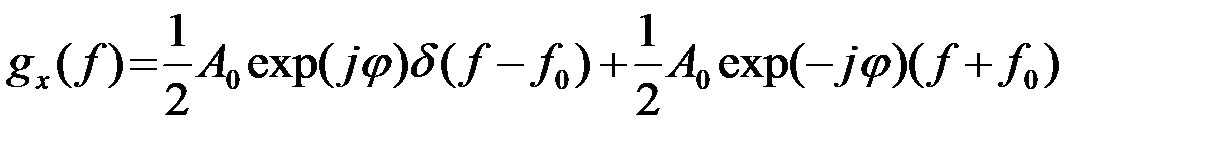. (2.3.10)

Положим, что функция с ограниченной энергией x₀(t) равна нулю вне интервала tÎ(-0.5T, 0.5T), т.е. x₀(t)=0 при |t|>0.5T. Периодический сигнал с периодом повторения T₀ >T

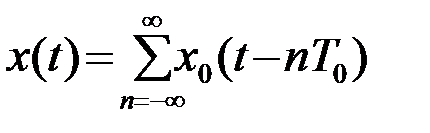(2.3.11)

может быть представлен рядом Фурье

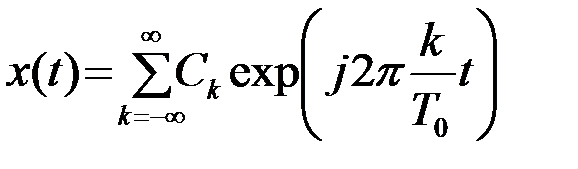.(2.3.12)

Коеффициенты ряда равны

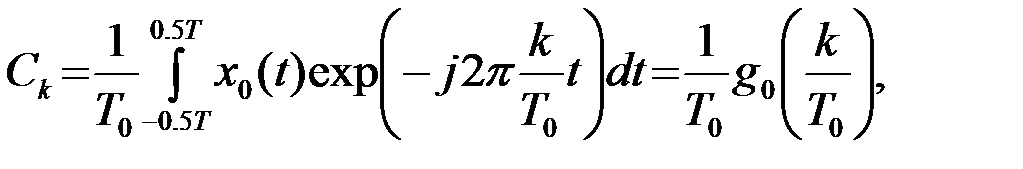(2.3.13)

где g₀(f) - спектр сигнала x₀(t):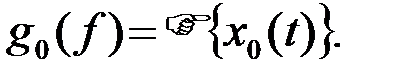

Спектральная плотность периодического процесса (12), (13) согласно (8) является дискретной функцией

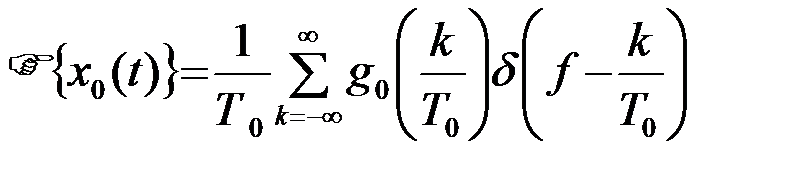.(2.3.14)

Заметим, что функция x₀(t) с конечным носителем, т.е. отличная от нуля на конечном интервале |t|£0.5T , также может быть представлена на этом интервале рядом Фурье (12). При этом выражение (12) при подстановке в него (13) может рассматриваться как интегральная сумма, которая при 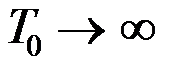переходит в преобразование Фурье (2.2.2), а (13) - в (2.2.1).

Пример 2.3.1. В теории сигналов широко используется дискретизирующая (или решетчатая) функция (рис.2.4)

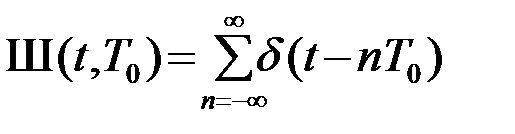.(2.3.15)

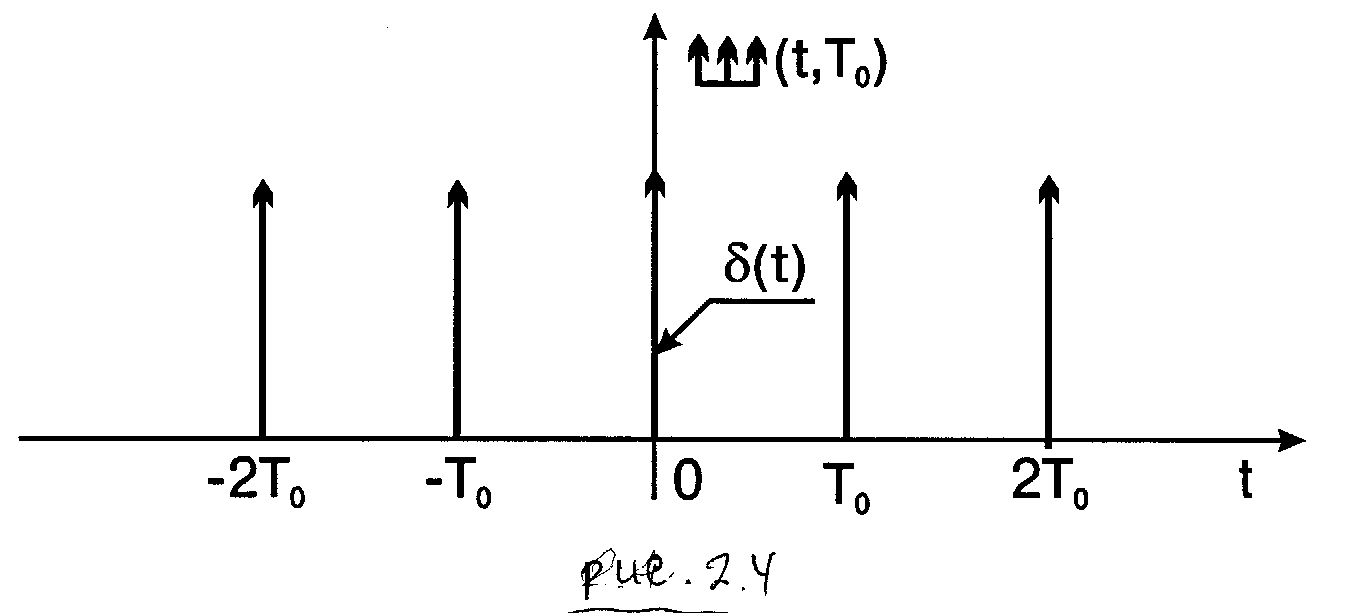
Определим преобразование Фурье дискретизирующего процесса 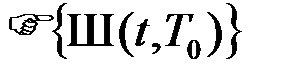. Если принять в (11) x₀(t)=d(t) и соответственно 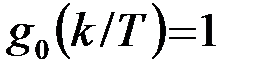, то согласно (14)

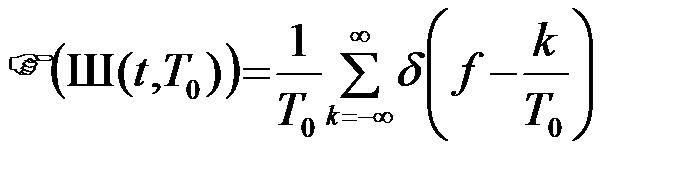(2.3.16)

или

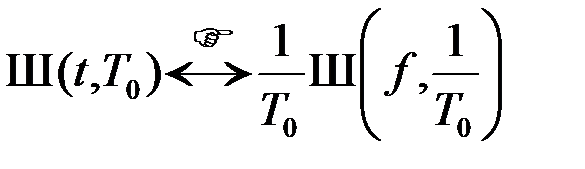.(2.3.17)

Дискретизирующий процесс во временной области с периодом T₀ и дискретизирующий процесс в частотной области с периодом 1/T₀ (с точностью до коэффициента 1/T₀) являются парой преобразований Фурье. Закономерность (16), (17) можно было получить, представляя рядом Фурье (12) непосредственно дискретизирующую функцию Ш(t,T₀).

Аналитический сигнал

Модель узкополосного радиосигнала (ширина спектра сигнала значительно меньше несущей частоты f₀) обычно представляют в виде квазигармонического колебния

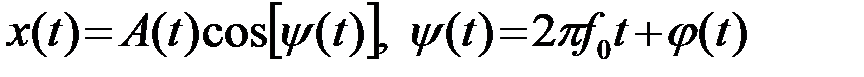.(2.4.1)

с медленно изменяющимися по сравнению с cos(2pf₀t) огибающей A(t) и фазой j(t). Полная фаза колебаний обозначена y(t). Такое определение сигнала x(t) является неоднозначным без дополнительных условий. В (1) можно выбрать различные пары сомножителей A(t) и cosy(t), дающие одно и то же произведение x(t). Разумно потребовать, чтобы модель (1) была такой, при которой огибающая A(t) и сигнал x(t) не пересекались, а точки их касания имели общую касательную. В теоретических и прикладных исследованиях оказалось удобным использовать модель аналитического (комплексного) сигнала 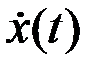. При этом физический (реальный) сигнал x(t) является вещественной частью аналитического 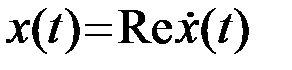. Мнимая часть аналитического сигнала 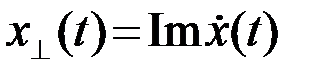задается преобразованием Гильберта реального сигнала

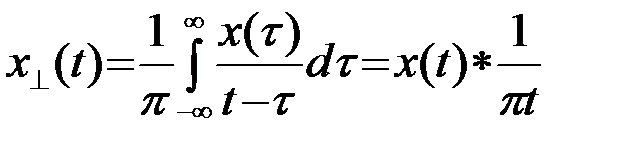.(2.4.2)

Это обеспечивает однозначное определение огибающей A(t) и полной фазы y(t)=2p¦₀t+j(t) сигнала (1), соответствующее физическим представлениям о них

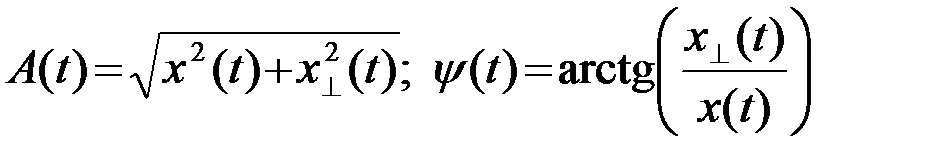.(2.4.3)

Аналитический сигнал при этом можно записать в показательной форме

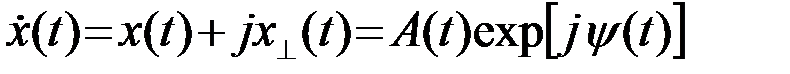(2.4.4)

и представить на комплексной плоскости (рис.2.5) в виде вектора с переменной длиной A(t), вращающегося с переменной угловой скоростью w(t) [рад/с]

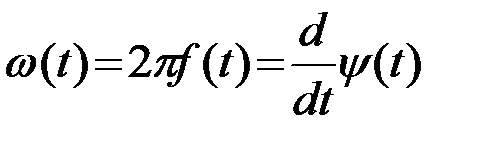.(2.4.5)

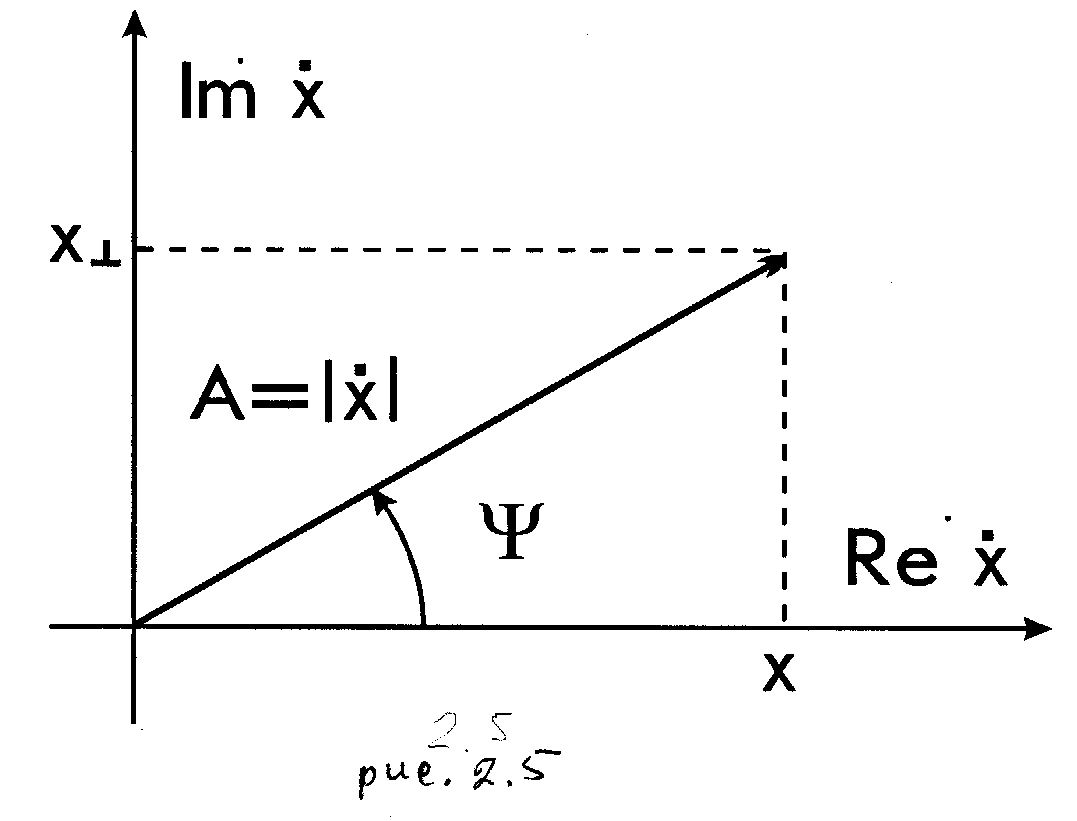
После неоднозначного в общем случае выбора несущей частоты f₀ (выбор обсуждается ниже), однозначно определяется закон изменения начальной фазы

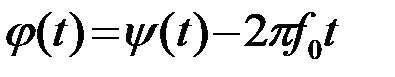.(2.4.6)

Рассматриваемые сигналы 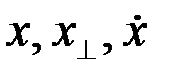(рис.2.5) выражаются при этом формулами: (1),

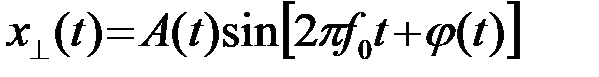(2.4.7)

и

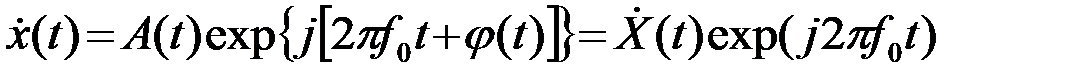, (2.4.8)

где 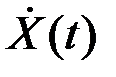- комплексная огибающая сигнала

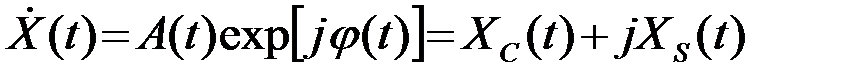.(2.4.9)

Сопряженный (по Гильберту) сигнал x_^(t) (7) сдвинут по фазе на p/2 по отношению к реальному сигналу x(t) (1) и называется квадратурным сигналом, а X_c(t) и X_s(t) - вещественная и мнимая составляющие комплексной огибающей 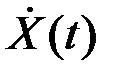, называемые также квадратурными составляющими комплексной огибающей 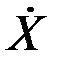. Представление радиосигналов на комплексной плоскости (рис.2.5) широко используются при изучении модулированных сигналов (АМ, ФМ, ЧМ).

Рассмотрим еще представление аналитического сигнала 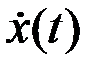в частотной области. Положим спектр реального сигнала g_x(f)= {x(t)} (точнее его модуль |g_x(f)|) имеет вид, изображенный на рис.2.6а.

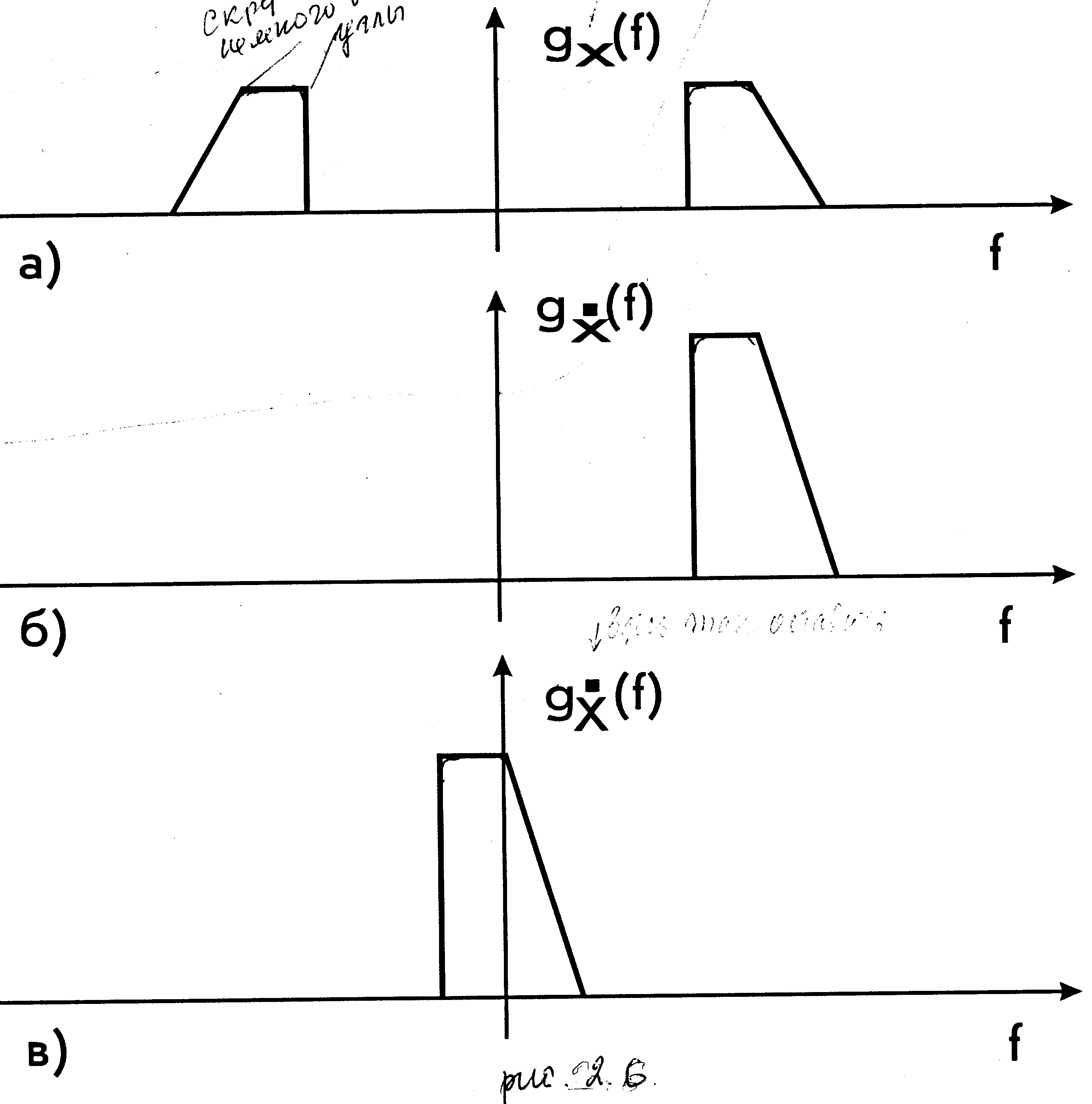
В соответствии с общей закономерностью его амплитудный спектр |g_x(f)| симметричен относительно оси f=0. Спектр сопряженного x сигнала x_^(t), являющегося во временной области сверткой (2), в частотной области будет равен произведению спектров {x(t)} и (2.2.27)

.

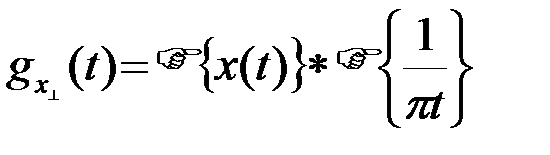Следовательно

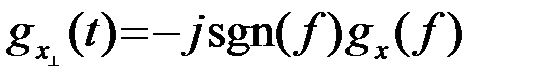.(2.4.10)

Амплитудные спектры сопряженных (квадратурных) сигналов x(t) и x_^(t) совпадают. Соответственно спектр 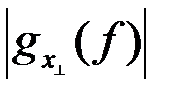совпадает с 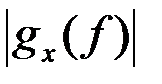, изображенным на рис. 2.6а.