ОПРЕДЕЛЕНИЕ статических ХАРАКТЕРИСТИК типовых

ЗВЕНЬЕВ И СИСТЕМЫ автоматического управления

Цель работы

Целью работы является изучение статических характеристик типовых звеньев и системы автоматического управления и методов их графического построения по заданным передаточным функциям.

Теоретическая часть

Как динамическая система, САУ может работать в одном из двух режимов – в стационарном (установившемся) и в переходном. Поэтому в общем виде порядок исследования САУ в обоих случаях включает математическое описание системы, исследование ее стационарных (установившихся) и переходных режимов.

Стационарный режим может быть статическим и динамическим.

Статический стационарный режим (статика) – это режим, при котором система находится в состоянии покоя вследствие того, что все внешние воздействия и параметры самой системы не меняются во времени

Динамический стационарный режим возникает, когда приложенные к системе внешние воздействия изменяются по какому-либо установившемуся закону, в результате чего система приходит в режим установившегося вынужденного движения.

Статические характеристики определяют зависимость между выходной и входной величинами звена или системы в установившемся состоянии. Характеристики могут быть получены экспериментальным путем или же в результате аналитических или графо-аналитических расчетов. Знание характеристик звеньев и САУ необходимо для оценки их свойств, анализа и синтеза систем с требуемым качеством функционирования.

2.1. Статические звенья.Статическая характеристика типового звена САУ – это зависимость установившегося значения выходной величины X_уст. от установившегося значения входной величины y_уст.

X_уст. = f_ст. (y_уст.), (1)

где X_уст. – установившееся значение выходной величины; Y_уст. – установившееся значение входной величины; f - в общем случае произвольная нелинейная функция.

Звенья, имеющие такие зависимости, называются статическими.

Статическую характеристику линейного звена (системы), имеющего передаточную функцию 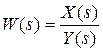, можно получить, используя теорему Лапласа о предельном значении оригинала

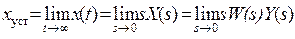, (2)

где W(0) – значение передаточной функции при s = 0, которое равно статическому коэффициенту передачи линейного звена (системы).

Для звена с линейной характеристикой зависимость (1) упрощается:

X_уст. = Кy_уст.. (3)

Если у звена несколько входных величин, то

X_уст. = f_n (y_уст.1, y_уст.2, …, y_уст.n). (4)

Если

X_уст. = f₂ (y_уст.1, y_уст.2.), (5)

то статическая характеристика геометрически становится поверхностью соответствующего измерения. Зависимость вида

X_уст. = f_а (y_уст., а), (6)

где а – параметр настройки, отображает семейство характеристик, каждая из которых соответствует своему значению а.

Статические характеристики могут быть выражены аналитической (1) - (6) или графической зависимостями. Статические характеристики систем (соединений) можно найти по известным статическим характеристикам образующих эти системы звеньев.

2.2.Последовательное соединение звеньев.Рассмотрим, например, определение статической характеристики последовательно соединенных трех звеньев – рисунок 1. Входная величина первого звена является входной величиной соединения (системы), выходная величина первого звена является входной величиной второго звена и т.д. Выходная величина последнего звена является выходной величиной соединения.

X уст.2 = y уст.3

X уст.1 = y уст.2

X уст.3 = X уст.

y уст. = y уст.1

W3(0)

W2(0)

W1(0)

Рисунок 1 – Последовательное соединение звеньев

Структурные преобразования соединения звеньев сохраняют силу для их статических пределов. Поэтому общий коэффициент для последовательного соединения звеньев равен

k = k₁k₂…k_m. (7)

2.3.Параллельное соединение звеньев.В этом случае входная величина соединения (системы) является одновременно входным сигналом для каждого звена – рисунок 2. Результирующая выходная величина соединения (системы) равна сумме выходных сигналов отдельных звеньев.

k = k₁ + k₂ +…+ k_m. (8)

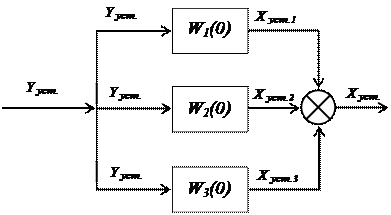
Рисунок 2 – Параллельное соединение звеньев

Последовательно-параллельное соединение звеньев.При таком соединении звеньев на вход звена одновременно с входной величиной подается ее выходная величина, преобразованная звеном обратной связи W_о.с.(s), как показано на рисунке 3.а.

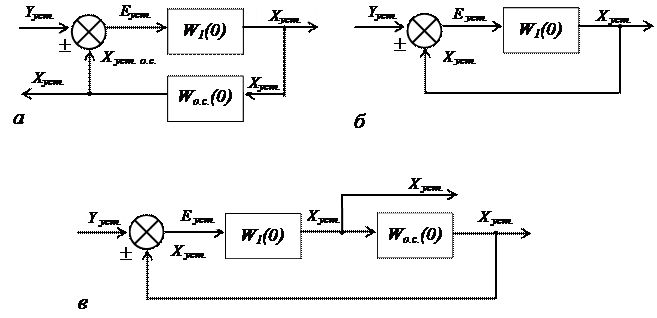
Рисунок 3 – Последовательно-параллельное соединение звеньев

a – параллельное расположение звеньев;

б – соединение с единичной обратной связью;

в – последовательное расположение звеньев

Как видно из схемы на вход звена в прямой цепи поступает разность между входной величиной соединения y_уст. и выходной величиной звена обратной связи x_{уст. о.с.}

e_уст. = y_уст. ± x_{уст. о.с.} (9) Для звена с усилением k₁,охваченного обратной связью с коэффициентом усиления k_о.с.

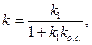(10)

При известной передаточной функции системы нет необходимости рассматривать статические пределы отдельных звеньев. Предельный коэффициент усиления k_р для разомкнутой системы определяют по формуле

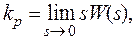(11)

а коэффициент усиления k_з для замкнутой системы

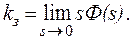(12)

В установившемся режиме структурная схема САУ остается прежней, однако звенья ее становятся динамически неразличимыми. Так, если передаточные функции трех звеньев: колебательного, апериодического и пропорционального имеют вид:

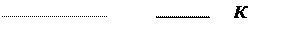К , К ,

T₁²s² +2T₂s +1 T₁s +1

то в установившемся режиме, когда оператор s ® 0, все звенья будут описываться только коэффициентом К. Приведенные формулы справедливы для систем без включенных последовательно интегрирующих звеньев.

Астатические и статические звенья.Не у всех звеньев имеется зависимость между установившимся значением выходной величины от установившегося значения входной величины. Примером может служить электродвигатель, если за его входную величину принять подводимое напряжение, а за выходную – угол поворота якоря. При подаче на электродвигатель напряжения угол поворота его якоря будет увеличиваться непрерывно с определенной скоростью. Такое звено статической характеристики не имеет. Такие звенья называются астатическими. У астатических звеньев при постоянном входном воздействии сигнал на выходе в установившемся режиме непрерывно растет с постоянной скоростью, ускорением и т.д. Для них существует другая статическая зависимость - между установившемся значением скорости выходной величины и установившемся значением входной величины

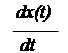= f_аст.(Y_уст.). (13)

Некоторые астатические звенья имеют постоянной не первую производную, а вторую, третью и т.д. В этом случае такие звенья обладают астатизмом второго, третьего и т.д. порядка. Признак того, что звено (или система в целом) является астатическим – это наличие комплексного переменного p в качестве сомножителя в знаменателе передаточной функции.

=

Если в передаточной функции звена (или системы)

W(s)=

Q(s) P(s)

bm sm +sb(m-1) s(m-1)+ …+ s1 p + b0 an sn + a(n-1) s(n-1) + …+ a1 s + a0

. (14)

коэффициенты а₀, а₁, …, а_(n-1) будут равны нулю, то передаточная функция примет вид:

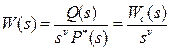, (15)

где

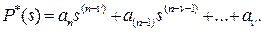(16)

Отсюда видно, что звено с передаточной функцией (15) можно представить в виде последовательного соединения n интегрирующих звеньев с передаточными функциями W_и(s)=1/s и звена с передаточной функцией ,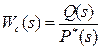

не содержащего последовательных интегрирующих и дифференцирующих элементов и имеющих коэффициент передачи k_c = b₀/a_n . Звенья с передаточной функцией вида W_c(s) являются статическими, так как при поступлении на их вход постоянной величины y_уст. установившееся значение выходной величины будет постоянным и равным

X_уст. = k_c y_уст. (17)

Это следует из того, что после поступления на вход звена с передаточной функцией W_c(s) постоянного воздействия по окончании переходного процесса все производные от выходной величины будут равны нулю. В статическом звене или системе величина W_c(0) равна передаточному коэффициенту

W_c(0) = k_c. (18)

kи s

Интегрирующее звено

W_и(s) = (19)

является астатическим, так как при поступлении на его вход постоянной величины y_уст. выходная величина будет беспрерывно возрастать

x = k_и y_уст.t (20)

с постоянной скоростью

dx/dt = k_и y_уст.. (21)

Таким образом, интегрирующее звено имеет постоянную первую производную от выходной величины при поступлении на его вход постоянного сигнала и, следовательно, обладает астатизмом первого порядка. Так как передаточная функция исходного звена (15) содержит n последовательно соединенных астатических звеньев первого порядка, то оно в целом является астатическим звеном n-го порядка. То есть, порядок астатизма по виду передаточной функции звена или соединения определяется степенью сомножителя p в ее знаменателе. Если за выходную величину такого звена принять производную dⁿx/dtⁿ = x⁽ⁿ⁾(t), то такое звено будет статическим, т.е.

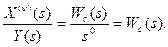(22)

В отношении же всех производных выходной величины более низких порядков это звено будет астатическим

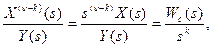(23)

где k = 1, 2, …, n - 1 – порядок астатизма, причем, чем ниже порядок производной выходной величины, тем выше порядок астатизма звена, если эту производную принимать за новую выходную величину.

В общем случае система астатизма n без установившейся ошибки отрабатывает задающие воздействия, описываемые в функции времени выражением

y(t) = 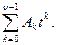(24)

Порядок выполнения работы

3.1.К выполнению лабораторной работы рекомендуется приступать только после внимательного ознакомления с теоретическим разделом настоящих методических указаний.

3.2. Письменно ответить на контрольные вопросы к лабораторной работе. Отчет с ответами (остается у студента) утвердить у преподавателя.

3.1. В исследуемой следящей системе (рис.1) по передаточным функциям элементов определить тип каждого динамического звена и построить его статическую характеристику по данным из таблицы 1.

3.2. Построить статическую характеристику системы в разомкнутом состоянии.

3.3. Построить статическую характеристику системы в замкнутом состоянии. Параметры корректирующего устройству взять из таблицы 2.

3.4. Оформить выполненную работу в виде отчета в соответствии с требованиями ГОСТа 2.105-95. Отчет выполнять на листах формата А4 (210х297 мм). Листы должны иметь штамп для текстовых документов (форма 2а, ГОСT 2.104-68).

3.5. Защитить выполненную работу у преподавателя и сдать отчет.

3.6. Все приведенные выше разделы лабораторной работы выполняются непосредственно в отведенное на лабораторную работу время (4 учебных часа).

Требования к содержанию отчета

Отчет по лабораторной работе должен содержать:

1. Ответы на контрольные вопросы к лабораторной работе.

2. Структурную схему исследуемой системы.

3. Исходные данные (с указанием варианта) для расчета, сведенные в таблицу.

4. Статические характеристики всех элементов системы (X_уст. = f(Y_уст.)).

5. Статическую характеристику системы в разомкнутом состоянии.

6. Статическую характеристику системы в замкнутом состоянии.

5. Контрольные вопросы

1. В каких режимах может работать САУ как динамическая система?

2. Дать определение статическому стационарному режиму работы.

3. Дать определение динамическому стационарному режиму работы.

4. Как определяют статические характеристики звена или системы?

5. Теорема Лапласа о предельном значении оригинала для получения статической характеристики линейного звена (системы).

6. Статическая характеристика звена с несколькими входными величинами?

7. Как графически определяется статическая характеристика соединения из нескольких последовательно соединенных звеньев?

8. Как графически определяется статическая характеристика соединения из нескольких параллельно соединенных звеньев?

9. Как графически определяется статическая характеристика соединения из нескольких последовательно-параллельно соединенных звеньев?

10. Дать определение астатическому звену (системе).

11. Что такое порядок астатизма звена (системы) и как он определяется?

Лабораторная работа № 2