Действующих начал природы восторг зрителя вызывает главным образом - Свет

Оглавление

· Введение.............................................................................................3 стр

· Показательные уравнения и их функции.....................................4-6 стр

· Способы решения показательных уравнений.............................7-9 стр

· Показательные неравенства........................................................10-11 стр

· Способы решения показательных неравенств.........................12-13 стр

· Логарифмические уравнения и их функции..............................14-16 стр

· Способы решение логарифмических уравнений.......................17-19 стр

· Логарифмические неравенства...................................................20 стр

· Способы решения логарифмических неравенств....................21-22 стр

· Примеры для самостоятельного решения..............................23-24 стр

· Используемая литература.........................................................25стр

.

Введение

“Из всех заслуживающих изучения первопричин и

Действующих начал природы восторг зрителя вызывает главным образом - Свет,

А из достопримечательностей Математики - разум

Исследователя в несравненно большей

Степени, чем всё остальное, возвышает

непреложность её доказательств.
Леонардо да Винчи

Название проекта: «Решение логарифмических и показательных уравнений и неравенств»

Краткая аннотация проекта:Проект предусматривает развитие самостоятельности при изучении темы: «Решение логарифмических и показательных уравнений и неравенств»и как это влияет на качественную подготовку.

Актуальность:

-Недостаток знаний у студентов о решении логарифмических и показательных уравнений и неравенств.

Цель проекта –формирование у каждого студента умения решать различные типы логарифмических и показательных уравнений и неравенств.

Задачи : обобщить и углубить знания студентов о показательных и логарифмических уравнениях и неравенствах.

Показательные уравнения и их функции

Функцию вида y= a^x, где a> 0 и a≠ 1, называют показательной функцией. Основные свойства показательной функции y= a^x:

График показательной функции

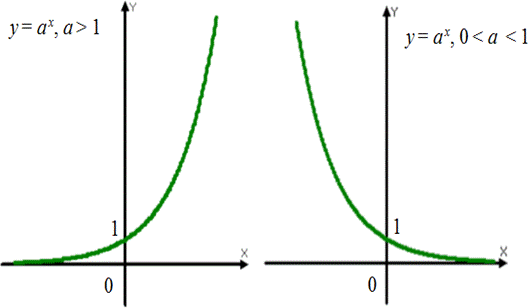
Свойства	a > 1	0 < a < 1
Область определения	D(f) = (-∞; +∞)	D(f) = (-∞; +∞)
Область значений	E(f) = (0; +∞)	E(f) = (0; +∞)
Монотонность	Возрастает	Убывает
Непрерывность	Непрерывная	Непрерывная

Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.

Теорема 1. Показательное уравнение af^(x) =ag^(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).

Основные формулы

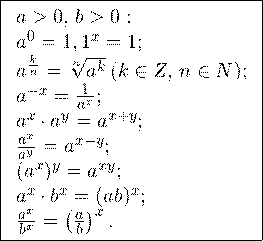
Пример 1. Решите уравнение:

2^2x+1-5•2^x-88=0

Решение: используем приведенные выше формулы и подстановку:

t=2^x

t > 0 !

Уравнение тогда принимает вид:

2t²-5t-88=0

Дискриминант полученного квадратного уравнения положителен:

D = b²-4ac = 5²- 4•2•(-88) = 729 = 27² > 0

Это означает, что данное уравнение имеет два корня. Находим их:

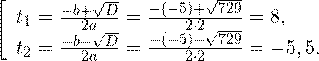
Переходя к обратной подстановке, получаем:

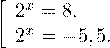
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем первое :

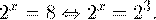
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.

Ответ: x = 3.

Способы решения показательных неравенств

Показательная функция в зависимости от основания может быть возрастающей (а>1) или убывающей (а<1)

Примеры.

Неравенства, сводящиеся к простейшим. Решаются приведением обеих частей неравенства к степени с одинаковым основанием.

а)2^x2> 2 ^x+2.

Решение:

2^x2> 2 ^x+2;
х² > х+2, т.к.функция y =2^t возрастает,
х² – х–2 > 0;
x < – 1; x > 2.

Ответ: .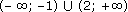

б) .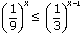

Решение:

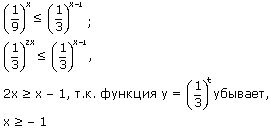
Ответ: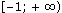

Неравенства, решаемые с помощью вынесения за скобки общего множителя.

8 × 2^{х – 1} – 2^х > 48

Решение: 2^х–1 (8 – 2) > 48,

2^х–1 > 8,

2^х–1 > 2³,

х – 1 > 3, т.к. функция y = 2^tвозрастает,

х > 4.

Ответ: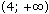

Неравенства, решаемые с помощью замены переменной.

2^х + 2^{3 – х} < 9

Решение:

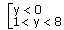
а) 2^х< 0. Неравенство решений не имеет, т.к. 2^х > 0.

б) 1 < 2^х< 8; 2⁰ < 2^х < 2³; 0 < x < 3, т.к. функция y = 2^х возрастает.

Ответ: (0; 3).

Свойства логарифмов

• Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:

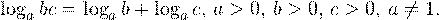
• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:

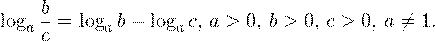
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:

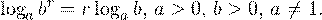
• Равенство log _a t = log _a s, где a > 0, a ≠ 1, t > 0, s > 0, справедливо тогда и только тогда, когда t = s.

• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):

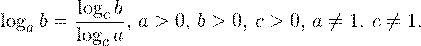
Теорема 1. Если f(x) > 0 и g(x) > 0, то логарифмическое уравнение log _a f(x) = log _a g(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).

Пример 1. Решите уравнение:

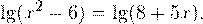
Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:

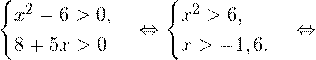
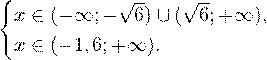
С учетом того, что

получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения:

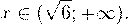
На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению:

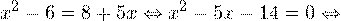
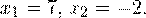
В область допустимых значений входит только первый корень.

Ответ: x = 7.

Пример 2. Решите уравнение:

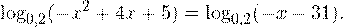
Решение. Область допустимых значений уравнения определяется системой неравенств:

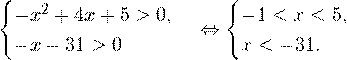
Эти два условия противоречат друг другу, то есть нет такого значения х ,при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет.

Ответ: корней нет.

Логарифмические неравенства

Логарифмическим неравенством называется неравенство, в котором неизвестная величина стоит под знаком логарифма.

Теорема 2. Если f(x) > 0 и g(x) > 0, то:
при a > 1 логарифмическое неравенство log _a f(x) > log _a g(x) равносильно неравенству того же смысла: f(x) > g(x);
при 0 < a < 1 логарифмическое неравенство log _a f(x) > log _a g(x) равносильно неравенству противоположного смысла: f(x) < g(x).

Пример 1. Решите неравенство:

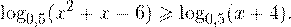
Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:

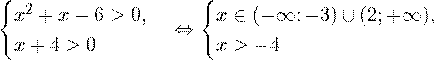
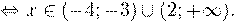
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству:

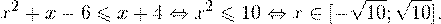
Окончательно, с учетом области допустимых значений получаем ответ:

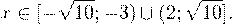
Оглавление

· Введение.............................................................................................3 стр

· Показательные уравнения и их функции.....................................4-6 стр

· Способы решения показательных уравнений.............................7-9 стр

· Показательные неравенства........................................................10-11 стр

· Способы решения показательных неравенств.........................12-13 стр

· Логарифмические уравнения и их функции..............................14-16 стр

· Способы решение логарифмических уравнений.......................17-19 стр

· Логарифмические неравенства...................................................20 стр

· Способы решения логарифмических неравенств....................21-22 стр

· Примеры для самостоятельного решения..............................23-24 стр

· Используемая литература.........................................................25стр

.

Введение

“Из всех заслуживающих изучения первопричин и

действующих начал природы восторг зрителя вызывает главным образом - Свет,