Проверка закона распределения по критерию согласия «хи-квадрат» Пирсона

Критерий согласия «хи-квадрат» Пирсона вычисляется по формуле (3.1):

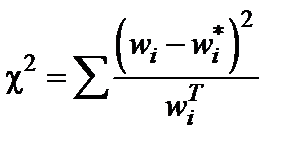, (3.1)

где, w_i – опытная частота;

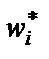– теоретическая частота;

i – номер интервала статистического ряда.

Суммирование производится по всем n интервалам. В первый столбец записываются номера интервалов, во второй переносятся из статистического ряда их верхние границы.

По ним вычисляются и записываются в третий столбец значения центрированного нормированного аргумента u для входа в таблицу интегральной функции ЗНР.

В следующий, четвертый столбец заносятся найденные по таблице значения интегральной функции для верхних границ интервалов.

В пятый столбец расчетной таблицы записываются значения теоретической вероятности р^* попадания случайной величины (в нашем примере – плунжера топливного насоса высокого давления (ТНВД)) в текущий интервал. Эта вероятность вычисляется как разность функции распределения по концам интервала, то есть как разность этой функции между текущим и предшествующим интервалами. Для первого интервала в этом столбце повторяется значение из четвертого столбца.

В шестой столбец переносятся из статистического ряда опытные частоты. Далее вычисляются и записываются в седьмой столбец теоретические частоты 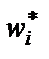как произведение объема выборки N на теоретическую вероятность 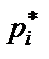.В восьмой столбец записываются квадраты разности опытных и теоретических частот.

В последний, девятый столбец расчетной таблицы записывается отношение квадрата разности частот к теоретической частоте. Сумма этого столбца и представляет собой искомый критерий «хи-квадрат».

Проследим на числовых примерах заполнение этой таблицы. Для первого интервала (первая строка таблицы) верхняя граница равна 14. Табличный аргумент для нее составит:

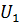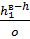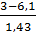= = =-2,167

В шестой столбец переносим из статистического ряда опытную частоту w₁ = 1. Далее находим и записываем в седьмой столбец теоретическую частоту w^*:

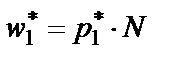= 0,0351·32 = 1,1232

В восьмой столбец записываем квадрат разности опытной и теоретической частот:

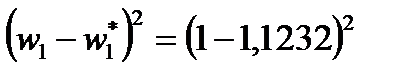= 0,0152.

В последний, девятый столбец записываем отношение квадрата разности частот к теоретической частоте:

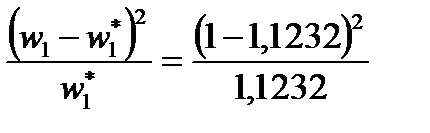≈ 0,0135.

По такой же методике выполняем расчет критерия «хи-квадрат» для ЗРВ износа плунжера топливного насоса высокого давления (ТНВД). Отличие заключается лишь в том, что величина u для распределения Вейбулла вычисляется по формуле (3.2), в то время как для ЗНР использовалась формула (3.3):

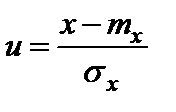, (3.2)

где u – табличный аргумент;

х – приведенное значение аргумента (значение случайной величины, для которой отыскивается вероятность или плотность).

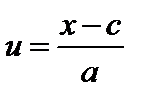, (3.3)

где с – параметр смещения ЗРВ;

а – масштабный параметр ЗРВ.

Другое существенное отличие заключается в следующем. Таблицы 1 и 2 (приложение 1) для ЗНР являются таблицами с одним входом, то есть они могут быть записаны в два столбца: столбец аргумента и столбец функции. В столбце аргумента находим нужное значение и в этой же строке считываем в столбце функции результат.

Таблицы 3 и 4 (приложение 1) для ЗРВ являются таблицами с двумя входами: кроме значения аргумента u (первый вход таблицы) необходимо также задавать значение параметра b (второй вход). Поэтому результат считывается из таблицы на пересечении строки с заданным значением u и столбца с заданным значением b. Естественно, если в точности заданных значений в таблице не содержится, приходится интерполировать по одному или по обоим входам таблицы. В этом случае следует использовать формулу (3.4):

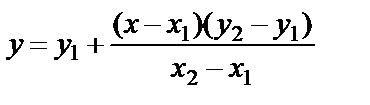, (3.4)

где х₁ и х₂ – ближайшие к заданному аргументу х табличные значения;

у₁ и у₂ – соответствующие табличные значения функции y.

Таблица 3.1

Расчет критерия «хи-квадрат» для ЗНР износа плунжера топливного насоса высокого давления (ТНВД)

Номер интервала	Верхняя граница интервала	Табличный аргумент	Интегральная функция	Теоретическая вероятность р*	Опытная частота	Теоретическая частота	Квадрат разности частот	Отношение
i		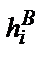		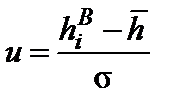	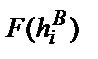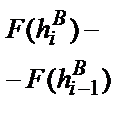wi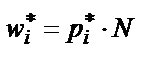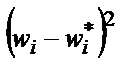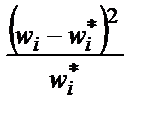
	3,5	–1,81	0,0351	0,035		1,123	0,015	0,013
	4,5	–1,11	0,1335	0,098		3,148	0,724	0,229
	5,5	–0,41	0,3409	0,207		6,636	2,679	0,403
	6,5	0,27	0,6064	0,265		8,496	0,254	0,029
	7,5	0,97	0,8340	0,227		7,283	1,646	0,225
	8,5	1,67	0,9525	0,118		3,792	10,29	2,713
							Сумма:	3,612

Итак, параметры ЗРВ для рассматриваемого примера (плунжера топливного насоса высокого давления (ТНВД)) составляют:

а = 4,05;

b = 2,35;

с = 2,5.

Таблица 3.2

Расчет критерия «хи-квадрат» для ЗРВ износа плунжера топливного насоса высокого давления (ТНВД)

Номер нтервала	Верхняя граница интервала	Табличный аргумент	Интегральная функция	Теоретическая вероятность р*	Опытная частота	Теоретическая частота	Квадрат разности частот	Отношение
i		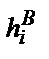		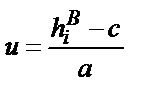	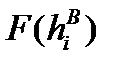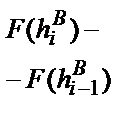wi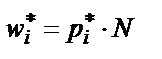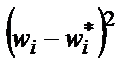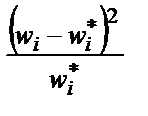
	3,5	0,24	0,024	0,024		0,768	0,053	0,069
	4,5	0,49	0,114	0,090		2,880	1,254	0,435
	5,5	0,74	0,356	0,242		7,744	7,529	0,972
	6,5	0,98	0,544	0,188		3,776	27,29	7,227
	7,5	1,23	0,781	0,237		7,584	2,509	0,330
	8,5	1,48	0,886	0,105		3,360	13,24	3,940
							Сумма:	12,973

Теперь можно сопоставить согласие опытных данных с ЗНР и с ЗРВ. Для этого находят число степеней свободы для каждого из рассматриваемых распределений по формуле (3.5)

k = n – s – 1, (3.5)

где k – число степеней свободы;

n – число интервалов статистического ряда;

s – число параметров закона распределения.

В нашем примере n = 6. Число параметров s для ЗНР равно 2 ( 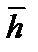и σ), для ЗРВ – 3 (a, b и c). Поэтому число степеней свободы равно:

для ЗНР – 6 – 2 – 1 = 3;

для ЗРВ – 6 – 3 – 1 = 2.

Определяем уровень значимости для ЗНР=0,31

для ЗРВ=0,01

Это позволяет без колебаний выбрать закон нормального распределения (ЗНР).