Определение числовых характеристик (статистик) опытного распределения вероятностей случайной величины

Определение числовых характеристик (статистик) опытного распределения вероятностей случайной величины

Последовательность обработки опытных данных

Каждое исследование случайных явлений, выполняемое методами теории вероятностей, как бы отвлеченно оно ни было, корнями своими всегда уходит в эксперимент, в опытные данные, в систему наблюдений.

Обработка опытных данных всегда ведется по какому-то одному количественному показателю: износу конкретной поверхности детали, наработке детали на отказ, ресурсу машины до капитального ремонта, затратам средств на обеспечение работоспособности машины данной марки в расчете на единицу наработки и т. п.

Методику обработки опытных данных рассмотрим на примерах математической обработки данных микрометражного обследования изношенных гильз цилиндров и поршневых пальцев двигателя Д260.2

Износ поверхности является случайной величиной, находящейся с той или иной вероятностью в границах некоторого поля рассеяния. Для его вероятностного (статистического) описания принимается следующий общий порядок действий:

1. Составить вариационный ряд величины износа.

2. На основе вариационного ряда сформировать статистический ряд износа.

3. Определить числовые характеристики распределения величины износа.

4. Проверить опытные данные на наличие выпадающих точек и при необходимости уточнить числовые характеристики распределения.

5. Построить графически гистограмму и полигон опытного распределения случайной величины.

6. Подобрать теоретический закон распределения случайной величины.

7. Освоить технику использования таблиц для нахождения функций и плотностей распределений: закона нормального распределения (ЗНР) и закона распределения Вейбулла (ЗРВ).

8. Проверить выбранный закон распределения по критерию согласия «хи-квадрат» Пирсона.

9. Определить доверительные границы рассеивания среднего значения случайной величины.

10. Определить относительную ошибку расчета характеристик случайной величины и проверить достаточность объема выборки.

11. Рассчитать значения и построить график дифференциальной и интегральной функций выбранных теоретических распределений.

При обследовании плунжера замерялся максимальный радиальный износ плунжера топливного насоса высокого давления (ТНВД) в зоне работы верхнего компрессионного кольца вблизи ВМТ.

Замер износа плунжера по диаметру производился в средней части пальца: в зоне сопряжения с втулкой верхней головки шатуна. Данные микрометража приведены в табл. 1.1

Таблица 1.1

Данные микрометража, мм

Износы плунжера топливного насоса высокого давления (ТНВД)
0,04	0,06	0,07	0,08	0,06	0,06	0,06	0,07
0,07	0,06	0,06	0,08	0,03	0,07	0,08	0,07
0,04	0,04	0,05	0,09	0,05	0,04	0,05	0,07
0,05	0,08	0,06	0,06	0,08	0,05	0,09	0,06

Для упрощения дальнейших вычислений целесообразно преобразовать десятичные дроби в целые числа. Этого можно добиться, если каждое из значений исходной информации умножить на 100.

Например, 0,19 мм × 100 = 19 и читается так: радиальный износ плунжера топливного насоса высокого давления (ТНВД) составляет 19 сотых долей миллиметра. В случае, если замеры износа возможны до третьего знака после

запятой (с микронной точностью), например 0,197, то это число, для превращения его в целое, нужно умножить на 1000, т.е. 0,197 × 1000 = 197 и читается так: радиальный износ гильзы составляет 197 тысячных долей миллиметра, или 197 мкм

Переход к приведенным числам измерения исследуемого параметра осуществляется путем умножения натурального значения этого параметра на 10ⁿ, где n – любое целое число, кроме 0.

Вариационный ряд

Вариационный ряд – это упорядоченный по возрастанию исходный ряд значений исследуемого признака.

По принятой в статистике терминологии отдельная компонента (член, элемент) вариационного ряда называется вариантой. Количество вариант вариационного ряда всегда равно объему выборки N.

Таблица 1.2

Вариационный ряд

Износы плунжера топливного насоса высокого давления (ТНВД)

Используя вариационные ряды, определяем следующие величины, которые потребуются для формирования статистических рядов:

h_min – минимальное значение износа (первая варианта);

h_max – максимальное значение износа (последняя варианта);

R = h_max – h_min – размах выборки;

N – объем выборки (количество членов вариационного ряда).

Для износа плунжера топливного насоса высокого давления (ТНВД) составят:

h_min = 3, h_max = 9, R = 9–3 = 9, N =32;

Статистический ряд

Статистический ряд составляется в виде табл.1.3, состоящей из семи столбцов: номер интервала i, нижняя граница интервала h^н, верхняя граница интервала h^в, середина интервала h^с, частота w, опытная вероятность (частость) р и накопленная опытная вероятность Р.

Число строк таблицы равно количеству интервалов статистического ряда, которое, в свою очередь, зависит от объема выборки N. Эта зависимость выражается формулой

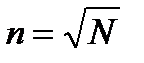, (1.1)

где n – количество интервалов;

N – объем выборки.

Полученный результат округляют в сторону увеличения до ближайшего целого числа. Количество интервалов не должно выходить за пределы n = 6…20.

Поскольку объем выборки в обоих рассматриваемых примерах одинаков, одинаковыми будут и числа интервалов для обоих статистических рядов:

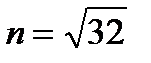= 5,66 ≈ 6.

Желательно, чтобы все интервалы статистического ряда были равны по величине и не имели разрывов. Величину А одного интервала определяют по уравнению:

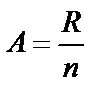(1.2)

где А – величина интервала в измерения единицах случайной величины;

R – размах выборки в тех же единицах;

n – количество интервалов статистического ряда.

Значение величины интервала, полученное по формуле (1.2), всегда округляют в большую сторону до величины, удобной для дальнейших расчетов.

Для износов плунжера топливного насоса высокого давления (ТНВД)

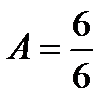= 1

Далее определяют нижние и верхние границы интервалов и середины интервалов. В качестве нижней границы первого интервала принимается начало поля рассеяния:

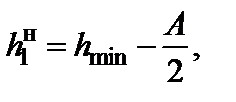(1.3)

где 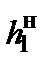– нижняя граница первого интервала;

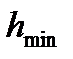– минимальное значение износа;

А – величина интервала.

Для износов плунжера топливного насоса высокого давления (ТНВД)

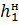= 3- =2,5

В случае если нижняя граница первого интервала получается отрицательной, она принимается равной нулю.

Для каждого из последующих интервалов нижняя граница текущего интервала определяется, как сумма нижней границы предыдущего интервала и величины интервала [3]:

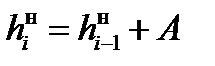(1.4)

Верхняя граница для любого интервала определяется, как сумма нижней его границы и величины интервала:

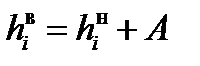=2,5+1=3,5 (1.5)

Середина интервала определяется как полусумма его нижней и верхней границ:

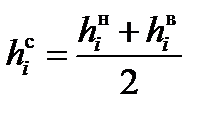(1.6)

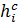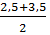= = 3

После заполнения первых четырех столбцов табл.1.3 статистического ряда можно найти частоту w_i для каждого интервала. Для этого следует произвести разноску всех вариант вариационного ряда по интервалам

статистического ряда, то есть для каждой варианты h_j (j = 1, 2, 3, …, N) определить номер интервала i (i = 1, 2, 3, …, n), которому она принадлежит, а для каждого интервала – число вариант, попадающих в данный интервал (частоту).

Частотой называется число вариант, попавших в данный интервал (именно число вариант, а не сумма их значений). Для первого интервала статистического ряда износов гильз частота w₁ равна 5, поскольку в этот интервал попадают первые пять вариант вариационного ряда. Следующие девять вариант (с шестой по четырнадцатую включительно) попадают во второй интервал, поэтому для него частота w₂ = 9.

В третий интервал попадают варианты с пятнадцатой по двадцать вторую включительно (всего восемь), поэтому w₃ = 8. Аналогичным образом находим частоты для остальных интервалов: w₄ = 5, w₅ = 3 и w₆ = 2.

Опытной вероятностью (или частостью) р_i в статистике принято называть отношение частоты w_i к объему выборки N:

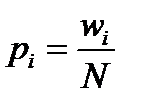(1.7)

В первом интервале

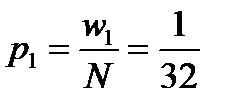=0,03125,

во втором интервале опытная вероятность

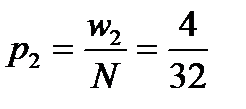= 0,125 и так далее.

В последний столбец статистического ряда записывается накопленная опытная вероятность Р_i, вычисляемая по формуле [3]:

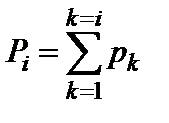. (1.8)

Таблица 1.3

Статистический ряд износов плунжера топливного насоса высокого давления (ТНВД)

Номер интервала	Нижняя граница интервала	Верхняя граница интервала	Середина интервала	Частота	Опытная вероятность (частость)	Накопленная опытная вероятность
i		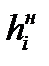		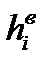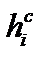wi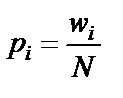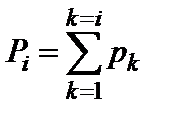
	2,5	3,5			0,031	0,031
	3,5	4,5			0,125	0,156
	4,5	5,5			0,156	0,312
	5,5	6,5			0,281	0,593
	6,5	7,5			0,187	0,78
	7,5	8,5			0,218	0,99

Закон распределения Вейбулла (ЗРВ)

Формулы дифференциальной и интегральной функций для ЗРВ имеют вид:

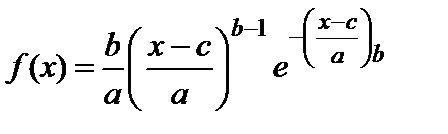, (2.4)

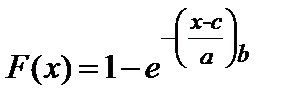, (2.5)

где а – масштабный параметр;

b – параметр формы;

с – параметр смещения (сдвига).

Следует найти вспомогательную величину V_c по формуле (2.6)

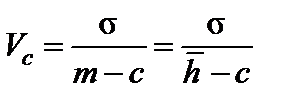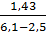= = 0,397 (2.6)

где σ – среднеквадратическое отклонение;

m – математическое ожидание ( );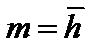

с – параметр смещения.

Находим параметр b и коэффициент К_а:

– для износов плунжера топливного насоса высокого давления (ТНВД)

b = 2,696;

К_а = 1,125;

Далее с использованием найденного коэффициента К_а находим параметр а по формуле:

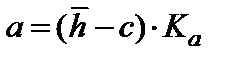. (2.7)

Для износов плунжера топливного насоса высокого давления (ТНВД)

а = (6,1-2,5)·1,125 = 4,05;

Метод разделяющих разбиений

Один из не очень точных, но зато наименее трудоемких методов нахождения оценок для параметров распределения – метод разделяющих разбиений – подробно описан в ряде источников.

Рассмотрим технику его применения на числовом примере. Требуется найти оценки параметров распределения Вейбулла с порогом чувствительности (трехпараметрическое распределение Вейбулла). Интегральная функция распределения для этого закона выражается формулой [3]:

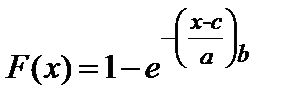, (2.8)

где х – радиальный износ гильзы, мм/100;

а – масштабный параметр;

b – параметр формы;

с – параметр смещения.

Параметр смещения с принимаем равным началу поля рассеяния, то есть, нижней границе первого интервала статистического ряда:

с = 2,5 мм/100.

Таблица 1.2.1

Радиальный износ плунжера топливного насоса высокого давления (ТНВД), мм/100

Номер интервала	Верхняя граница	То же, смещенная	Накопленная опытная вероятность
i	х	х–с	Рнакопл
	3,5		0,031
	4,5		0,156
	5,5		0,312
	6,5		0,593
	7,5		0,78
	8,5		0,99

Далее выполняем следующие шаги:

Шаг 1. Выбираем произвольно два интервала i₁ и i₂ статистического ряда. Интервалы желательно выбирать ближе к началу и концу статистического ряда, причем, i₁ < i₂. Выберем i₁ = 2 и i₂ = 5. Из соответствующих строк третьего столбца таблицы выписываем значения х₁ = 2 и х₂ = 5.

Шаг 2. Из соответствующих строк четвертого столбца таблицы выписываем значения накопленных опытных вероятностей Р₁ = 0,156 и Р₂ = 0,78.

Шаг 3. Находим параметр b по формуле [3]:

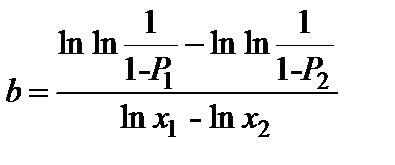. (2.9)

Подставляя выбранные нами значения х₁, х₂, Р₁ и Р₂, получаем:

b =2,35

Шаг 4. Находим параметр а:

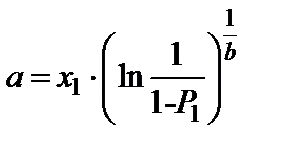(2.10)

После подстановки значений х₁ и Р₁ получаем:

а = 0,94

Искомые оценки параметров распределения ЗРВ составляют:

а = 0,94;

b = 2,35;

с = 2,5;

Для облегчения вычисления значений логарифмов и двойных логарифмов входящей в формулы (2.9) и (2.10) дроби 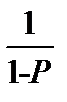приведены их значения при изменении Р в диапазоне 0,01–0,99.

Графический метод

У подавляющего большинства законов распределения график интегральной функции представляет собой кривую. Основная идея графических методов состоит в том, чтобы «выпрямить» эту кривую, то есть, подобрать для осей координат такие переменные масштабы, которые превратили бы график функции распределения в прямую линию.

В случае экспоненциального распределения это достигается созданием логарифмической шкалы на оси ординат. Для распределения Вейбулла логарифмическими шкалами снабжают и ось ординат, и ость абсцисс.

Если график снабдить соответствующими линиями сетки для обеих осей, то это позволяет легко наносить на график экспериментальные точки. Через эти точки на глаз проводится прямая, которая проходила бы как можно ближе ко всем точкам. Эта прямая и будет графиком интегральной функции в принятой системе координат.

Для нахождения параметров функции в этом случае легко применить простые приближенные методы обработки эмпирических зависимостей, такие, как метод выбранных точек, метод натянутых нитей и др. [6].

В практике обработки опытных данных при изучении случайных величин широко используется построенная по описанному принципу вероятностная бумага. Опишем технику использования вероятностной бумаги для оценки параметров распределения Вейбулла. Пусть требуется с использованием вероятностной бумаги найти оценки параметров ранее рассмотренного распределения Вейбулла для износа [3].

Вероятностная бумага для распределения Вейбулла (рис.2.4) представляет собой логарифмическую сетку. Для расширения диапазона варьирования случайной величины х подразумевается, что по оси абсцисс откладывается ее масштабированное значение, то есть произведение х·10^j, где j – целое число (порядок масштабного множителя).

В рассматриваемом примере величина х изменяется в пределах 2–12 (третий столбец табл. 1.3.3), поэтому j целесообразно принять равным нулю. Если бы износ замерялся не в сотых долях миллиметра, а в миллиметрах, то величина х варьировала бы в диапазоне 0,02–0,12. В этом случае j следовало бы принять равным 2. Аналогично, если бы х варьировала в диапазоне 20–120 единиц, то j следовало бы принять равным –1.

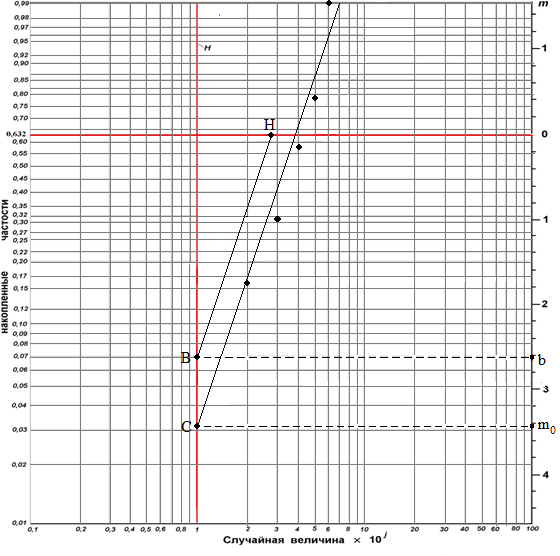
Рисунок 2.4 - Вероятностная бумага распределения Вейбулла

Таким образом, при j = 0 шкала оси абсцисс позволяет поместить величину в интервале 0,1–100, при j = 1 – в интервале 1–1000, при j = =2 – в интервале 10–10000 и т. д. Величина j может принимать и отрицательные значения. Например, при j = –1 диапазон шкалы оси абсцисс составит 0,01–10, при j = –2 – 0,001–1 и т. д.

Помимо сетки, вероятностная бумага для распределения Вейбулла снабжена двумя вспомогательными линиями и вспомогательной шкалой m, расположенной вертикально в правой части листа.

Первая вспомогательная линия (на рисунке обозначена буквой Н) является вертикалью с абсциссой, равной 1. Вторая вспомогательная линия – горизонталь с ординатой 0,632.

На этой линии отмечена точка А с абсциссой 2,718 (основание натуральных логарифмов). Эта линия определяет также нулевое значение шкалы m. Для нахождения параметров распределения следует отложить на сетке все экспериментальные точки статистического ряда, используя в качестве абсциссы третий столбец таблицы, а в качестве ординаты – четвертый (накопленные опытные вероятности). Через отложенные точки на глаз проводится прямая, проходящая на минимальном расстоянии от всех точек. Эта прямая представляет собой график интегральной функции распределения.

Для нахождения параметра b из точки А проводится прямая, параллельная функции распределения. Из точки В пересечения этой прямой со вспомогательной прямой Н проводится горизонталь до пересечения со шкалой m и по этой горизонтали со шкалы m считывается значение параметра b. В данном случае оно равно ≈ 1,73.

Точка С пересечения функции распределения со вспомогательной прямой Н используется для определения параметра а. Для этого из точки С проводят до шкалы m горизонталь и считывают на шкале m вспомогательную величину m₀. В нашем примере она получилась равной ≈ 2,93.

Параметр а находится по формуле (2.11):

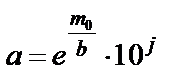, (2.11)

где m₀ – вспомогательная величина, считанная по шкале m;

b – параметр формы обрабатываемого распределения Вейбулла;

j – порядок масштабного множителя.

Подставляя в эту формулу значения из нашего примера m₀ = 3,4, b = 2,6, и j = 0, получаем

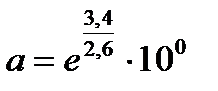= 3,7

Таким образом, найденные с использованием вероятностной бумаги параметры распределения составляют:

а = 3,7;

b = 2,6;

с = 2,5.

Как видим, совпадение с результатами применения метода разделяющих разбиений весьма хорошее. Однако, следует иметь в виду, что точность метода разделяющих разбиений существенно ниже, поскольку он из всей совокупности опытных данных использует всего лишь две экспериментальных точки. Поэтому использование вероятностной бумаги всегда предпочтительнее, хотя несколько более трудоемко.

Определение числовых характеристик (статистик) опытного распределения вероятностей случайной величины