Закон распределения дискретной случайной величины

Напомним, что дискретная случайная величина прини­мает отдельные изолированные значения.

Законом распределения дискретной случайной вели­чины x называется таблица

,

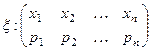где x₁ < x₂ < … < x_n – возможные значений величины x,

а p_k (k = 1, …, n) – их вероятности, то есть р_k = P(x =х_к ).

При этом должно выполняться равенство р₁ + р₂ + … + р_n = 1.

Это равенство означает, что при испытании одно из значений заведомо реализуется. Таблица показывает, как суммарная вероятность 100% распределяется по возможным значениям случайной величины. отсюда термин "закон распределения".

Пример. Производятся три выстрела по цели. Вероят­ность попадания при одном выстреле равна 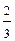. Найти закон распределения числа попаданий в цель.

Решение. имеем схему Бернулли, где успехом является попадание в цель 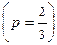, число испытаний n = 3, x – число успехов после трех испытаний. Требуется найти закон распределения случайной величины x.

Пользуясь формулой Бернулли ,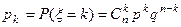

найдем

,

,

,

.

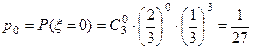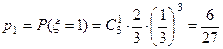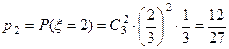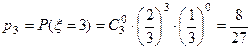Итого .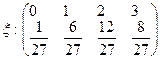

Математическое ожидание дискретной случайной величины

При решении инженерных задач, связанных с расчетом случая, фундаментальную роль играют так называемые числовые характеристики случайных величин: математическое ожидание и дисперсия. математическое ожидание имеет смысл центрального значения случайной величины. дисперсия характеризует разброс значений случайной величины относительно центра. В этом и следующем параграфах мы изучим эти понятия для дискретной случайной величины.

Пусть x - дискретная случайная величина с законом распределения

.

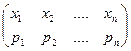Математическим ожиданием случайной величины x называется число:

М [ x ] = m_x = x₁· p₁ + x₂ · p₂ + … + x_n · p_n

(сумма произведений возможных значений на их вероятно­сти).

Пример 1.

.

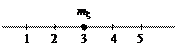
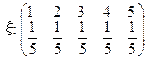
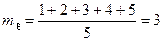мы видим: если значения x равновозможны, то математическое ожидание совпадает со средним арифметическим возможных значений x.

Пример 2.

.

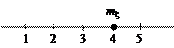
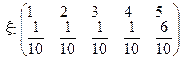
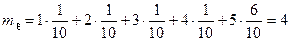Помнить: математическое ожидание характеризует центральное значение случайной величины с учетом возможных значений и их вероятностей: маловероятные значения вносят малый вклад в формирование математического ожидания, наиболее вероятные значения вносят основной вклад.

Свойства математического ожидания.

1⁰. М [ a ] = а.

Математическое ожидание неслучайной величины равно самой величине.

2⁰. М [ а x ] = a M [ x ].

Неслучайный множитель выносится за знак математиче­ского ожидания.

3⁰. M [ x + h ] = M [ x ] + M [ h ].

Математическое ожидание суммы случайных величин равно сумме математических ожиданий.

4⁰. Если x, h статистически независимы, то

M [ x · h ] = M [ x ] · M [ h ].

Доказательство.

1. Имеем: 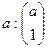, откуда получаем m_a = 1· a = a.

2. Пусть

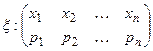, тогда ,

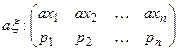откуда М [ а x ] = ax₁· p₁ + ax₂· p₂ +…+ ax_n· p_n = a M [ x ].

Для наглядности далее будем предполагать, что x, h при­ни­мают два возможных значения:

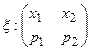; h .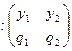

3. x + h : ;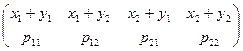

M [ x + h ] ;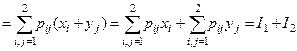

I₁ = p₁₁ x₁ + p₁₂ x₁ + p₂₁ x₂ + p₂₂ x₂ = (p₁₁ + p₁₂)x₁ + (p₂₁ + p₂₂)x₂.

;

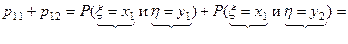
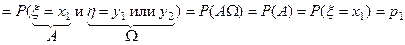доказано: р₁₁ + р₁₂ = р₁­, аналогично получим: р₂₁ + р₂₂ = р₂,

тем самым I₁ = p₁x₁ + p₂x₂ = M [ x ].

Также доказывается, что I₂ = M [ h ].

4. В силу теоремы умножения для независимых событий имеем: x · h : .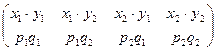

Тогда

M [ x · h ] = p₁q₁x_1­y₁ + p₁q₂x_1­y₂ + p₂q₁x_2­y₁ + p₂q₂x_2­y₂ =

= (p₁x₁ + p₂x₂) · (q₁y₁ + q₂y₂) = M [ x ] · M [ h ].