Модель обратной связи – использование теории оптимального

планирования эксперимента

Для сокращения числа имитационных экспериментов (расчетов на ЭВМ) при сохранении заданной точности в последнее время находят все более широкое применение методы теории оптимального планирования эксперимента. Планирование эксперимента в задачах моделирования состоит в выборе логической структуры искусственного эксперимента на ЭВМ и позволяет обоснованно проводить выбор значений управляемых параметров для выполнения расчетов на модели.

В планировании экспериментов для описания результирующей характеристики (в нашем случае – критерия оптимальности) используют полиномиальные модели, аппроксимирующие реальный вид целевой функции:

.

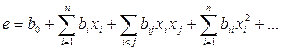Эта функция в планировании экспериментов называется функцией отклика или уравнением регрессии, пространство, в котором строится функция отклика, – факторным пространством (рис. 4.6.).

Коэффициенты функции отклика 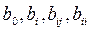и т.п. можно интерпретировать как значения частных производных в точке, вокруг которой производится разложение в ряд неизвестной целевой функции.

Для поиска оптимума в области определения факторов 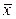выбирают произвольную точку А₁.

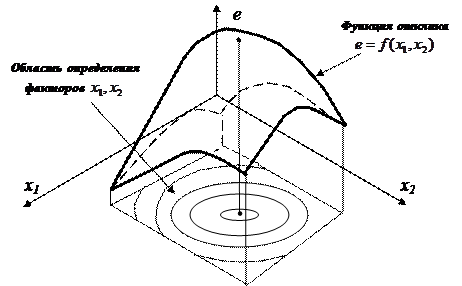
Рис. 4.6. Функция отклика и факторное пространство

В окрестности точки А₁ выделяют малую подобласть, в которой возможно описать функцию отклика полиномом первой степени (рис. 4.7). В этой подобласти осуществляют небольшую серию экспериментов (точки I), необходимую для построения линейной модели:

.

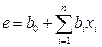Коэффициенты регрессии b_i используются для определения направления градиента, следуя которому осуществляют дальнейшие опыты (точки II в окрестности точки А₂). Для каждой новой подобласти вновь определяют направление градиента, по которому следуют в дальнейших опытах до тех пор, пока не достигнут оптимума – область М.

Рис. 4.7. Планирование имитационных экспериментов при

оптимизации по градиенту

Значения коэффициентов регрессии определяют по формуле

,

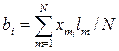где 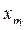– значение i-го фактора в m-м эксперименте; l_m – значение выходной характеристики в m-м эксперименте; n – общее число экспериментов в подобласти.

Информацию для проведения эксперимента записывают в матрице планирования эксперимента (табл. 4.1),называемой планом эксперимента.

Таблица 4.1. Матрица планирования эксперимента

№ опыта	Значения факторов	Значение результата
x1	…	xi	…	xn
	x11	…	x1i	…	x1n	l1
…	…	…	…	…	…	…
m	xm1	…	xmi	…	xmn	lm
…	…	…	…	…	…	…
N	xN1	…	xNi	…	xNn	lN

Для получения коэффициентов регрессии b_i с высокой точностью и достоверностью к плану эксперимента предъявляется ряд требований, что приводит к формированию значений 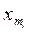по специальным правилам.

Процедура выбора подобласти проведения эксперимента состоит из двух этапов: выбор основного уровня 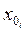и выбор интервалов варьирования I_i. Основной уровень – центр подобласти проведения эксперимента – для первого эксперимента осуществляется эвристически на базе анализа априорной информации. В дальнейшем его величина определяется направлением градиента и шагом эксперимента.

Интервалом варьирования I_i фактора x_i называется некоторое число, прибавление которого к основному уровню дает верхний 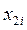, вычитание – нижний уровень фактора .

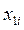Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по кодированным осям 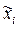и начало отсчета выбирают так, чтобы верхний уровень соответствовал +1, нижний –1, а основной – 0:

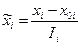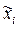, – кодированное значение фактора.

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом. Так как число уровней каждого фактора равно двум, то в теории планирования экспериментов рассматривается полный факторный эксперимент n². Для двух факторов план эксперимента и геометрическая интерпретация матрицы планирования 2² приведены на рис. 4.8..

Полный факторный эксперимент 2² будет иметь восемь опытов, а его геометрическая интерпретация представляет собой куб

Матрица полного факторного эксперимента строится следующим образом: в первои столбце знаки меняются поочередно, во втором – через два, в третьем – через четыре и т.д. по степени двойки. Однако полный факторный эксперимент содержит избыточную информацию для определения коэффициентов регрессии b_i, для расчета которых достаточно провести часть полного факторного эксперимента – дробный факторный эксперимент.

Реализуемая часть полного факторного эксперимента называется дробной репликой. Объем дробного факторного эксперимента определяется из следующих условий:

число экспериментов должно быть не меньше числа неизвестных коэффициентов в уравнении регрессии;

число экспериментов должно быть обязательно равно степени числа 2.

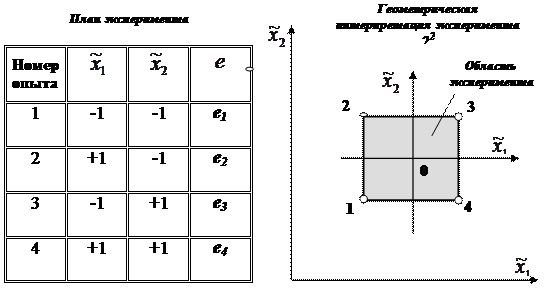
Рис. 4.8. План и графическая интерпретация эксперимента 2²

Так, для определения 11 коэффициентов уравнения линейной регрессии с 10 факторами требуется провести не менее 11 экспериментов. Ближайшее число по степени 2 – это число 16. Оно и определяет объем дробного факторного эксперимента. Так как 18 = 2⁴, а объем полного факторного эксперимента 2^11-7 в силу того, что 2^11-7 = 2⁴ = 16.

Как видно из таблицы 4.2. применение дробного факторного эксперимента для случая 15 факторов уменьшается объем расчетов по определению направления градиента в 2048 раз по сравнению с полным факторным экспериментом.

Таблица 4.2. Дробные реплики

Количество факторов	Дробная реплика	Условное обозначение	Количество опытов с дробной репликой	Количество опытов полного эксперимента
	1/2 реплики от 23	23-1
	1/2 реплики от 24	24-1
	1/4 реплики от 25	25-2
	1/4 реплики от 26	26-3
	1/16 реплики от 27	27-4
	1/64 реплики от 210	210-6
	1/2048 реплики от 215	215-11

Увеличение числа факторов в еще большей степени способствует повышению вычислительной эффективности этого метода.

Естественно. Что далеко не любые эксперименты из плана полного факторного эксперимента могут быть использованы при формировании плана дробного факторного эксперимента. Совокупность экспериментов в дробной реплике должна удовлетворять следующим свойствам:

1. Симметричность относительно центра эксперимента – алгебраическая сумма экспериментов-столбцов каждого фактора должна быть равна нулю, кроме столбца, отвечающего свободному члену b₀, т.е

,

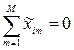где m –номер точки опыта; i– номер фактора; M –число различных точек плана матрицы дробной реплики.

2. Нормировка – сумма квадратов элементов каждого столбца равна числу точек матрицы, т.е.

.

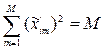3. Ортогональность – сумма построчных произведений плана матрицы любых двух столбцов равна нулю, т.е.

,

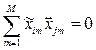где j – комбинация факторов в m-й точке .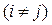

Ортогональность матрицы позволяет оценить все коэффициенты регрессии независимо друг от друга, т.е. значение любого коэффициента не зависит от того, какие значения имеют другие коэффициенты.

Если план дробной реплики отвечает указанным свойствам, то математическая модель, полученная в результате эксперимента, способна предсказать значения искомого показателя е с одинаковой точностью в любых направлениях на равных расстояниях от центра эксперимента или плана матрицы (свойство рототабельности).

После обработки данных эксперимента и вычисления коэффициентов регрессии b_i определяют следующие значения основного уровня по всем факторам . В основу алгоритма определения улучшенных значений основного уровня могут быть положены симплекс-метод, градиентный и др. Например, для движения по градиенту методом Бокса-Вильсона рекомендуется (см. рис. 4.7):

1) рассчитать составляющие градиента ;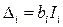

2) подобрать масштаб для шага изменения основного уровня k;

3) определить новые значения основных уровней по формуле

;

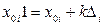4) рассчитать значения целевой функции для точки с координатами 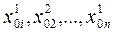и сравнить его с наилучшим значением из предыдущей серии экспериментов;

5) если шаг выбран удачно, т.е. получено улучшение, продолжать увеличивать значение основных уровней факторов на величину 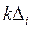; если произошло ухудшение, то следует уменьшить масштаб;

6) значение точки, в которой достигнуто максимальное улучшение значения целевой функции, принять за центр новой подобласти проведения эксперимента; относительно этой точки вновь повторить вышеописанную процедуру и искать направление градиента.

7) Если значения коэффициентов регрессии b_i близки к нулю, то это означает, что недалеко находится область оптимума. Для отыскания оптимального решения в этом случае необходимо переходить на полиномиальные уравнения более высокого порядка, например, использовать полином второй степени.