Методы многокритериальной оптимизации

Эффективность функционирования производственных объектов любой сложности количественно оценивается соответствующими системами технико-экономических показателей. При этом очевидно, что оптимальное значение одного или нескольких показателей не означает, что данное состояние объекта наилучшее, так как значения остальных показателей для него могут быть ниже, чем для других состояний.

В этих условиях возникает задача нахождения такого состояния (например, варианта плана производства продукции), в котором значения всех рассматриваемых показателей были бы пусть и не оптимальными, но в определенном смысле наилучшими по выполнению всех показателей одновременно. Такие планы называют компромиссно-оптимальными, а задачи их поиска – принятием сложного решения.

Наиболее общая математическая формулировка многокритериальных задач принятия решений представлена выражениями (2.12), (2.13) к общей формулировке многокритериальной задачи принятия решения могут сводиться задачи различного происхождения, которые можно классифицировать на четыре типа:

1. Задачи оптимизации на множестве целей. Имеется множество разнородных целей, каждая из которых должна быть учтена при выборе оптимального решения.

2. Задачи оптимизации на множестве объектов. Рассматривается совокупность объектов, качество функционирования каждого из которых оценивается самостоятельным критерием; качество функционирования совокупности объектов оценивается векторным критерием, составленным из частных критериев, характеризующих каждый объект.

3. Задачи оптимизации на множестве условий функционирования – задан спектр условий, в которых предстоит работать объекту, и применительно к каждому условию качество функционирования оценивается некоторым частным критерием.

4. Задачи оптимизации на множестве этапов функционирования – рассматривается функционирование объекта на некотором интервале времени, разбитом на несколько этапов; качество управления на каждом этапе оценивается частным критерием, а на множестве этапов – общим векторным критерием.

В задачах 2, 3, 4-го типа частные критерии имеют обычно единую размерность.

Для случая, описываемого выражениями (2.12), (2.13), вид платежной матрицы (см таблицу 3.2) остается прежним. Платежные матрицы соответствующие каждому частному критерию, будут образовывать макростолбцы общей платежной матрицы исследуемой ситуации. Для случая детерминированной задачи вся информация для принятия решения также будет соответствовать определенному критерию, а не набору значений неопределенных факторов.

Наиболее сложным для практики является решение задач первого типа, для которых множество критериев оптимальности в принципе не имеет единой размерности. Для возможности сравнения частных решений необходимо приведение частных критериев к одинаковой размерности. Наиболее распространенным способом решения этой проблемы является нормировка критериев – приведение их к безразмерному виду по формулам

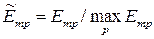
для критериев, которые стремятся увеличивать, и

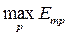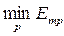для критериев, которые стремятся уменьшить. При этом и означают соответственно максимальное или минимальное значение p-го критерия оптимальности.

Таким образом, после нормировки вместо матрицы 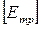, в который элементы столбцов имели различную размерность, получается матрица 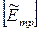, размерность элементов которой от 0 до 1: .

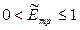К полученной матрице 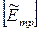в принципе можно применять критерии, приведенные выше. Однако в ситуации принятия решений по многим критериям исследователь зачастую обладает дополнительной информацией о важности того или иного критерия оптимальности. Эта эвристическая информация с помощью методов экспертной оценки может формироваться в виде коэффициентов важности каждого p-го критерия – .

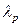В литературе описываются всевозможные принципы оптимальности и соответствующие им схемы компромисса между решениями, получаемыми по частным критериям. Сюда относятся принцип равенства, квазиравенства, равномерности, справедливой абсолютной и относительной уступки, последовательной уступки, выделения главного критерия и ряд других. До недавнего времени наиболее часто использовались следующие показатели свертки нескольких критериев оптимальности в единую целевую функцию:

критерий справедливости абсолютной уступки

;

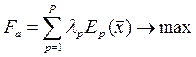критерий справедливой относительной уступки

,

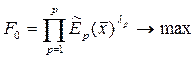где 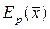– нормированное значение p-го критерия оптимальности 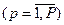; λ_p – коэффициент важности свертки p-го критерия.

Однако, как показала практика, в большинстве случаев оптимальное решение достаточно чувствительно к изменению коэффициентов важности λ_p. Получение этих коэффициентов экспертными методами дает достаточно большую величину доверительного интервала для их средних значений. Однако даже незначительная область изменения значений коэффициентов важности приводит к появлению множества решений, оптимальных для этой области, – к «размыванию» оптимального решения.

Именно поэтому в последнее время большое распространение среди методов многокритериальной оптимизации получили человеко-машинные процедуры. В отличие от других групп методов многокритериальной оптимизации, где мнение руководителя ( в дальнейшем лица, принимающего решение, или сокращенно ЛПР) о важности отдельных критериев в том или ином виде выявляется до решения конкретной задачи, человеко-машинные процедуры работают в диалоговом (интерактивном) режиме с ЛПР. Машинная программа, реализующая человеко-машинную процедуру, выводит информацию для ЛПР в виде распечаток или непосредственно на дисплей. ЛПР анализирует эту информацию и вырабатывает свои представления по поводу соотношения важности целей в конкурентной ситуации, в том числе и с учетом качественной, неформализуемой информации, затем эти новые предпочтения вводятся в ЭВМ и происходит их обработка. Далее для ЛПР вновь выводится информация, в которой учтено его предыдущее мнение, и цикл повторяется до тех пор, пока не будет получено решение, удовлетворяющее ЛПР. Различные человеко-машинные процедуры отличаются друг от друга видом информации, представляемой ЛПР на каждой итерации, а также формой, в которой ЛПР вырабатывает и вводит в ЭВМ предпочтения по важности целей. Выбор той или иной процедуры для решения конкретной задачи должен основываться на максимально полном удовлетворении следующих требований: обеспечение доверия ЛПРом; пригодность получаемой информации для принятия решения; высокая скорость сходимости решения.

Максимальное доверие к решению обеспечивают процедуры, в которых удается наиболее наглядно показать все альтернативные решения, обеспечить легкость использования и понимания метода работы человеко-машинной процедуры ЛПР, сходство действий ЛПР с методикой его работы без использования процедуры. Иллюстрацией работы человеко-машинной процедуры может быть пример использования модифицированной процедуры С. Зайонца и Ю. Валлениуса.

Укрупненный алгоритм модифицированной процедуры следующий.

1.Ввод исходной информации для расчета значений критериев 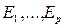и ограничений математической модели.

2. Присвоение начальных значений коэффициентам важности для свертки критериев оптимальности в единую целевую функцию вида (max и min в зависимости от смысла решаемой задачи). При этом должно выполняться условие 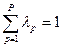. Для первой итерации допустимо задавать равные значения коэффициентов .

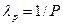3. Решение задачи отыскания оптимального решения (базового) решения модели на основе единой целевой функции

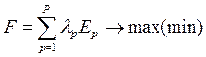. (3.9)

4. Генерация близких к базовому вариантов свертки критериев, которые получаются за счет последовательного увеличения каждого из коэффициентов важности в соответствии с отклонениями е.

Например, при наличии трех критериев оптимальности возможно формирование трех вариантов ( 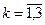), близких к базовому по критериям

,

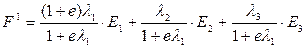если предполагается увеличение на величину е первого критерия;

,

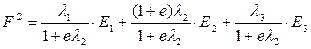если увеличивается второй критерий, и

при увеличении третьего критерия.

5. Решение задач отыскания оптимального решения для всех сгенерированных вариантов, близких к базовому, по вновь полученным в п. 4 целевым функциям и вывод на печать или дисплей базового или близки[ к енму вариантов решений.

6. Анализ базового или близких к нему вариантов решения ЛПР и ввод парных предпочтений для каждого из вариантов решений по отношению к базовому («+» – вариант более предпочтителен, чем базовое решения; «-» – вариант менее предпочтителен, чем базовое решение).

7. Если нет положительных предпочтений по вариантам решений, то вывод на печать значений критериев и переменных, которые являются оптимальными, и окончание работы процедуры.

8. Если есть положительные предпочтения по вариантам решений, формируются целевая функция и ограничения для решения вспомогательной задачи корректировки значений коэффициентов важности свертки критериев ( 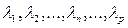) для следующей итерации поиска базового варианта. Целевая функция

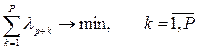. (3.10)

При этом ограничения при максимизации единой целевой функции имеют вид:

а) для каждого k-го варианта, который признан ЛПР более предпочтительным, чем базовый,

, (3.11)

где ξ – некое достаточно малое число, например, ξ =0,001; 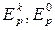– значение p-го критерия для k- го и базового вариантов соответственно;

б) для каждого k-го варианта, который признан ЛПР менее предпочтительным, чем базовый, записываются ограничения вида

; (3.12)

В) получивший набор значений должен соответствовать условию

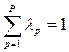. (3.13)

10. Получение новых значений коэффициентов свертки критериев ( 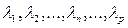) при решении математической модели (3.10) – (3.13) с помощью симплекс-метода и переход к блоку 3.

При минимизации единой целевой функции (3.9) ограничения (3.11) и (3.12) меняются местами.

В заключение отметим, что на этапе решения математической модели к ранее описанным ограничениям и допущениям могут добавляться допущения и ограничения, принятые при использовании полученной математической модели (например, ограничения, налагаемые используемой вычислительной техники, упрощения исходной математической модели для возможности применения аналитических методов и др.).

1. Раскройте основные положения и содержание этапов аналитического исследования при поиске оптимальных решений для однокритериальных моделей.

2. Раскройте основные положения и содержание этапов исследования при помощи численных методов в процессе поиска оптимальных решений для однокритериальных моделей.

3. Раскройте основные положения и содержание этапов экспериментальной оптимизации на ЭВМ при поиске оптимальных решений для однокритериальных моделей.

4. Представьте основные особенности организации поиска решений при наличии в модели случайных факторов

5. В чем заключается суть сведения стохастической задачи к детерминированной?

6. Каким образом метод статистического моделирования может быть применен для осреднения по результату в процессе поиска решений при наличии в модели случайных факторов? Приведите основные этапы алгоритма для решения этой задачи.

7. Опишите основные методы и подходы при реализации процедур принятия решений при наличии в модели неопределенных факторов

8. Что такое платежная матрица? Опишите ее структуру и назначение.

9. Опишите порядок нахождения решений в конфликтной ситуации при использовании моделей с неопределенными факторами. Представьте основные критерии, используемые при этом

10. Что такое многокритериальная оптимизация? Приведите классификацию типов задач многокритериальной оптимизации. Опишите основную суть методов многокритериальной оптимизации.

Глава 4.
ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

4.1. Особенности и принципы построения имитационных
моделей

Хотя классические оптимизационные методы и методы математического программирования являются мощным аналитическим средством, число реальных задач, которые можно сформулировать так, чтобы не возникало противоречий предположениям, лежащим в основе этих методов, сравнительно невелико. В связи с этим аналитические модели и в первую очередь модели математического программирования до настоящего времени не стали практическим инструментом управленческой деятельности.

Развитие вычислительной техники породило новое направление в исследовании сложных процессов – имитационное моделирование. Имитационные методы, являющиеся особым классом математических моделей, принципиально отличаются от аналитических тем, что ЭВМ в их реализации играют главную роль. ЭВМ третьего и тем более четвертого поколения обладают не только колоссальным быстродействием и памятью, но и развитыми внешними устройствами и совершенным программным обеспечением. Все это дает возможность эффективно организовать диалог человека и машины в рамках имитационной системы.

Идея метода имитационного моделирования состоит в том, что вместо аналитического описания взаимосвязей между входами, состояниями и выходами строят алгоритм, отображающий последовательность развития процессов внутри исследуемого объекта, а затем «проигрывают» поведение объекта на ЭВМ. Следует отметить, что, поскольку для имитационного моделирования зачастую требуются мощные ЭВМ, большие выборки статистических данных, издержки, связанные с имитацией, почти всегда высоки по сравнению с расходами, необходимыми для решения задачи на небольшой аналитической модели. Поэтому во всех случаях следует сопоставлять затраты средства и времени, потребные для имитации, с ценностью информации, которую ожидают получить.

Имитационная система – вычислительная процедура, формализованно описывающая изучаемый объект и имитирующая его поведение. При ее составлении нет необходимости упрощать описание явления, отбрасывая порой даже существенные детали, чтобы втиснуть его в рамки модели, удобной для применения тех или иных известных математических методов анализа. Для имитационного моделирования характерна имитация элементарных явлений, составляющих исследуемый процесс, с сохранением их логической структуры, последовательности протекания во времени, характера и состава информации о состояниях процесса. Модель по своей форме является логико-математической (алгоритмической).

Имитационные модели как подкласс математических моделей можно классифицировать на: статические и динамические; детерминированные и стохастические; дискретные и непрерывные.

Класс задачи предъявляет определенные требования к имитационной модели. Так, например, при статической имитации расчет повторяется несколько раз в различных условиях проведения эксперимента – исследование поведения «в определенный короткий период времени». При динамической имитации моделируется поведение системы «в течение продолжительного периода времени» без изменений условий. При стохастической имитации в модель включаются случайные величины с известными законами распределения; при детерминированной имитации эти возмущения отсутствуют, т.е. их влияние не учитывается.

Порядок построения имитационной модели и ее исследования в целом соответствует схеме построения и исследования аналитических моделей. Однако специфика имитационного моделирования приводит к ряду специфических особенностей выполнения тех или иных этапов. В литературе приводится следующий перечень основных этапов имитации:

1. Определение системы – установление границ, ограничений и измерителей эффективности системы, подлежащей изучению.

2. Формулирование модели – переход от реальной системы к некоторой логической схеме (абстрагирование).

3. Подготовка данных – отбор данных, необходимых для построение модели и представления их в соответствующей форме.

4. Трансляция модели – описание модели на языке, применяемом для используемой ЭВМ.

5. Оценка адекватности – повышение до приемлемого уровня степени уверенности, с которой можно судить относительно корректности выводов о реальной системе, полученных на основании обращения к модели.

6. Стратегическое планирование – планирование эксперимента, который должен дать необходимую информацию.

7. Тактическое планирование – определение способа проведения каждой серии испытаний, предусмотренных планом эксперимента.

8. Экспериментирование – процесс осуществления имитации с целью получения желаемых данных и анализа чувствительности.

9. Интерпретация – построение выводов по данным, полученным путем имитации.

10. Реализация – практическое использование модели и (или) результатов моделировании.

11. Документирование – регистрация хода осуществление проекта и его результатов, а также документирование процесса создания и использования модели

Документирование близко связано с реализацией. Тщательное и полное документирование процессов разработки и экспериментирования с моделью позволяет значительно увеличить срок ее жизни и вероятность успешной реализации, облегчает модификацию модели и обеспечивает возможность ее использования, если даже подразделений, занимающихся разработкой модели, больше не существует, может помочь разработчику модели учиться на своих ошибках.

Как видно из приведенного перечня, особо выделены этапы планирования экспериментов на модели. И это не удивительно. Ведь имитация на ЭВМ – это эксперимент. Анализ и поиск оптимальных решений алгоритмических моделей (а все имитационные модели относятся к этому классу) осуществляется теми или иными методами экспериментальной оптимизации на ЭВМ. Единственное отличие имитационного эксперимента от эксперимента с реальным объектом состоит в том, что имитационный эксперимент производится с моделью реальной системы, а не с самой системой.