Использование методов экспертной оценки

Экспертные оценки это количественные или порядковые оценки процессов или явлений, не поддающихся непосредственному измерению. Сущность метода экспертных оценок заключается в проведении экспертами интуитивно-логического анализа исследуемой ситуации с количественной оценкой суждений и формальной обработкой результатов экспертизы. Получаемое в результате обработки обобщенное мнение экспертов принимается как решение проблемы.

Для проведения экспертизы должна быть сформулирована группа специалистов-организаторов экспертизы, призванная обеспечить условия для эффективной деятельности экспертов, разработать процедуру экспертизы, наиболее соответствующую характеру данной проблемы. В задачи группы входят: постановка проблемы, определение целей и задач экспертизы, ее границ, основных этапов; разработка процедуры экспертизы; отбор экспертов , проверка их компетентности и формирование групп экспертов; проведение опроса и согласование оценок; формализация полученной информации, ее обработка, анализ и интерпретация.

Существует множество методов экспертных оценок (индивидуальных и коллективных) с соответствующими процедурами обработки многих экспертов. Для задачи выбора существенных факторов наиболее пригодны методы ранга устанавливающие различного рода приоритеты между факторами. Приоритет факторов может задаваться различными способами. Распространены следующие характеристики приоритета.

Ряд приоритета J представляет собой упорядоченное множество индексов отдельных факторов J = (1, 2,…,n) и отражает чисто качественные отношения доминирования факторов, а именно: фактор x₁ важнее фактора x₂, фактор x₂ важнее фактора x₃ и т.д. Количественная сторона доминирования при этом не указывается.

При наличии группы равнозначных факторов (например, x₃ и x₄) их выделяют в ряду приоритета J внутренними скобками:

.

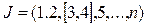Вектор приоритета 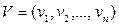представляет собой n-мерный вектор, компонентами v_i которого являются бинарные отношения приоритета. Бинарное отношение приоритета определяет степень превосходства по важности двух соседних факторов x_i и x_i+1 из ряда приоритета J , т.е. во сколько раз фактор x_i важнее фактора x_i+1 . Для равнозначных факторов x_k и x_k+1 ( так же как и для последнего фактора x_n ) соответствующая компонента v_k =1
( v_n=1).

Вектор приоритета V определяется в результате попарного сравнения факторов, предварительно упорядоченных в соответствии с рядом приоритета J, причем .

Вектор весовых коэффициентов 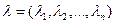представляет собой n-мерный вектор, компоненты которого связаны соотношением

; .

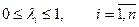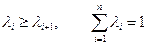Для расчета любой из характеристик J, V, 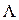в принципе можно применять аналогичные методы экспертной оценки. Рассмотрим один из простейших методов экспертной оценки, используемой для определения вектора весовых коэффициентов .

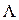При методе полного попарного сравнения факторов эксперты устанавливают только ряд приоритетов J и вектор приоритета V. Соседние компоненты 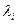и 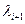вектора весовых коэффициентов связаны соотношением

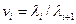. (2.10)

Выражение (2.10) позволяет при задании ряда приоритета J и вектора приоритета V рассчитать каждую компоненту вектора 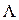по формуле

.

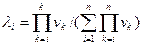Например, если заданы три фактора, упорядоченные рядом приоритета J = (1. 2.3) и оценивание с помощью вектора V = (2, 3, 1), то

,

,

.

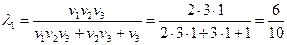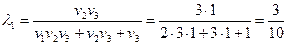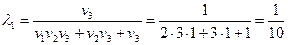После расчетов весовых коэффициентов 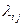по каждому j- му эксперту ( 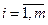) определяют среднее арифметическое значение весового коэффициента для каждого i-го фактора: .

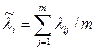Косвенным показателем согласованности мнений экспертов по оценке данного фактора служит коэффициент вариации, выраженный в процентах:

.

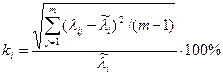Чем меньше вариация, тем больше согласованность мнений экспертов. Основным показателем, отражающим степень согласованности мнений экспертов по всей совокупности факторов, служит коэффициент конкордации.

Определив, что мнение экспертов согласованы между собой, на основании совместного анализа средних арифметических значений 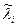и коэффициента вариации 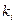проводят окончательный выбор существенных факторов.

Для оценки большого количества факторов и предотвращения резкого снижения достоверности оценок из-за невозможности объективно оценивать одновременно все факторы применяют специальные процедуры опроса экспертов, например группировки факторов по объединяющим признакам. В этом методе вся совокупность факторов классифицируется по какому-либо признаку на группы числом не более 7. Если число факторов в группе превышает 7, то их опять классифицируют по новому, более детальному признаку, соблюдая то же самое ограничение на число подгрупп и число факторов в подгруппах. После классификации (например, двухуровневой) проводят ряд экспертиз, последовательно оценивающих важность отдельных групп между собой, отдельных подгрупп внутри группы, отдельных факторов внутри подгруппы. Небольшое число признаков, оцениваемых в каждой экспертизе, обеспечивает высокую достоверность их оценки. Итоговый весовой коэффициент фактора определяется как произведение весового коэффициента фактора в подгруппе, весового коэффициента подгруппы в группе, весового коэффициента группы в совокупности групп.

Хотя число экспертиз при описанном методе достаточно велико, но зато для проведения каждой из них может привлекаться свой контингент экспертов, хорошо знающих именно этот круг частных вопросов, что еще более повысит достоверность их оценок.

В результате взаимодополняющего использования вышеописанных статистических и экспертных методов исследователь формирует ряд приоритета для анализируемого множества факторов. На основании этого ряда им отбирается для построения математической модели ограниченное число факторов, вариации которых он считает действительно существенными. Исследователь в этом отношении должен руководствоваться также собственной интуицией. При дальнейшем исследовании объекта по математической модели, как правило, возникает необходимость в корректировке состава существенных факторов модели. Поэтому упомянутый выше выбор существенных факторов представляет собой лишь предварительную наметку.