Методы отбора существенных факторов модели

При отборе существенных факторов используют два основных типа методов:

1. Статистические методы, позволяющие на основании имеющегося статистического материала количественно оценить степень влияния факторов друг на друга и на результат.

2. Экспертные методы, при которых опыт специалистов и знания сущности исследуемого объекта позволяют оценить существенность факторов.

Использование методов математической статистики

Как было отмечено ранее, на результат функционирования системы влияют не только факторы, поддающиеся прямому количественному измерению, но и факторы, такому измерению не поддающиеся, – порядковые и классификационные качественные факторы. Для них исследователь устанавливает несколько градаций шкалы измерений (уровней). Эти уровни могут быть принципиально упорядочены, например для фактора»удобство обслуживания» – малое, среднее и высокое, и не упорячдочены, например для факторов «порядок обслуживания станков-автоматов» – неупорядоченное обслуживание станков, приоритетная загрузка слесарей-ремонтников.

Качественный фактор является существенным только в том случае, если существует два (или более) уровня (группы уровней), для которых существенно различаются выходные характеристики объекта. Так, например, исследования могут показать, что объем выпуска продукции на участке станков-автоматов существенно различаются по фактору «порядок обслуживания» для уровня «приоритетная загрузка слесарей-ремонтников» и уровней «неупорядоченное обслуживание» и «приоритетное обслуживание станков», а между последними уровнями неразличим. Для учета различимых уровней (групп уровней) качественных факторов требуется построение различных моделей функционирования одного и того же объекта. В связи с этим еще до начала построения модели требуется решать, необходимо ли включение в модель того или иного качественного фактора в качестве существенного, т.е. нужно ли в дальнейшем строить систему моделей, каждая из которых описывает тот или иной уровень интересующего исследователя качественного фактора.

Такое исследование проводится с помощью дисперсионного анализа, в процессе использования которого исследователь проверяет ряд гипотез. Прежде всего, выдвигается и проверяется гипотеза о равенстве выходных характеристик для всех уровней качественного фактора, другими словами, гипотеза о невыявлении качественного фактора на моделируемый процесс. Если эта гипотеза опровергается, то, следовательно есть некоторые уровни качественных факторов, существенно влияющие на результаты моделирования. В связи с этим проверяются гипотезы о равенстве выходных характеристик при попарном сравнении различных уровней качественных факторов между собой. Проверка подобных гипотез позволяет установить, какие уровни факторов неразличимы между собой, т.е. их можно рассматривать как один уровень, и какие отличаются друг от друга.

После выявления различимых, а следовательно, существенных уровней качественного фактора для каждого различимого уровня (группы уровней) подготавливается статистическая информация (табл.2.3.), а затем решается задача выявления взаимосвязи между входными количественными факторами, за счет чего сокращается количество независимых факторов.

Таблица 2.3. Представление статистических данных для отбора

Существенных факторов

№ эксперимента	Входные факторы	Выходные факторы
х1	х2	…	хn	w1	w2	…	wk
	х11	х12	…	х1n	w11	w12	…	w1k
	х21	х22	…	х2n1	w21	w22	…	w2k
…	…	…	…	…	...	...	…	…
N	хN1	хN2	…	хNn	wN1	wN2	…	wNk

При решении этой задачи из множества факторов x₁,x₂,…,x_n выделяют такие факторы, у которых значение коэффициента парной корреляции или корреляционного отношения не менее 0,8. Подобные факторы называются коллинеарными.

Коэффициент парной корреляции r_ij характеризует степень линейной зависимости между двумя факторами x_i и x_j , а корреляционное отношение 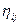– степень нелинейной зависимости. Формулы расчета этих величин приводятся в литературе по математической статистике. Коэффициенты r_ij и 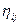характеризуются следующими соотношениями:

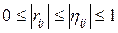; (2.8)

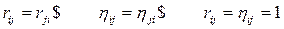. (2.9)

Значения r_ij и 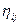, близкие к нулю, указывают на отсутствие взаимосвязи факторов, а близость их к единице – на наличие функциональной связи. Для определения коллинеарных факторов вычисляется матрица коэффициентов парной корреляции r_ij .

Вследствие симметричности (2.9) анализу подвергается только одна половина матрицы. При наличии пары коллинеарных факторов в модели как независимый целесообразно использовать фактор, имеющий меньшую дисперсию, а значение другого фактора вычислять по выявленной регрессионной зависимости. Если ни один из элементов матрицы 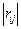не превосходит 0,8, целесообразно вычислить матрицу корреляционных отношений 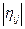, но их расчет требует более громоздких вычислений.

Далее решается задача выявления взаимосвязи между входными факторами и выходными характеристиками модели и выбора из входных факторов, наиболее существенно влияющих на результаты моделирования.

При решении этой задачи для входных количественных факторов 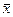, отобранных на первом этапе, и выходных факторов 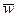вычисляют матрицу парных коэффициентов линейной корреляции 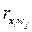либо корреляционных отношений 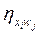. Упорядоченные по значению корреляционных коэффициентов факторы 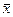могут служить основой для выбора множества существенных факторов. Однако в ряде случаев изучаемые факторы лишь в косвенной форме отражают наиболее существенные, но не поддающиеся непосредственному наблюдению и измерению внутренние, скрытые свойства объекта, что проявляется в незначительных значениях практически всех парных корреляционных коэффициентов ( ).

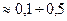В такого рода ситуациях с помощью достаточно сложного математического аппарата факторного анализа пытаются выявить наибольшее число латентных переменных, на базе которых в дальнейшем и строится математическая модель.