Роль и место моделирования в исследовании систем.

Пояснительная записка

к курсовой работе

по дисциплине: «Моделирование экономическихпроцессов».

Основные особенности применения

вероятностно-статистических методов для моделирования экономических систем.

Руководитель:Выполнила:

Профессор студентка группы 05-ИЭ-2

Арунянц Г.Г Орлова Е.

Ерохина Е.

-------------------------- --------------------------

(подпись) (подпись)

«------ »-----------2008 «------ »-----------2008

Калининград,2008

1. Содержание

1. Содержание.

2. Введение.

3. Роль и место моделирования в исследовании систем.

4. Классификация моделей.

5. Основы вероятно-статистического метода.

6. Моделирование случайных величин.

7. Теория массового обслуживания. Основные положения.

7.1. Предмет и задачи теории массового обслуживания.

7.2. Система массового обслуживания.

7.3. Классификация СМО.

7.4. Характеристики СМО.

8. Разыгрывание непрерывной случайной величины.

9. Моделирование систем и языки программирования.

10. Заключение.

11. Список используемой литературы.

Введение

Метод статистического моделирования (или метод Монте-Карло) — это способ исследования поведения вероятностных систем (экономических, технических и т. д.) в условиях, когда не известны в полной мере внутренние взаимодействия в этих системах

.

Этот метод заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Одно такое воспроизведение функционирования системы называют реализацией, или испытанием. После каждого испытания регистрируют совокупность параметров, характеризующих случайный исход реализации.

Метод основан на многократных испытаниях построенной Модели с последующей статистической обработкой полученных данных с целью определения числовых характеристик рассматриваемого процесса в виде статистических оценок его параметров.

Процесс моделирования функционирования экономической системы сводится к машинной имитации изучаемого процесса, который как бы копируется на ЭВМ со всеми сопровождающими его случайностями.

Первые сведения о методе Монте-Карло были опубликованы в конце 1940-х гг Авторами метода являются американские математики Дж. Нейман и С. Улам. В нашей стране первые работы были опубликованы в 1955—1956 гг В.В. Чавчанидзе, Ю.А. Шрейдером и B.C. Владимировым.

Классификация моделей.

Физические модели.В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на 2 группы — физические и абстрактные (математические).

Ф.М. обычно называют систему, эквивалентную или подобную оригиналу, но возможно имеющую другую физическую природу. Виды Ф.М.:

- натуральные;

- квазинатуральные;

- масштабные;

- аналоговые;

Натуральные модели— это реальные исследуемые системы (макеты, опытные образцы). Имеют полную адекватность (соответствия) с системой оригиналом, но дороги.

Квазинатуральные модели— совокупность натуральных и математических моделей.

Этот вид используется тогда, когда модель части системы не может быть математической из-за сложности её описания (модель человека оператора) или когда часть системы должна быть исследована во взаимодействии с другими частями, но их ещё не существует или их включение очень дорого. (вычислительные полигоны, АСУ)

Масштабная модель— это система той же физической природы, что и оригинал, но отличается от него масштабами. Методологической основой масштабного моделирования является теория подобия. При проектировании ВС масштабные модели могут использоваться для анализа вариантов компоновочных решений.

Аналоговыми моделяминазывают системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрические системы. Аналоговое моделирование использует при исследовании средства ВТ на уровне логических элементов и электрических цепей, а так же на системном уровне, когда функционирование системы описывается например, дифференциальными или алгебраическими уравнениями.

Математические модели.Математические модели представляют собой формализованное представление системы с помощью абстрактного языка, с помощью математических соотношений, отражающих процесс функционирования системы. Для составления математических моделей можно использовать любые математические средства — алгебраическое, дифференциальное, интегральное исчисления, теорию множеств, теорию алгоритмов и т.д. По существу вся математика создана для составления и исследования

моделей объектов и процессов.

К средствам абстрактного описания систем относятся также языки химических формул, схем, чертежей, карт, диаграмм и т.п. Выбор вида модели определяется особенностями изучаемой системы и целями моделирования, т.к. исследование модели позволяет получить ответы на определённую группу вопросов.

Для получения другой информации может потребоваться модель другого вида. Математическое модели можно классифицировать на детерминированные и вероятностные, аналитические, численные и имитационные.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения (1.2) в явном виде, используя известный математический аппарат.

Численная модель характеризуется зависимостью (1.2) такого вида, который допускает только частные решения для конкретных начальных условий и количественных параметров моделей.

Имитационная модель — это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные. Поскольку для реализации имитационных моделей служат ВС, средствами формализованного описания ИМ

служат универсальные и специальные алгоритмические языки. ИМ в наибольшей степени подходят для исследования ВС на системном уровне.

Пример.

Разыграть 8 значений дискретной случайной величины Х, закон распределения

которой задан в виде таблицы:

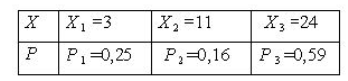
Решение

1. Разобьем интервал (0,1) оси Оr точками с координатами 0,25; 0,25+0,16=0,41 на

три частичных интервала;

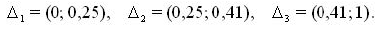
2. Выпишем из таблицы случайных чисел 9 чисел, например 0,10; 0,37; 0,08; 0,99;

0,12; 0,66; 0,31; 0,85.

3. Случайное число r1 = 0,10 принадлежит первому частичному интервалу, поэтому

разыгрываемая случайная величина приняла возможное значение x1 = 3.

Случайное число r2= 0,37 принадлежит второму частичному интервалу, поэтому

разыгрываемая величина приняла возможное значение x2 = 11. Аналогично

получим остальные возможные значения дискретной случайной величины Х.

Итак: разыгранные возможные значения Х таковы: 3; 11; 3; 24; 3; 24; 11; 24.

Как видим, можно получить множество значений случайной величины Х с

заданным законом распределения.

Классификация СМО.

Для облегчения процесса моделирования используют классификацию СМО по

различным признакам, для которых пригодны определенные группы методов и моделей теории СМО, упрощающие подбор адекватных математических моделей

Характеристики СМО.

Перечень характеристик систем массового обслуживания можно представить следующим

образом:

Ø среднее время обслуживания;

Ø среднее время ожидания в очереди;

Ø среднее время пребывания в СМО;

Ø средняя длина очереди;

Ø среднее число заявок в СМО;

Ø количество каналов обслуживания;

Ø интенсивность входного потока заявок;

Ø интенсивность обслуживания;

Ø интенсивность нагрузки;

Ø коэффициент нагрузки;

Ø относительная пропускная способность;

Ø абсолютная пропускная способность;

Ø доля времени простоя СМО;

Ø доля обслуженных заявок;

Ø доля потерянных заявок;

Ø среднее число занятых каналов;

Ø среднее число свободных каналов;

Ø коэффициент загрузки каналов;

Ø среднее время простоя каналов.

Пример.

Разыграть 3 возможных значения непрерывной случайной величины Х,

распределенной равномерно в интервале (2; 10).

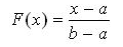Решение

Функция распределения величины Х имеет следующий вид:

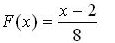
По условию, a = 2, b = 10, следовательно,

В соответствии с алгоритмом разыгрывания непрерывной случайной величины

приравняем F(X) выбранному случайному числу ri.. Получим отсюда:

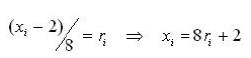(5.3)

Далее в соответствии с алгоритмом выберем три случайных числа, распределенных

равномерно в интервале (0; 1). Например r1 = 0,11; r2 = 0,17; r3 = 0,66.

Подставим эти числа в уравнение (5.3).Получим соответствующие возможные

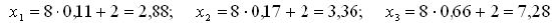значения х :

Пояснительная записка

к курсовой работе

по дисциплине: «Моделирование экономическихпроцессов».

Основные особенности применения

вероятностно-статистических методов для моделирования экономических систем.

Руководитель:Выполнила:

Профессор студентка группы 05-ИЭ-2

Арунянц Г.Г Орлова Е.

Ерохина Е.

-------------------------- --------------------------

(подпись) (подпись)

«------ »-----------2008 «------ »-----------2008

Калининград,2008

1. Содержание

1. Содержание.

2. Введение.

3. Роль и место моделирования в исследовании систем.

4. Классификация моделей.

5. Основы вероятно-статистического метода.

6. Моделирование случайных величин.

7. Теория массового обслуживания. Основные положения.

7.1. Предмет и задачи теории массового обслуживания.

7.2. Система массового обслуживания.

7.3. Классификация СМО.

7.4. Характеристики СМО.

8. Разыгрывание непрерывной случайной величины.

9. Моделирование систем и языки программирования.

10. Заключение.

11. Список используемой литературы.

Введение

Метод статистического моделирования (или метод Монте-Карло) — это способ исследования поведения вероятностных систем (экономических, технических и т. д.) в условиях, когда не известны в полной мере внутренние взаимодействия в этих системах

.

Этот метод заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Одно такое воспроизведение функционирования системы называют реализацией, или испытанием. После каждого испытания регистрируют совокупность параметров, характеризующих случайный исход реализации.

Метод основан на многократных испытаниях построенной Модели с последующей статистической обработкой полученных данных с целью определения числовых характеристик рассматриваемого процесса в виде статистических оценок его параметров.

Процесс моделирования функционирования экономической системы сводится к машинной имитации изучаемого процесса, который как бы копируется на ЭВМ со всеми сопровождающими его случайностями.

Первые сведения о методе Монте-Карло были опубликованы в конце 1940-х гг Авторами метода являются американские математики Дж. Нейман и С. Улам. В нашей стране первые работы были опубликованы в 1955—1956 гг В.В. Чавчанидзе, Ю.А. Шрейдером и B.C. Владимировым.

Роль и место моделирования в исследовании систем.

Познание любой системы сводится по существу к созданию её модели. Перед изготовлением каждого устройства или сооружения разрабатывается его модель - проект. Любое произведение искусства является моделью, фиксирующее действительность.

Достижения математики привели к распространению математических моделей различных объектов и процессов. Подмечено, что динамика функционирования разных по физической природе систем однотипными зависимостями, что позволяет моделировать их на ЭВМ.

На качественно новую ступень поднялась моделирование в результате разработки методологии имитационного моделирования на ЭВМ.

Сейчас трудно указать область человеческой деятельности, где бы применялось моделирование. Разработаны модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, атомного взрыва, последствий атомной войны.

Специалисты считают, что моделирование становится основной функцией ВС. На практике широко используются АСУ технологическими процессами организационно-экономическими комплексами, процессами проектирования, банки данных и знаний. Но любая из этих систем нуждается в информации об управляемом объекте и модели управляемого объекта, в моделировании тех или иных управляющих решений.

Сами ВС как сложные и дорогостоящие технические системы могут являться объектами моделирования.

Обычно процесс разработки сложной системы осуществляется итерационно с использованием моделирования проектных решений. Если характеристики не удовлетворяют предъявленным требованиям, то по результатам анализа производят корректировку проекта, затем снова проводят моделирование.

При анализе действующих систем с помощью моделирования определяют границы работоспособности системы, выполняют имитацию экспериментальных условий, которые могут возникнуть в процессе функционирования системы. Искусственное создание таких условий на действительной системе затруднено и может привести к катастрофическим последствиям.

Применение моделирования может быть полезным при разработке стратегии развития ВС, её усовершенствования при создании сетей ЭВМ.

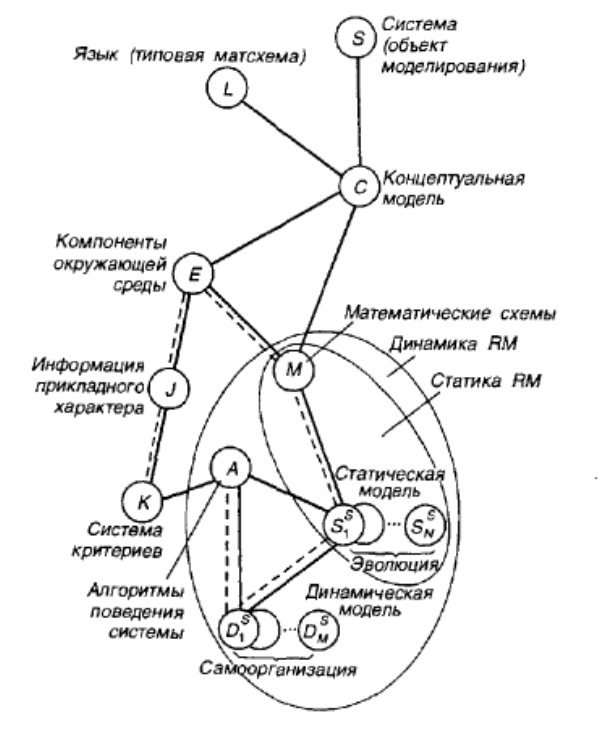
Рис. 1

Классификация моделей.

Физические модели.В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на 2 группы — физические и абстрактные (математические).

Ф.М. обычно называют систему, эквивалентную или подобную оригиналу, но возможно имеющую другую физическую природу. Виды Ф.М.:

- натуральные;

- квазинатуральные;

- масштабные;

- аналоговые;

Натуральные модели— это реальные исследуемые системы (макеты, опытные образцы). Имеют полную адекватность (соответствия) с системой оригиналом, но дороги.

Квазинатуральные модели— совокупность натуральных и математических моделей.

Этот вид используется тогда, когда модель части системы не может быть математической из-за сложности её описания (модель человека оператора) или когда часть системы должна быть исследована во взаимодействии с другими частями, но их ещё не существует или их включение очень дорого. (вычислительные полигоны, АСУ)

Масштабная модель— это система той же физической природы, что и оригинал, но отличается от него масштабами. Методологической основой масштабного моделирования является теория подобия. При проектировании ВС масштабные модели могут использоваться для анализа вариантов компоновочных решений.

Аналоговыми моделяминазывают системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрические системы. Аналоговое моделирование использует при исследовании средства ВТ на уровне логических элементов и электрических цепей, а так же на системном уровне, когда функционирование системы описывается например, дифференциальными или алгебраическими уравнениями.

Математические модели.Математические модели представляют собой формализованное представление системы с помощью абстрактного языка, с помощью математических соотношений, отражающих процесс функционирования системы. Для составления математических моделей можно использовать любые математические средства — алгебраическое, дифференциальное, интегральное исчисления, теорию множеств, теорию алгоритмов и т.д. По существу вся математика создана для составления и исследования

моделей объектов и процессов.

К средствам абстрактного описания систем относятся также языки химических формул, схем, чертежей, карт, диаграмм и т.п. Выбор вида модели определяется особенностями изучаемой системы и целями моделирования, т.к. исследование модели позволяет получить ответы на определённую группу вопросов.

Для получения другой информации может потребоваться модель другого вида. Математическое модели можно классифицировать на детерминированные и вероятностные, аналитические, численные и имитационные.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения (1.2) в явном виде, используя известный математический аппарат.

Численная модель характеризуется зависимостью (1.2) такого вида, который допускает только частные решения для конкретных начальных условий и количественных параметров моделей.

Имитационная модель — это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные. Поскольку для реализации имитационных моделей служат ВС, средствами формализованного описания ИМ

служат универсальные и специальные алгоритмические языки. ИМ в наибольшей степени подходят для исследования ВС на системном уровне.