Условия прочности и жесткости

Определение наибольших внутренних усилий не решает однозначно задачи расчета на прочность, так как за прочность конструкции отвечает не непосредственно усилие, а мера интенсивности этого усилия в поперечном сечении, то есть напряжение.

Механическое напряжение – это внутреннее усилие, приходящееся на единицу площади сечения. Оно измеряется в паскалях: 1Па=1Н/м². В практических расчетах удобнее пользоваться краткой единицей – мегапаскаль.

1 МПа = 10⁶ Па = 1 Н/мм² » 10 кгс/см² = 0,1 кгс/мм².

Если обозначить 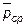– среднее напряжение в точке К на элементарной площадке ∆А (рис.3,а)

,

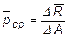где ∆R – равнодействующая внутренних усилий на площадке ∆А, то истинным полным напряжением в точке K будет

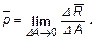(11)

Его проекциями на координатные оси являются соответственно нормальное ( 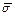) и касательные ( 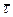) напряжения:

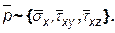(12)

В расчетах на прочность используются только эти два вида напряжений, так как материалы по разному реагируют на них. Этим напряжениям соответствуют два вида деформаций, то есть изменений размеров и формы бесконечно малого объема: линейные e (рис. 3,б) и угловые (сдвига) g(рис. 3,в).

При расчетах инженерных конструкций в первую очередь проверяют их прочность. Для расчета на прочность конструкций необходимо:

1. Определить характер распределения внутренних усилий по длине бруса, то есть построить их эпюру и найти опасное сечение.

2. Найти опасную точку в поперечном сечении и вычислить максимальные напряжения в ней, которые равны отношению

внутреннего усилия к соответствующему геометрическому параметру поперечного сечения, зависящему от его формы и размеров.

3. Сравнить максимальные напряжения с допускаемыми для данного вида материала:

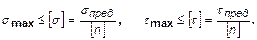(13)

Здесь 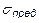, 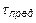– предельные или опасные напряжения для материала, при котором деталь перестает выполнять свои функции, то есть теряет прочность. Эти напряжения зависят от вида материала и определяются при механических испытаниях. Для пластичных материалов опасными являются напряжения текучести σ_т,t_Т, при которых резко увеличиваются пластические деформации при неизменной нагрузке. Для хрупких материалов в качестве опасного принимается предел прочности σ_в, t_В (временное сопротивление) – максимальное напряжение, которое способен выдержать образец из данного материала не разрушаясь.

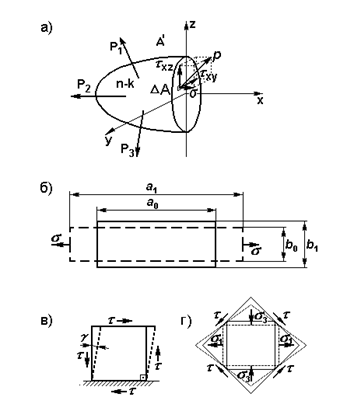
Рис. 3. Напряжения и деформации:

а – нормальное и касательные напряжения в сечении; б – продольная и поперечная деформации; в – деформация сдвига; г – связь линейных и угловых деформаций

[n] – нормативный коэффициент запаса прочности. Вводится на основе опыта эксплуатации аналогичных конструкций, учитывает возможные неблагоприятные отклонения в работе конструкции от расчетных и вид; [n] >1.

[σ], [t] - допускаемые напряжения, которые определяются как конкретная доля предельных напряжений:

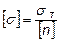– для пластичного материала,

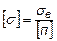– для хрупкого материала.

Для стальных конструкций средние значения пределов составляют: σ_т =240 МПа, σ_в =340 МПа, t_Т =120 МПа, [n]=1,5 (по отношению к σ_т иt_Т), откуда [σ]=160 МПа, [t]=80 МПа.

По условию прочности возможно решение трех вариантов задач:

1. Проверочный расчет – проверка выполнения условия прочности.

2. Расчет на грузоподъемность – определение допускаемой (максимально возможной) нагрузки.

3. Проектный расчет – определение размеров поперечного сечения.

При расчете некоторых конструкций одновременно с условием прочности или вместо него необходимо выполнение условия жесткости, то есть условия недопустимости больших перемещений. Перемещения поперечных сечений стержней определяются относительными деформациями материала всего стержня (линейными и угловыми) с учетом опорных условий. Относительные деформации зависят от соответствующих напряжений и косвенно от внутренних усилий, действующих в поперечных сечениях стержня.

Относительная продольная деформация ε (рис 3,б) вычисляется в виде

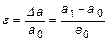, (14)

гдеΔа – абсолютное удлинение, а₁, а₀ – длина элемента в деформированном и начальном состояниях.

Относительная поперечная деформация (относительное поперечное сужение) определяется (рис. 3,б) в виде

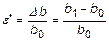. (15)

Между продольной и поперечной деформациями существует взаимосвязь вида

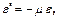(16)

где μ – коэффициент поперечной деформации (Пуассона), зависящий от вида материала; 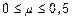. Для стальных конструкций, например, среднее значениеμ=0,25.

В случае простого напряженного состояния упругие линейные e (рис. 3,б) и угловые g (рис. 3,в) деформации, описывающие изменения размеров и формы бесконечно малого объема нагруженного тела, определяют по законуГука через нормальные и касательные напряжения.

(17)

Здесь Е и G – соответственно модули упругости материала первого и второго рода. Например, для стали их среднее значение составляет: Е = 2×10⁵ МПа, G=8×10⁴ МПа.

На рис. 3,г на примере напряженного состояния чистого сдвига показано, что линейные и угловые деформации бесконечно малого объема взаимосвязаны, так как здесь диагонали элемента имеют только линейные деформации: одна удлиняется, другая укорачивается. При этом величина деформаций и, соответственно, величина напряжений в нагруженном теле зависят от положения элемента тела (ориентации сечений).