Теория пластичности и ползучести

ТЕОРИЯ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ

Часть 3. Теории пластичности

Содержание

1. Деформационная теория при одноосном растяжении

2. Деформационная теория при сложном нагружении

3. Пластическая деформация

4. Модель идеальной пластичности при одноосном растяжении

5. Ассоциированный закон пластического течения

6. Теория идеальной пластичности при сложном нагружении

7. Теория течения с изотропным упрочнением

8. Теория течения с трансляционным упрочнением

9. Обзор моделей пластичности в пакетах прикладных программ

10. Область применения моделей пластичности

Пластическая деформация

Получив кривую деформирования при начальном нагружении образцов материала, нельзя обнаружить, является ли материал упругим или нет. Свойство пластичности обнаруживается только после разгрузки на основе наличия остаточной деформации 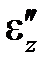(рис.4.3). Процесс разгрузки, практически отвечает линейной функции

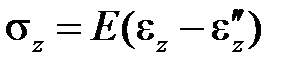, (3.1)

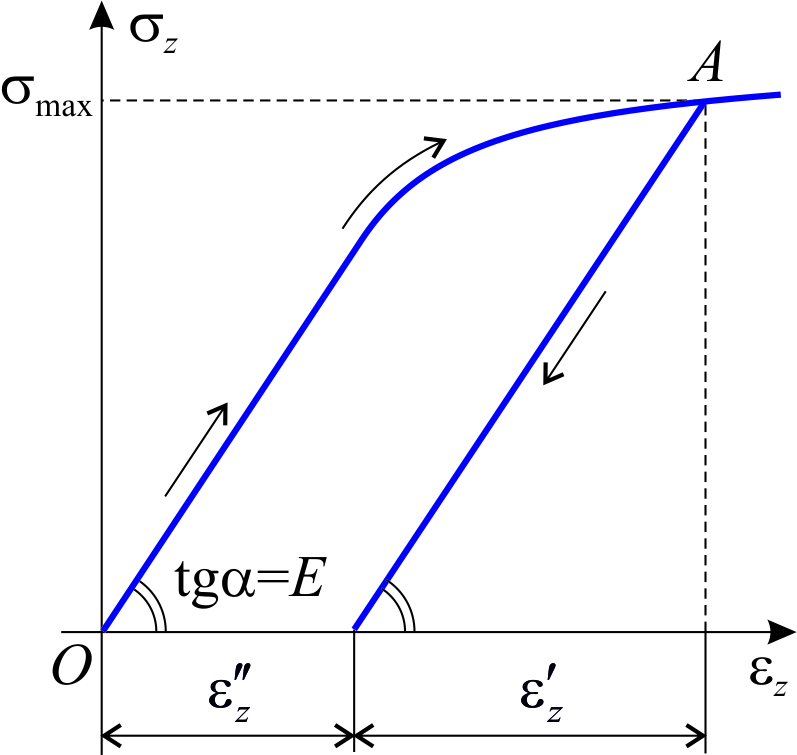Рис.3.1

где модуль E почти тот же, что и модуль Юнга в пределах упругости, когда напряжения достаточно малы. Поэтому разность, стоящую в скобках выражения (3.1), стали называть упругой деформацией

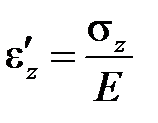. (3.2)

Далее мы будем использовать это выражение независимо от экспериментальных наблюдений (в частности, разгрузку образца можно выполнить не всегда). Заметим, что название «упругая деформация» чисто условно, так как применено к неупругому телу; правильнее было бы назвать его «линейной» деформацией, поскольку это величина, линейно связанная с напряжением (подобно деформации линейно упругого тела). Модуль упругости – это константа материала, поэтому величина (s_z /E) может рассматриваться как безразмерное напряжение, масштабированное с помощью постоянной величины E.

Разность 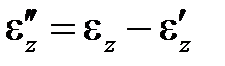называют пластической, или неупругой деформацией; в неизотермическом случае

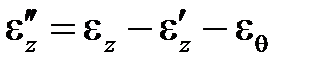. (3.3)

Это тоже условное название; правильнее было бы назвать эту величину нелинейной деформацией, отличающей полную деформацию от линейной. Заметим, что выражение 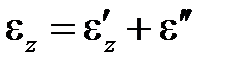или

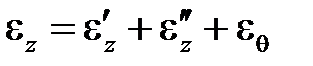(3.4)

(в неизотермическом случае) иногда называют физическим уравнением, заменяющим закон Гука. В действительности это просто следствие двух введенных определений для упругой и неупругой деформации, не имеющих отношения к свойствам материала. Несмотря на такую «нефизичность», разделение полной деформации на слагаемые оказывается удобным. В частности, для ситуации на рис.3.1 можно констатировать, что при нагружении пластическая деформация растет, а в процессе разгрузки не изменяется.

При исследовании деформационных свойств материалов задают напряжение (или деформацию) и следят за изменением деформации (или напряжения); свойства материала при этом не зависят от того, какое производится нагружение: мягкое или жесткое. В любом случае, опираясь на линеаризованное физическое уравнение (3.4), мы следим в действительности за эволюцией пластической деформации. Все модели неупругих материала, так или иначе, определяют закон для величины 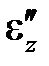. Более того, и упругое тело можно определить таким законом: например, физическое уравнение 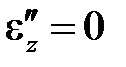отвечает закону Гука. Закон 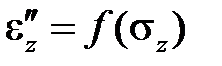или 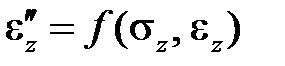отвечает нелинейно упругому телу, поскольку означает однозначную связь между напряжениями и деформациями.

При сложном напряженно-деформированном состоянии мерой упругой деформации является двухвалентный тензор

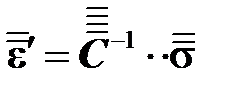, (3.5)

неупругая деформация определяется следующим образом

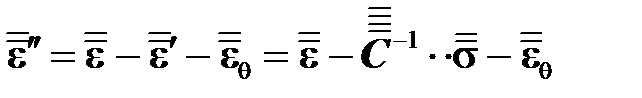, (3.6)

а физическое уравнение имеет вид

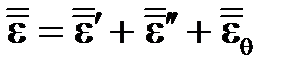. (3.7)

Примеры реализации моделей пластичности в пакете ANSYS

1. The Bilinear Kinematic Hardening (BKIN).

MPTEMP,1,0,500 ! Define temperatures for Young's modulusMP,EX,1,12E6,-8E3 ! C0 and C1 terms for Young's modulusTB,BKIN,1,2 ! Activate a data tableTBTEMP,0.0 ! Temperature = 0.0TBDATA,1,44E3,1.2E6 ! Yield = 44,000; Tangent modulus = 1.2E6TBTEMP,500 ! Temperature = 500TBDATA,1,29.33E3,0.8E6 ! Yield = 29,330; Tangent modulus = 0.8E6TBLIST,BKIN,1 ! List the data table/XRANGE,0,0.01 ! X-axis of TBPLOT to extend from =0 to 0.01TBPLOT,BKIN,1 ! Display the data table

2. The Multilinear Kinematic Hardening (MKIN)

MPTEMP,1,0,500 ! Define temperature-dependent EX,MP,EX,1,12E6,-8E3 ! as in above exampleTB,MKIN,1,2 ! Activate a data tableTBTEMP,,STRAIN ! Next TBDATA values are strainsTBDATA,1,3.67E-3,5E-3,7E-3,10E-3,15E-3 ! Strains for all tempsTBTEMP,0.0 ! Temperature = 0.0TBDATA,1,44E3,50E3,55E3,60E3,65E3 ! Stresses at temperature = 0.0TBTEMP,500 ! Temperature = 500TBDATA,1,29.33E3,37E3,40.3E3,43.7E3,47E3 ! Stresses at temperature = 500/XRANGE,0,0.02TBPLOT,MKIN,1

3. The Multilinear Isotropic Hardening (MISO)

MPTEMP,1,0,500 ! Define temperature-dependent EX,

MP,EX,1,12E6,-8E3 ! as in above example

TB,MISO,1,2,5 ! Activate a data table

TBTEMP,0.0 ! Temperature = 0.0

TBPT,DEFI,3.67E-3,29.33E3 ! Strain, stress at temperature = 0

TBPT,DEFI,5E-3,50E3

TBPT,DEFI,7E-3,55E3

TBPT,DEFI,10E-3,60E3

TBPT,DEFI,15E-3,65E3

TBTEMP,500 ! Temperature = 500

TBPT,DEFI,3.67E-3,29.33E3 ! Strain, stress at temperature = 500

TBPT,DEFI,5E-3,37E3

TBPT,DEFI,7E-3,40.3E3

TBPT,DEFI,10E-3,43.7E3

TBPT,DEFI,15E-3,47E3

/XRANGE,0,0.02

TBPLOT,MISO,1

ТЕОРИЯ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ