Разработка математической модели кузова вагона
Лабораторная работа №1
Цель работы:
1. Разработка математической модели вертикальных колебаний кузова вагона на одноступенчатом рессорном подвешивании с гасителем колебаний сухого трения (сила зависит от загрузки вагона);
2. Исследование собственных и вынужденных колебаний, прогибов подвешивания, влияния жесткости подвешивания, коэффициента относительного трения, массы кузова на интенсивность колебаний.
Содержание работы:
1. Разработка математической модели кузова вагона с гасителем колебаний сухого трения;
2. Создание модели кузова вагона с рессорным подвешиванием в программном комплексе MEDYNA;
3. Анализ влияние жесткости подвешивания, коэффициента относительного трения, массы кузова на интенсивность собственных и вынужденных колебаний;
4. Формулирование выводов, их графическая иллюстрация;
5. Оформление отчета.
Введение
Плавное движение вагонов по пути с реальными неровностями обеспечивается благодаря системе рессорного подвешивания, состоящей из упругих элементов и гасителей колебаний. Рессоры обычно размещают между кузовом и колесными парами.
Возникающие при движении вагона в составе поезда динамические силы, отклонения от положения равновесия, инерционные перегрузки, которые действуют на пассажиров и грузы, являются следствием колебательных процессов и других видов неравномерного движения инерционных масс, составляющих рассматриваемую механическую систему.
Целью изучения колебаний вагона являются выяснение физической природы и причин, их вызывающих, установление допустимого уровня порождаемых ими динамических воздействий.
Нелинейное сопротивление демпферов в рессорах обычно применяется в грузовых вагонах, где оно осуществляется за счет работы сил сухого трения в клиновой системе.
Клиновой гаситель колебаний, имеющий силы трения, пропорциональные перемещениям, но различной величины для нисходящего и восходящего движений, применён практически во всех тележках грузовых вагонов. Силы трения в этих гасителях возникают при относительном вертикальном и горизонтальном перемещениях трущихся поверхностей.
Исходные данные
Исходные данные для моделирования колебаний кузова вагона в программном комплексе MEDYNA представлены в таблице 1.
Таблица 1 − Исходные данные для моделирования колебаний кузова вагона
| Параметр | Обозначение | Значение | |
| Масса кузова вагона, т | М | 14 (тара) | 90 (брутто) |
| Главный центральный момент инерции кузова для продольной оси, кг∙м2 | Ix | ||
| Главный центральный момент инерции кузова для поперечной оси, кг∙м2 | Iy | ||
| Главный центральный момент инерции кузова для вертикальной оси, кг∙м2 | Iz | ||
| Коэффициент относительного трения | φ | 0,4 | 0,15 |
| Жесткость одного рессорного комплекта, Н∙м-1 | Cz | 4∙106 | |
| Высота рессорного комплекта, м | h | 0,250 | |
| Продольное расстояние между центрами рессорных комплектов (база вагона), м | Lx | 8,650 | |
| Поперечное расстояние между центрами рессорных комплектов, м | Ly | 2,036 | |
| Высота центра масс кузова порожнего вагона над уровнем жесткого основания, м | Hт | 0,67 | |
| Высота центра масс кузова груженого вагона над уровнем жесткого основания, м | Hбр | 1,54 |
Динамическая модель вагона
Определение твердых тел и элементов связи
Для описания модели в MEDYNA необходимо выбрать твердые тела, которыми будет моделироваться вагон, задать их геометрию (положение центров масс тел и места крепления элементов связей — так называемых узлов), задать направления элементов связей (номера тел и принадлежащих им узлов, которые соединяются элементом связи). Далее модель конкретизируется заданием массовых характеристик тел (масс и моментов инерции), а также типов и параметров элементов связей.
В данной модели вагона выделяют одно твердое тело: кузов вагона. Схема вагона с обозначением номера тела и элементов связи изображена на рисунке 5.
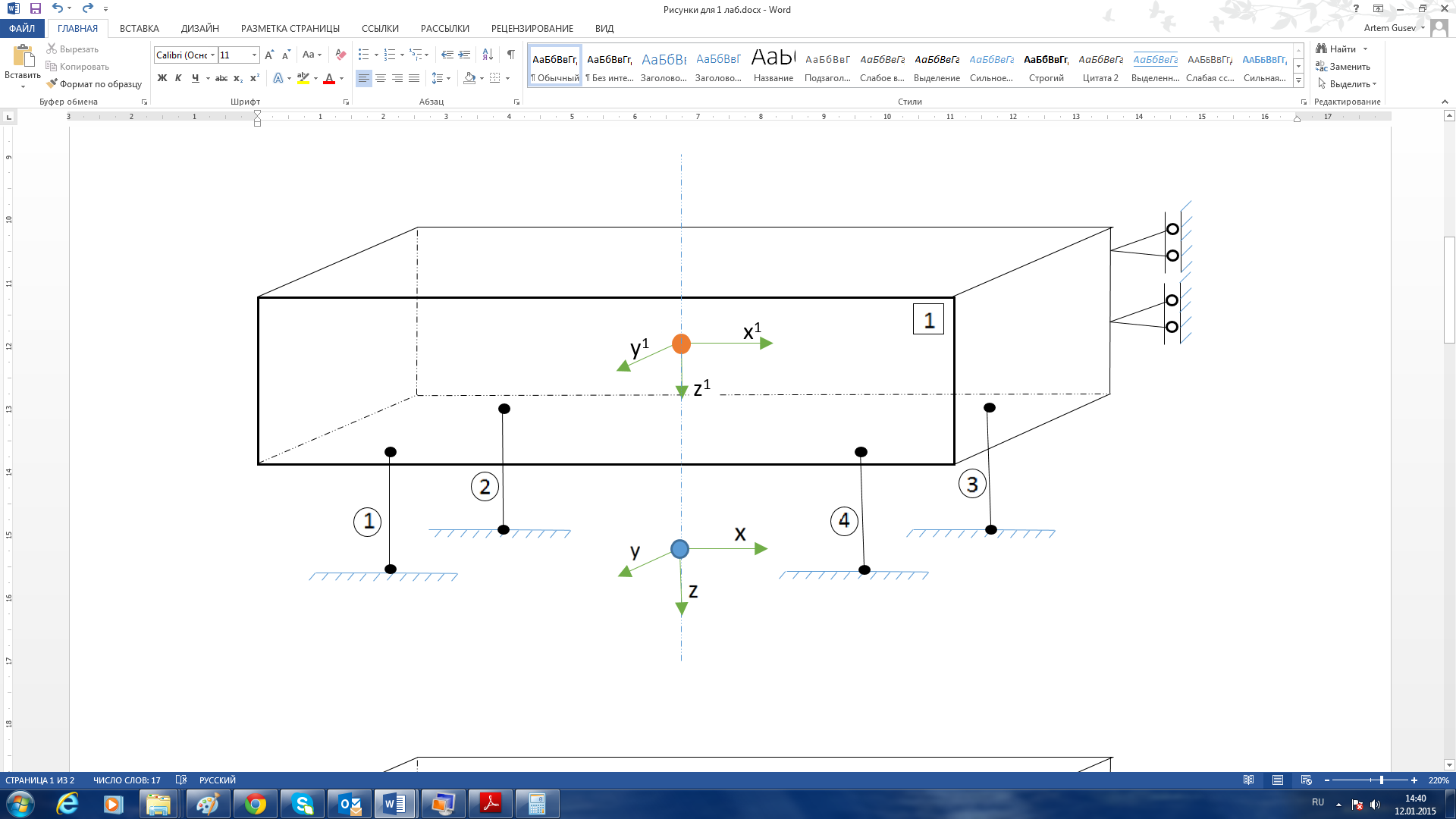
Рисунок 5 – Расчетная схема вагона с номерами тел (в прямоугольниках)
и элементами связи (в кружках)
Дальнейшее описание модели производится в том же порядке, что и ввод данных в блоках комплекса MEDYNA.
Задание геометрии многомассовой системы (блог KONFIG)
Первоначально в блоке KONFIG-MDEERD задается ускорение свободного падения, в блоке KONFIG-MDEREF - координаты узлов в отсчетной системе координат (значения и расположение представлены в таблице 2 и на рисунке 6).
Таблица 2 – Координаты узлов в отсчетной системе координат
| Номер узла | Название | Координаты, м | ||
| x | y | z | ||
| Жесткое основание №1 | -4,325 | 1,018 | ||
| Жесткое основание №2 | -4,325 | -1,018 | ||
| Жесткое основание №3 | 4,325 | -1,018 | ||
| Жесткое основание №4 | 4,325 | 1,018 |
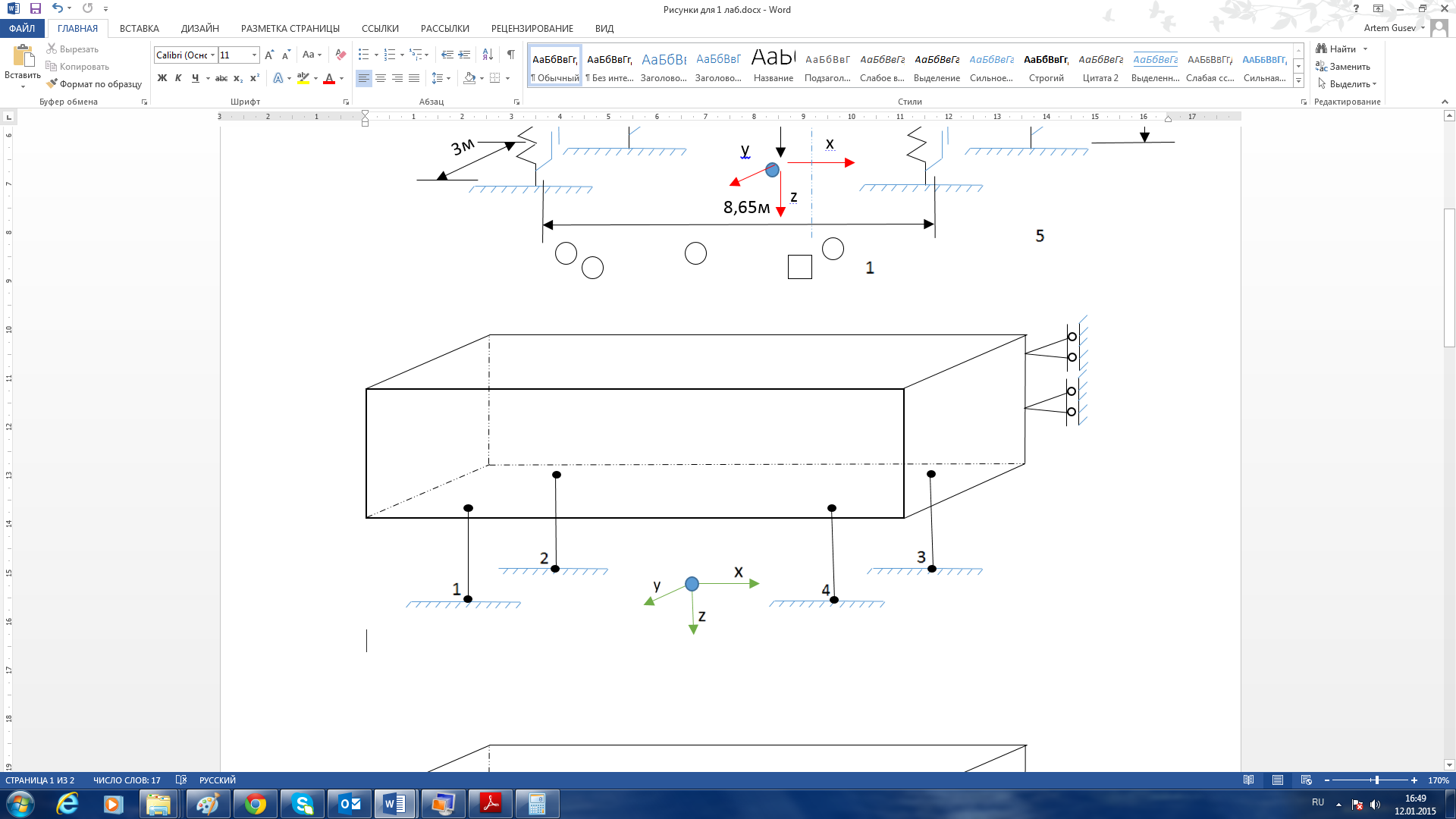
Рисунок 6 – Расположение узлов на жестком основании
Для конкретизации геометрии твердых тел для каждого из них задается своя, локальная, система координат (блог KONFIG-MDENOM). Ее ориентация (направление осей) обычно совпадает с ориентацией отсчетной системы координат, а положение начала отсчета располагается в центре масс тела (таблица 3).
Таблица 3 – Положение начала отсчета локальных систем координат тел модели относительно отсчетной системы координат
| Номер тела | Название | Координаты, м | |||
| x | y | z | |||
| тара | брутто | ||||
| Кузов вагона | -0,67 | -1,54 |
В блоке KONFIG-MDEAKO задают степени свобод тел (значения указаны в таблице 4), идентичность с другими телами модели, число узлов на каждом теле и номера узлов, расположенных в центре масс тел.
Таблица 4 – Название тел и соответствующие им степени свободы
| Номер тела | Название | Степени свободы* | |||||
| x | y | z | θ | φ | ψ | ||
| Кузов вагона |  | |  | | | | |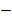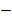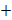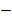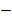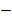
| _______________ * θ-угол боковой качки; φ-угол галопирования; ψ-угол виляния. |
Далее в локальных системах координат задают узлы, определяющие места крепления элементов связи (блок KONFIG-MDEKNI). Число, название и координаты узлов тела представлены в таблице и на рисунке 7.
Таблица 5 – Координаты узлов на кузове вагона
| Номер узла | Название | Координаты, м | |||
| x | y | z | |||
| тара | брутто | ||||
| Центр масс | |||||
| Подвешивание №1 | -4,325 | 1,018 | 0,42 | 1,29 | |
| Подвешивание №2 | -4,325 | -1,018 | 0,42 | 1,29 | |
| Подвешивание №3 | 4,325 | -1,018 | 0,42 | 1,29 | |
| Подвешивание №4 | 4,325 | 1,018 | 0,42 | 1,29 |
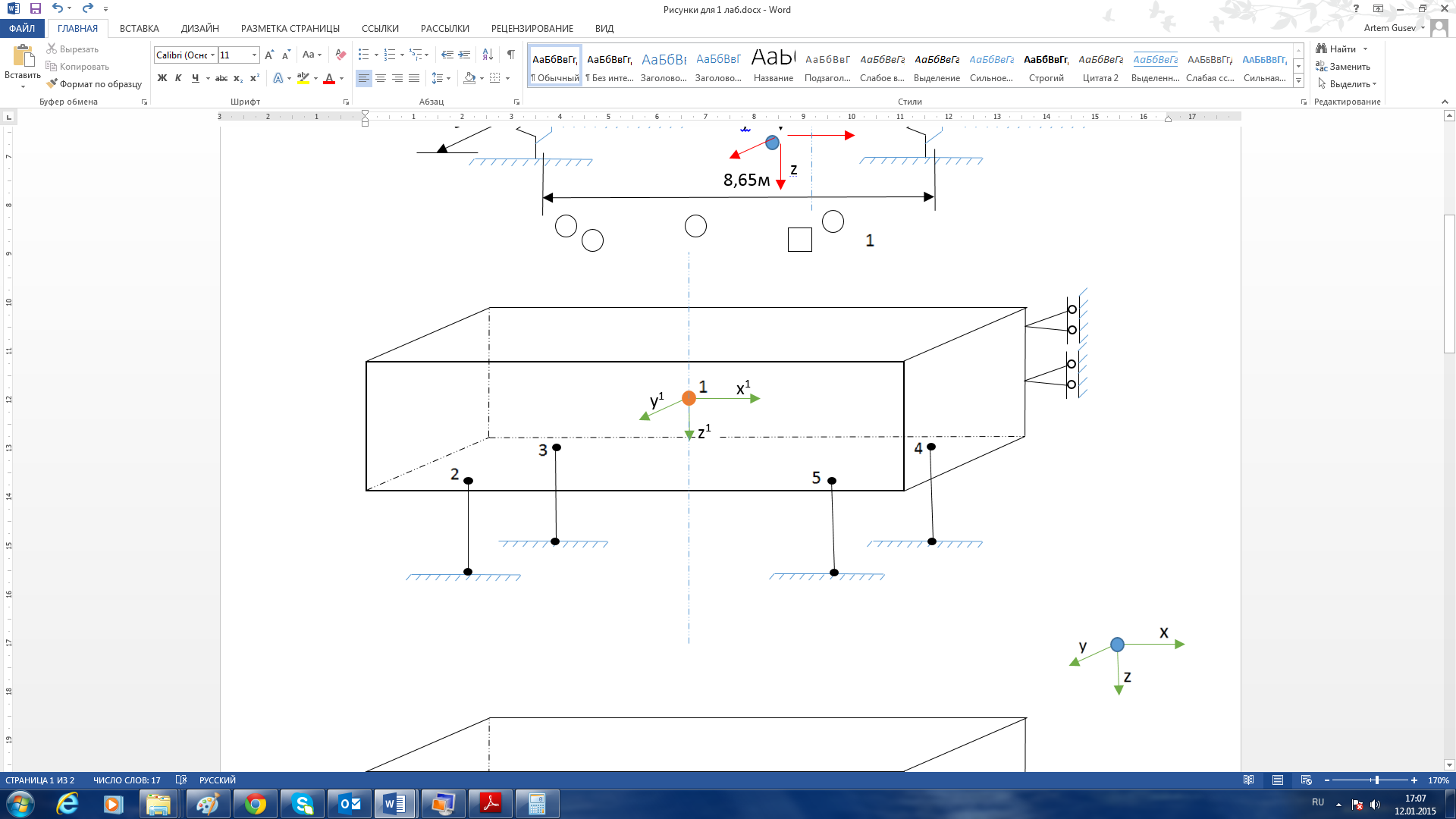
Рисунок 7 – Расположение узлов на кузове вагона
В блоке KONFIG-MDESKM задаются массы и массовые моменты инерции тела. Инерционные параметры для вагона представлены в исходных данных (таблица 1). Указываем массу порожнего вагона и соответствующие данной загрузке инерционные характеристики.
После завершения ввода инерционных параметров тел в блоке
KONFIG-MDESKM автоматически выполнится блок KONFIG-MDETEP, в котором описываются степени свободы тел многомассовой системы относительно связанных с телами исходных систем координат (рисунок 8).
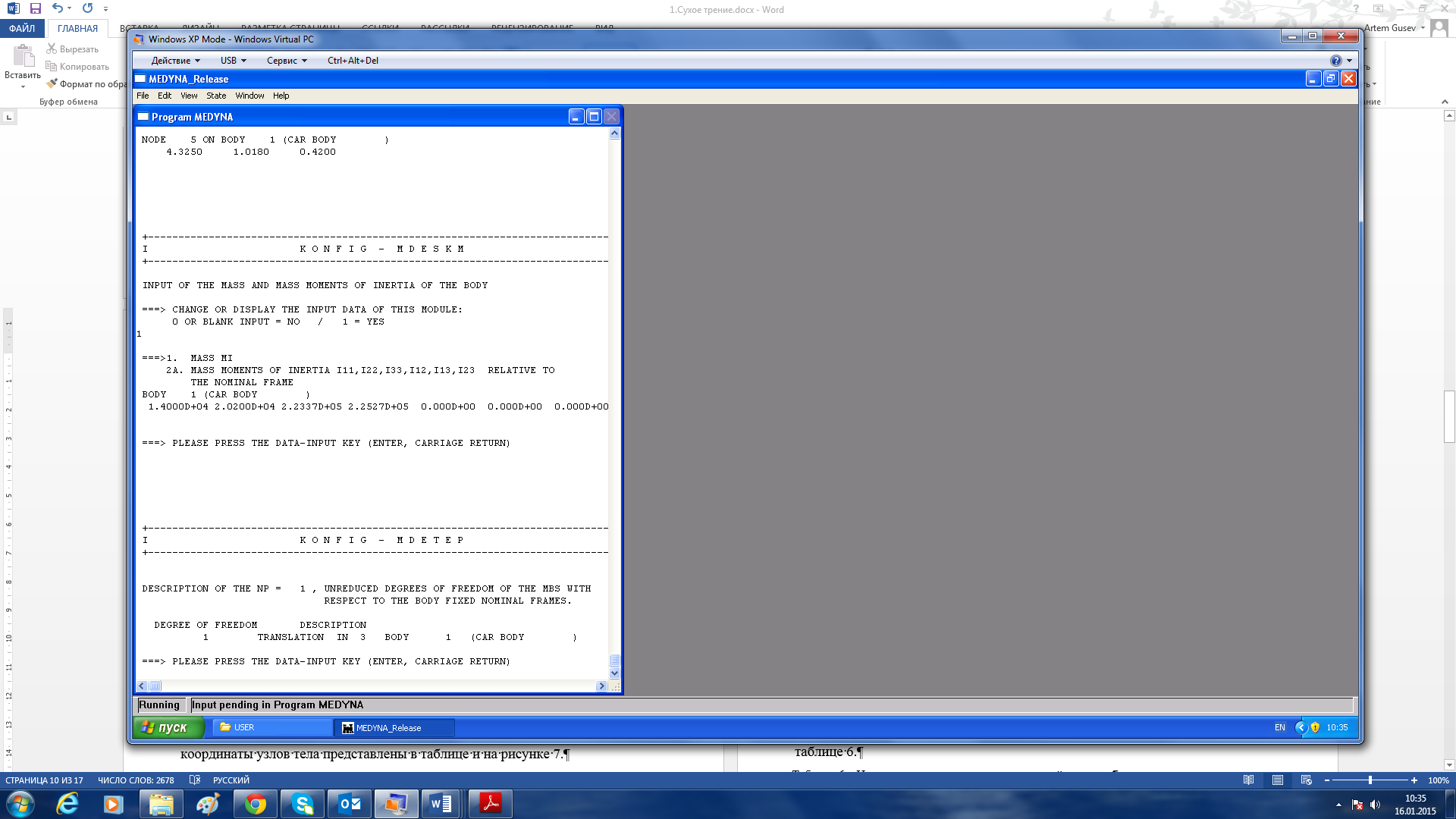
Рисунок 8 – Описание степеней свободы тел в блоке KONFIG-MDETEP
Задание связей и их параметров для описания взаимодействия тел (блок VERBIN)
Для задания связей в твердотельной модели указывают их направления, которые определяются номерами узлов связываемых тел (блок VERBIN-MDEBIN). Для связей, обладающих схожими характеристиками, можно задать их идентичность, чтобы избежать повторного ввода параметров. Номера, названия, направления и идентичность связей (в соответствии с нумерацией, принятой в MEDYNA) для вагона на одноступенчатом рессорном подвешивании отражены в таблице 6.
Таблица 6 – Номера, названия и направления связей в модели
| Номер связи | Название | Тело i | Тело j | Идентичность | ||
| Номер тела | Номер узла | Номер тела | Номер узла | |||
| Подвешивание №1 | ||||||
| Подвешивание №2 | ||||||
| Подвешивание №3 | ||||||
| Подвешивание №4 |
По окончании блока VERBIN-MDEBIN программой автоматически генерируются таблица исходных векторов зазоров в связях (таблица 7), для каждой связи выводится модуль и направление вектора перемещения (блок VERBIN-MNOMRE).
Таблица 7 – Модули и направления векторов перемещения в связях
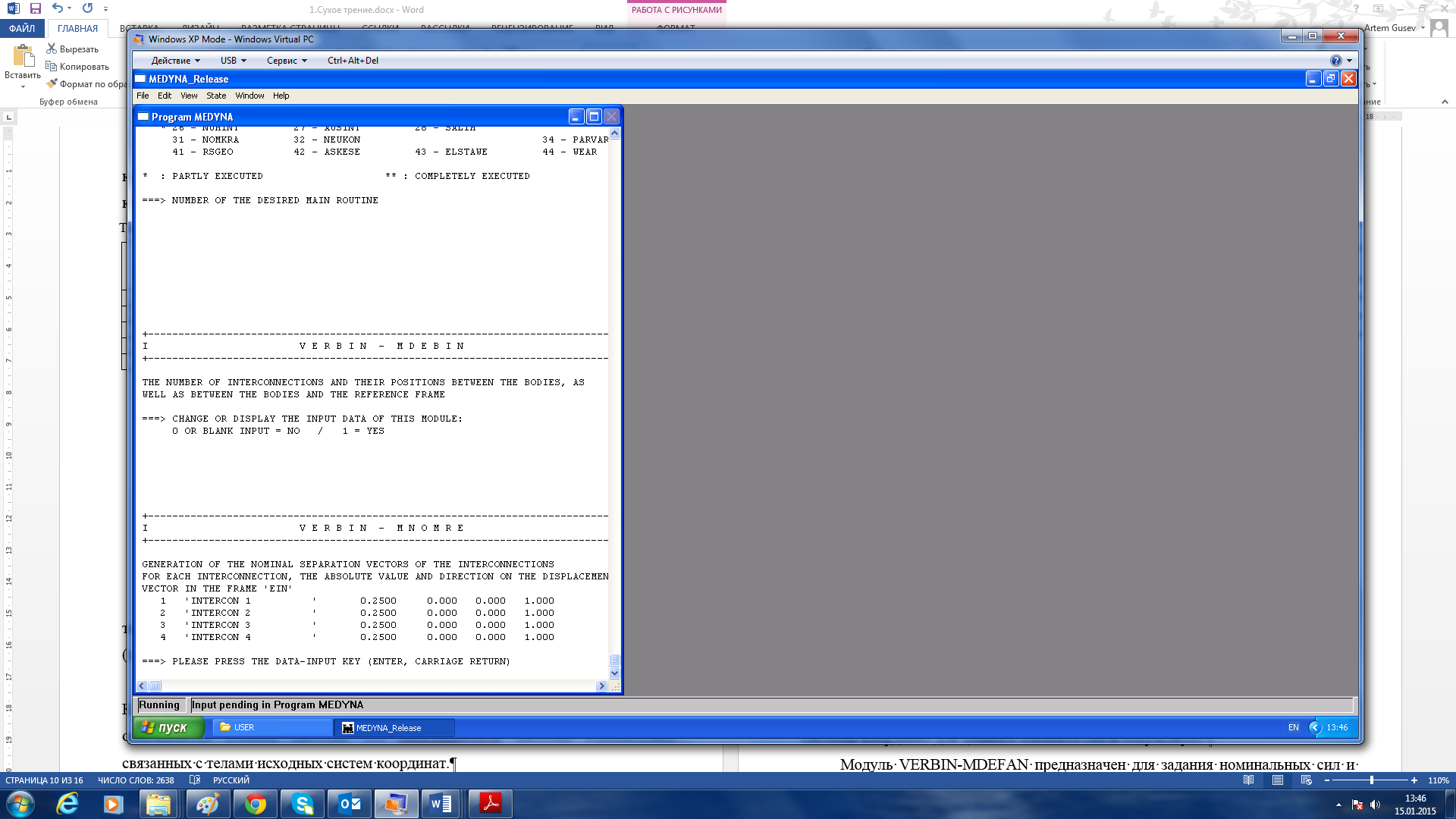
Далее в блоке VERBIN-MDEKET задаются типы элементов связей и их параметры. В данном случае нелинейный элемент №296. Опция задания ориентации вспомогательной системы координат для данного элемента связи отсутствует.
Модуль VERBIN-MDEFAN предназначен для задания номинальных сил и моментов в связях. В данной модели вертикальных колебаний кузова вагона модуль VERBIN-MDEFAN не используется, поэтому его пропускаем.
В модуле VERBIN-MDEK 296 задаются параметры элементов связи. Фактор положения условной точки на длине связи указываем 0,5. Обозначаем координатные оси, по которым действуют силовые факторы (вертикальная ось):
0 0 1
Жесткость для одного рессорного подвешивания указываем равной 4 МН, что соответствует исходным данным (таблица 1). В модуле VERBIN-MDEK 296 указываем характеристики рессорного подвешивания в таком же порядке, в каком описан элемент №296 в пункте 4.
Параметры 1-6:
4.е6 100.е6 0.4 2. 3. 3.
Параметры 7-10:
2. 1.001 0. 0.0
Задание входных возмущений в телах, связях (блог ANREG)
Чтобы система пришла в движение, начала колебаться, необходимо внешнее воздействие. Для анализа собственных колебаний, внешнее воздействие осуществляется в виде единичного силового импульса, по результатам которого происходят затухающие колебания. Для анализа вынужденных колебаний, внешнее воздействие осуществляется в виде периодически повторяющегося силового импульса (синусоидальное возмущение). Окно модуля ANREG изображено на рисунке 9.
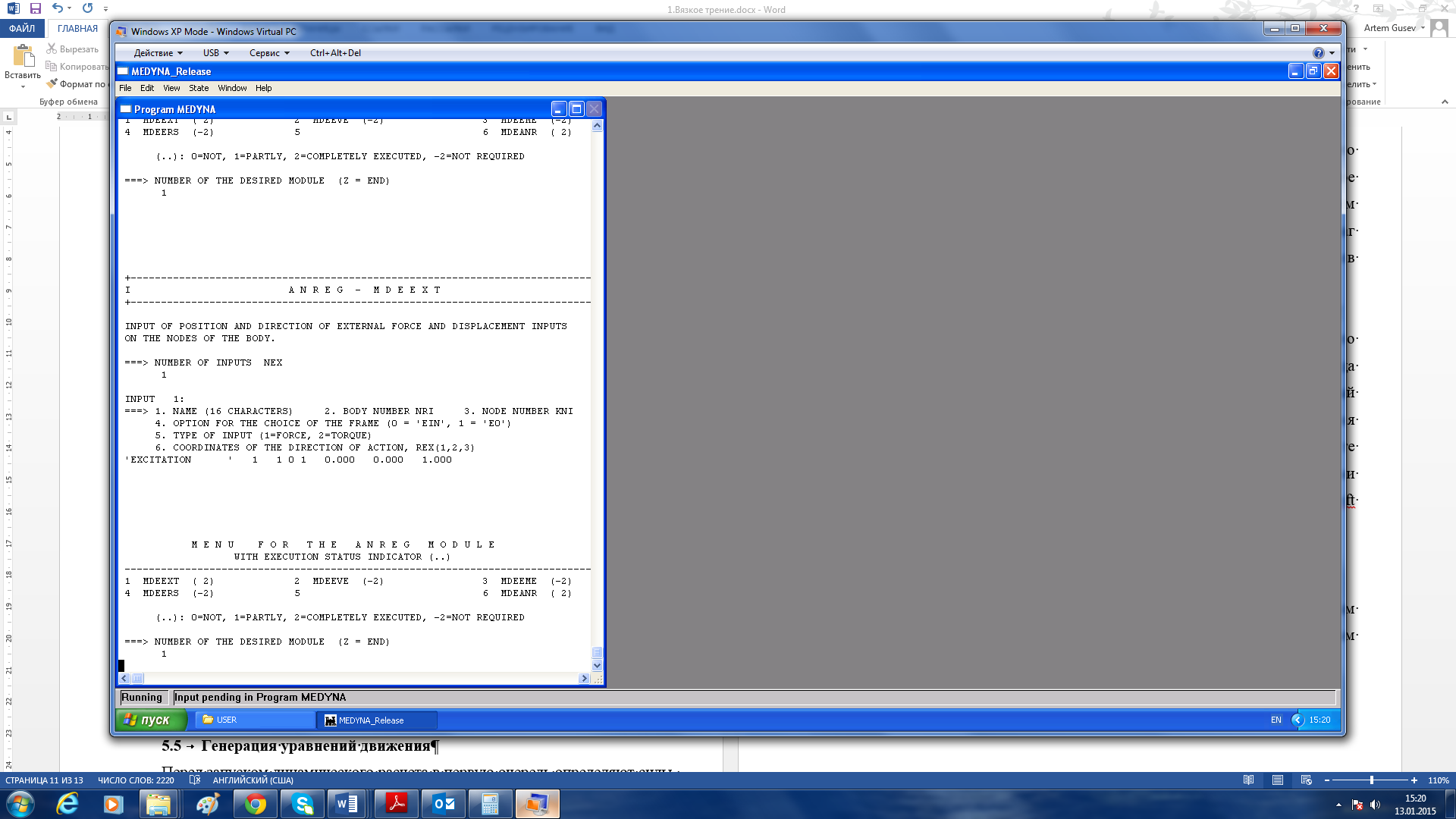
Рисунок 9 – Модуль ANREG
В разделе ANREG-MDEEXT указывается вид возмущения (сила или момент), к каким узлам оно прикладывается и в каком направлении действует возмущение. Ввод данных производится в следующей последовательности:
1. Имя (16 символов) 2. Номер тела 3. Номер узла
4. Опция выбора системы координат (0=локальная, 1=отсчетная)
5.Тип воздействия (1=сила, 2=момент)
6. Выбор координатных осей, по которым направлено воздействие
‘Excitation’ 1 1 0 1 0.0 0.0 1.0
В разделе ANREG-MDEANR выбираются типы возмущений:
1. Имя (16 символов) 2. Постоянный вход (только силы и моменты)
3. Тип возмущения
0=нет 1=гармоническое 2=функция спектральной плотности
3=цветной шум (формирующий фильтр) 4=функция времени
5=функция расстояния
‘Free oscillations’ 0.0 4
Затем необходимо выбрать из выпадающего списка («-1»=вывести список всех существующих функций) номер возмущающей функции. Для моделирования свободных колебаний выбираем прямоугольный импульс (№3), функция которого
U(T)=0. для T<A2 и T>A3
U(T)=A1 иначе
А1=300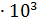 
Н, А2=2 сек, А3=2,1 сек.
Вводим данные в следующем порядке:
300.e3 2. 2.1
Графическое представление прямоугольного импульса изображено на рисунке 10.
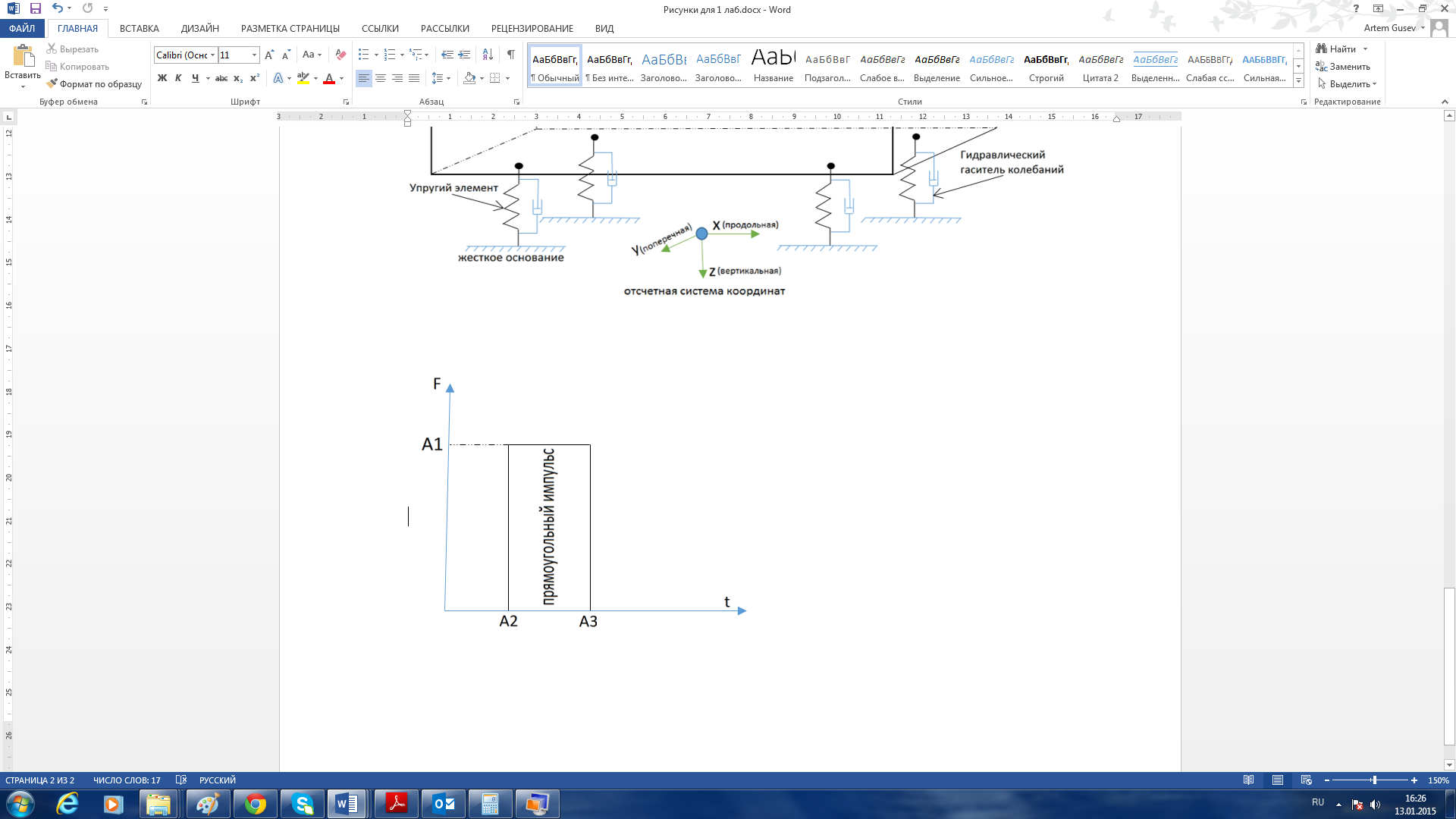
Рисунок 10 – Прямоугольный импульс
Для моделирования вынужденных колебаний выбираем синусоидальное возмущение (№1), функция которого
U(T)=A1*SIN(A2*T+A3),
где А1=300 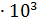Н – амплитуда колебаний; А2=ω=2π=6,28 рад/сек– круговая (циклическая) частота; А3=0 – начальная фаза колебаний.
Вводим данные в следующем порядке:
300.e3 6.28 0.
Примеры получения результатов собственных и вынужденных колебаний из динамической модели программного комплекса MEDYNA
График свободных колебаний кузова порожнего вагона, полученный при выведении системы из состояния покоя силовым импульсом величиной A1=300 кН, представлен на рисунке 11.
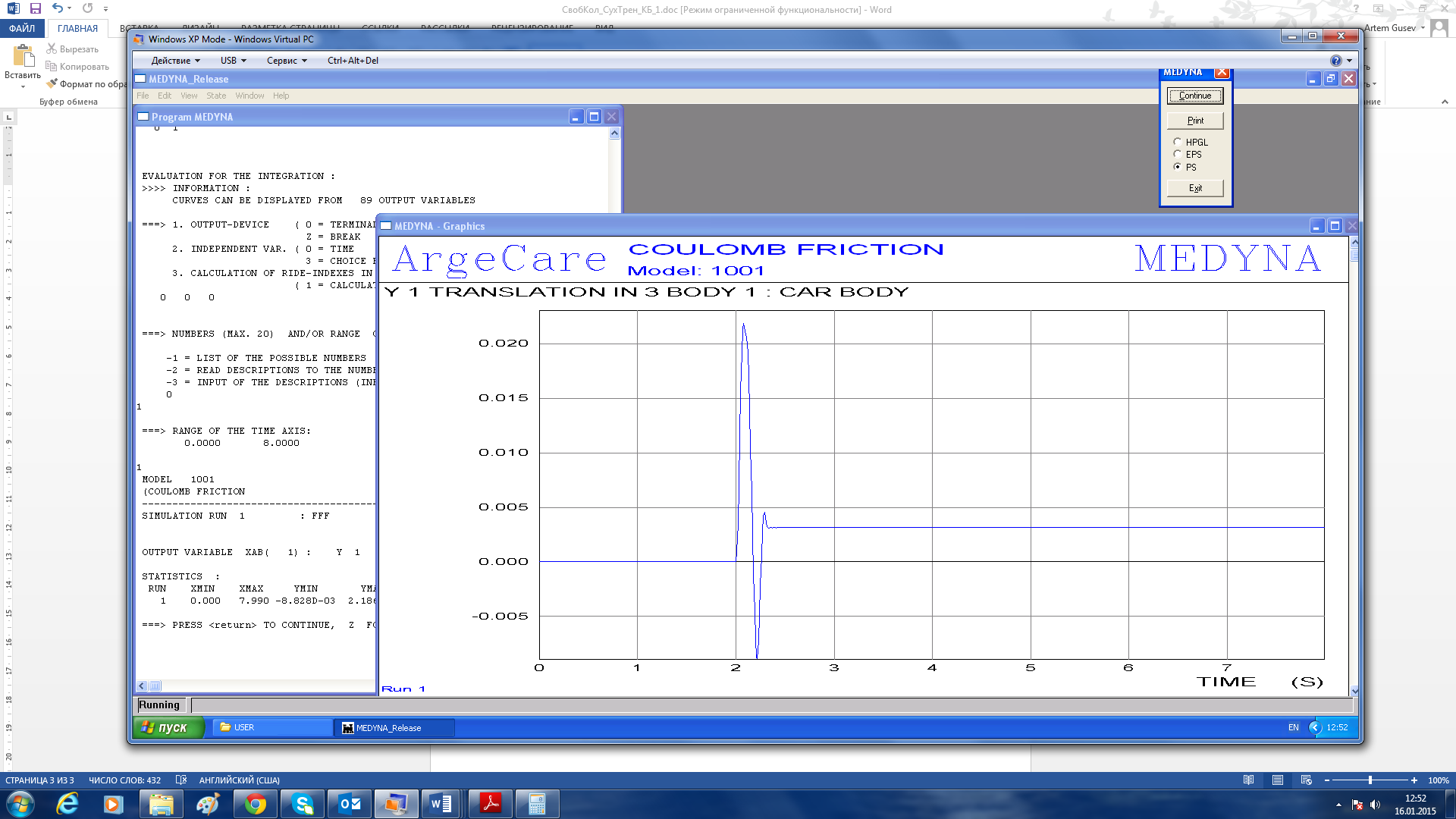
Рисунок 11 – График собственных колебаний кузова порожнего вагона
За четверть периода кузов будет находиться в точке находящейся от положения равновесия на расстоянии +а или –а (рисунок 12).
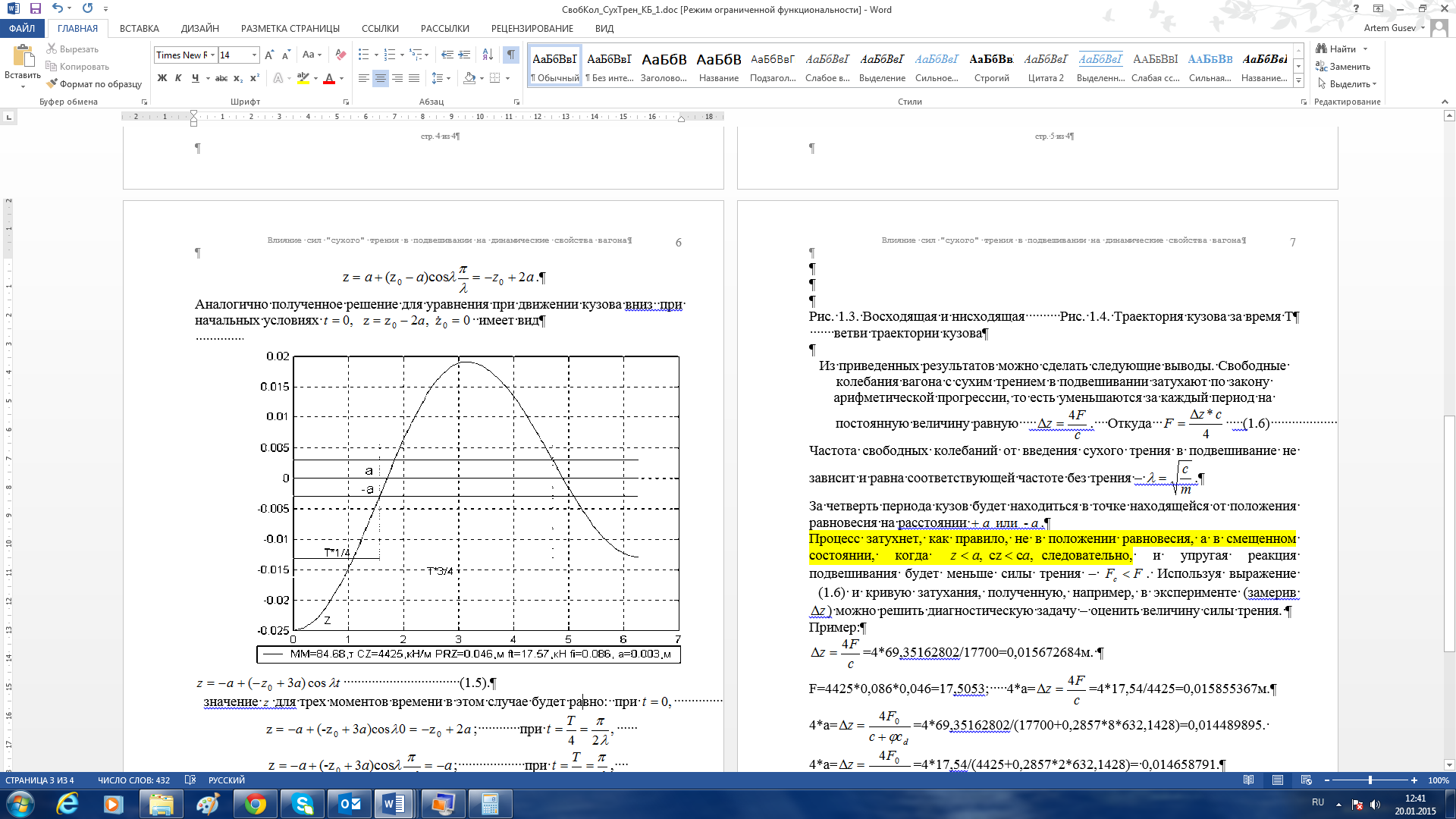
Рисунок 12 – Восходящая и нисходящая ветви траектории кузова
Процесс свободных колебаний затухнет, как правило, не в положении равновесия, а в смещенном состоянии, когда 
, 
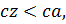следовательно, и упругая реакция подвешивания будет меньше силы трения – Fc<F.
График вынужденных колебаний кузова порожнего вагона, полученный при наложении на систему синусоидального импульса величиной A1=300 кН с циклической частотой ω=6,28 рад/сек представлен на рисунке 13.
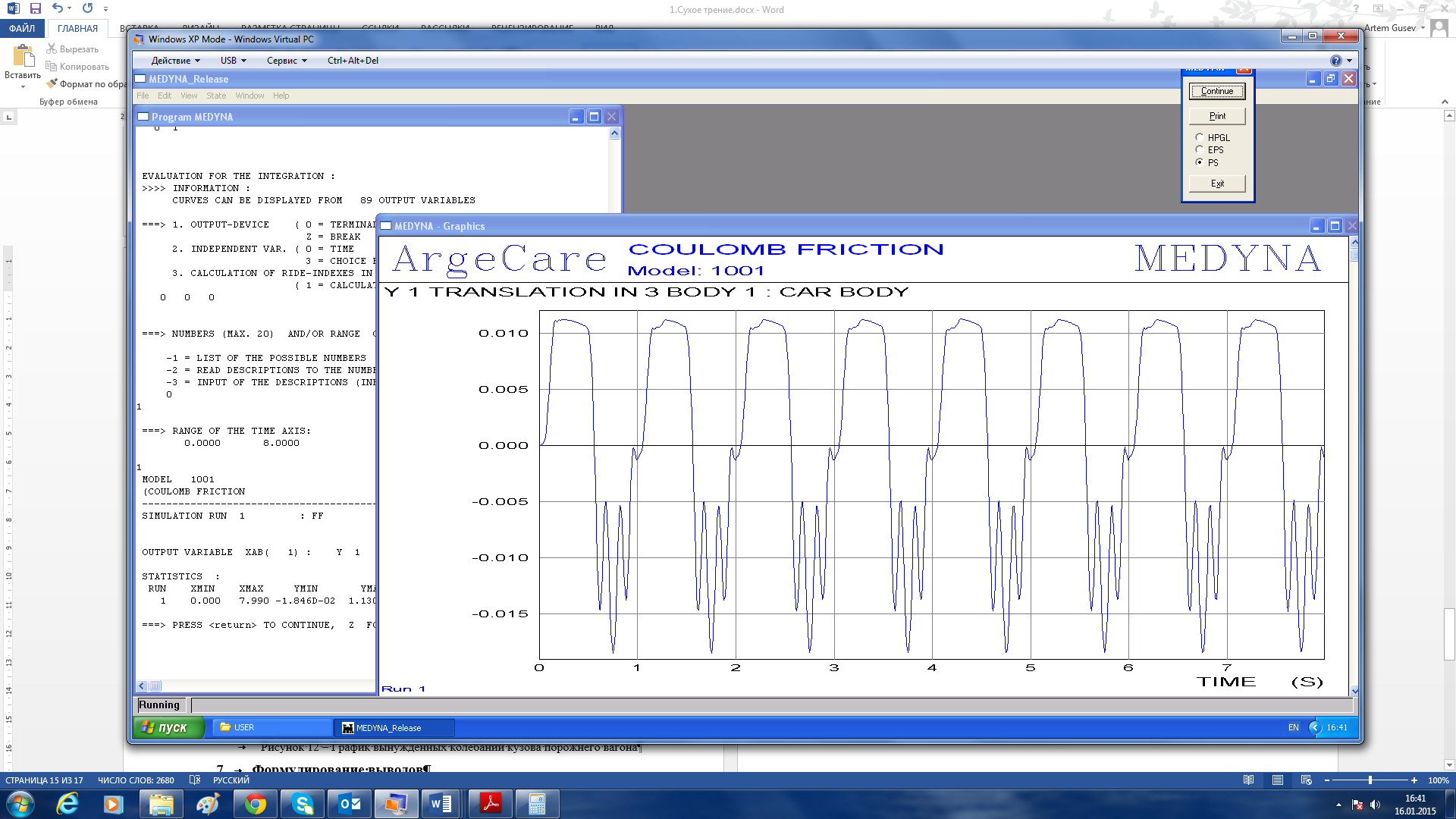
Рисунок 13 – График вынужденных колебаний кузова порожнего вагона
Формулирование выводов
Проанализировать влияния жесткости подвешивания, коэффициента относительного трения гасителя колебаний и загруженности вагона на собственные и вынужденные колебания кузова, (данные для анализа представлены в таблицах 8-11). Дополнительно произвести оценку влияния циклической частоты вынужденных колебаний ω на характер колебательного процесса.
Обратить внимание на прогибы подвешивания. Привести в выводах графики колебаний кузова вагона, полученные в программном комплексе MEDYNA.
Таблица 8 – Изменение жесткости подвешивания
| № | Жесткость подвешивания, МН/м | Коэффициент относительного трения |
| от 1 до 3 | от 1 до 5 | 0,4 |
Таблица 9 – Изменение коэффициента относительного трения
| № | Жесткость подвешивания, МН/м | Коэффициент вязкого трения, кг/сек |
| от 1 до 3 | от 0,15 до 0,4 |
Таблица 10 – Влияние загруженности вагона на колебательный процесс
| № | Жесткость подвешивания, МН/м | Коэффициент относительного трения | Силовой импульс, кН | |
| от 1 до 3 | Mт=14т | Mбр=90т | от 700 до 1400 | |
| 0,4 | 0,15 |
Таблица 11 – Изменение циклической частоты
| № | Жесткость подвешивания, МН/м | Коэффициент относительного трения | Циклическая частота, рад/сек |
| от 1 до 3 | от 1 до 5 | 0,4 | от π до 4π |
Лабораторная работа №1
Цель работы:
1. Разработка математической модели вертикальных колебаний кузова вагона на одноступенчатом рессорном подвешивании с гасителем колебаний сухого трения (сила зависит от загрузки вагона);
2. Исследование собственных и вынужденных колебаний, прогибов подвешивания, влияния жесткости подвешивания, коэффициента относительного трения, массы кузова на интенсивность колебаний.
Содержание работы:
1. Разработка математической модели кузова вагона с гасителем колебаний сухого трения;
2. Создание модели кузова вагона с рессорным подвешиванием в программном комплексе MEDYNA;
3. Анализ влияние жесткости подвешивания, коэффициента относительного трения, массы кузова на интенсивность собственных и вынужденных колебаний;
4. Формулирование выводов, их графическая иллюстрация;
5. Оформление отчета.
Введение
Плавное движение вагонов по пути с реальными неровностями обеспечивается благодаря системе рессорного подвешивания, состоящей из упругих элементов и гасителей колебаний. Рессоры обычно размещают между кузовом и колесными парами.
Возникающие при движении вагона в составе поезда динамические силы, отклонения от положения равновесия, инерционные перегрузки, которые действуют на пассажиров и грузы, являются следствием колебательных процессов и других видов неравномерного движения инерционных масс, составляющих рассматриваемую механическую систему.
Целью изучения колебаний вагона являются выяснение физической природы и причин, их вызывающих, установление допустимого уровня порождаемых ими динамических воздействий.
Нелинейное сопротивление демпферов в рессорах обычно применяется в грузовых вагонах, где оно осуществляется за счет работы сил сухого трения в клиновой системе.
Клиновой гаситель колебаний, имеющий силы трения, пропорциональные перемещениям, но различной величины для нисходящего и восходящего движений, применён практически во всех тележках грузовых вагонов. Силы трения в этих гасителях возникают при относительном вертикальном и горизонтальном перемещениях трущихся поверхностей.
Исходные данные
Исходные данные для моделирования колебаний кузова вагона в программном комплексе MEDYNA представлены в таблице 1.
Таблица 1 − Исходные данные для моделирования колебаний кузова вагона
| Параметр | Обозначение | Значение | |
| Масса кузова вагона, т | М | 14 (тара) | 90 (брутто) |
| Главный центральный момент инерции кузова для продольной оси, кг∙м2 | Ix | ||
| Главный центральный момент инерции кузова для поперечной оси, кг∙м2 | Iy | ||
| Главный центральный момент инерции кузова для вертикальной оси, кг∙м2 | Iz | ||
| Коэффициент относительного трения | φ | 0,4 | 0,15 |
| Жесткость одного рессорного комплекта, Н∙м-1 | Cz | 4∙106 | |
| Высота рессорного комплекта, м | h | 0,250 | |
| Продольное расстояние между центрами рессорных комплектов (база вагона), м | Lx | 8,650 | |
| Поперечное расстояние между центрами рессорных комплектов, м | Ly | 2,036 | |
| Высота центра масс кузова порожнего вагона над уровнем жесткого основания, м | Hт | 0,67 | |
| Высота центра масс кузова груженого вагона над уровнем жесткого основания, м | Hбр | 1,54 |
Разработка математической модели кузова вагона
В данной работе рассматривается случай колебания кузова вагона, рессорное подвешивание которого представлено упругими элементами с гасителями колебаний сухого трения. При разработке модели принимают, что отсчетная система координат (тело «0») находится на жестком основании в центре продольной и поперечной симметрий вагона. Тела, моделирующие вагон, совершают колебания относительно отсчетной системы координат. Ось Х отсчетной системы координат направлена вдоль оси пути по направлению движения вагона, ось Y – перпендикулярно вправо, ось Z – перпендикулярно вниз.
Необходимо обратить внимание на то, что в программном комплексе MEDYNA обозначение системы координат (x, y, z) заменено на эквивалентное цифровое (1, 2, 3).
Математическая модель кузова вагона представлена на рисунке 1.
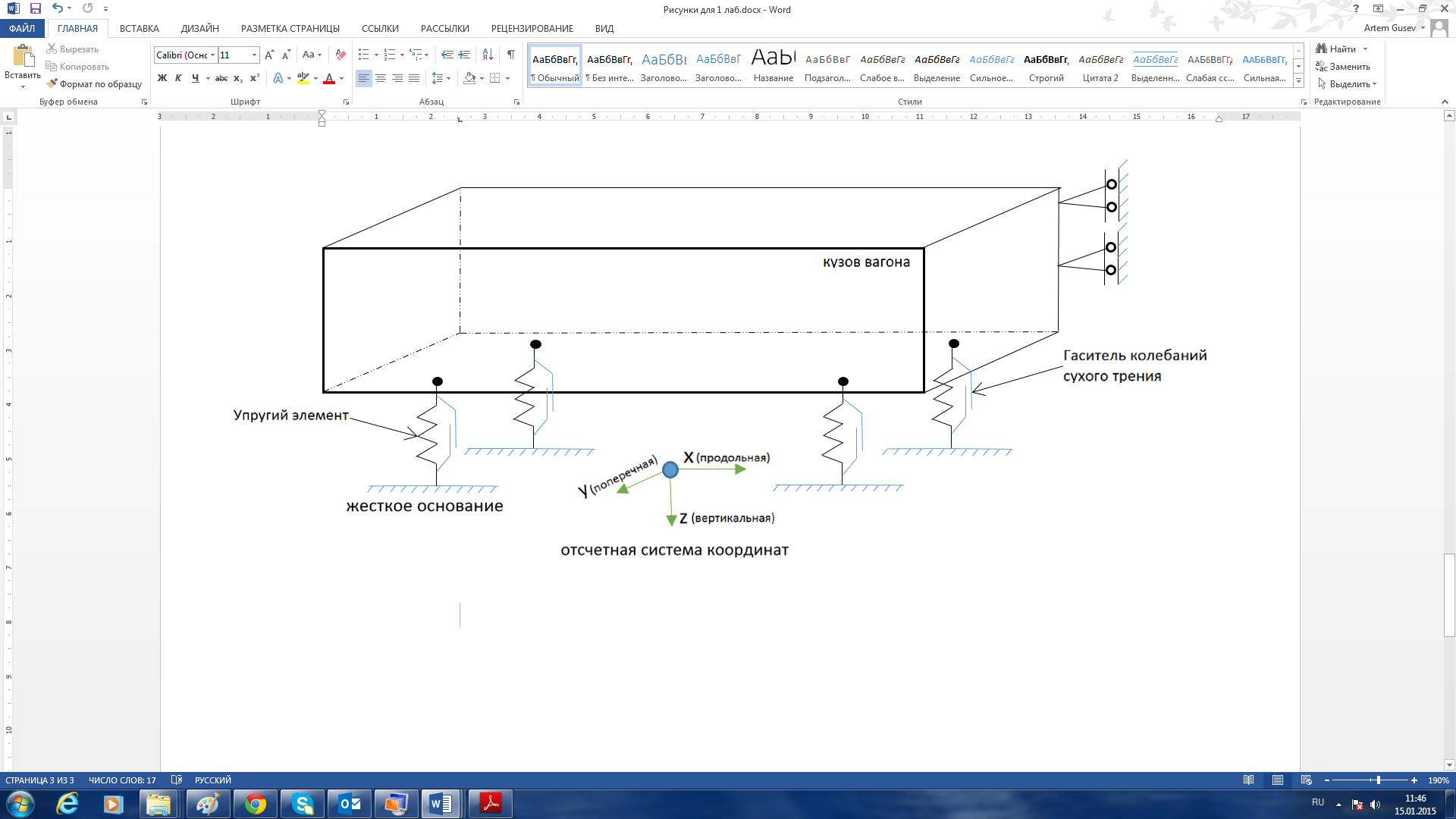
Рисунок 1 – Математическая модель кузова вагона на рессорном подвешивании с гасителями колебаний сухого трения
Для конкретизации геометрии твердых тел (в данном случае одно тело – кузов вагона) для каждого из них задается своя, локальная (x1, y1, z1), система координат. Ее ориентация (направление осей) обычно совпадает с ориентацией отсчетной системы координат, а положение начала отсчета располагается в центре масс тела.
Математическая модель кузова вагона с геометрическими параметрами и обозначением отсчетной и локальной систем координат представлена на рисунке 2.
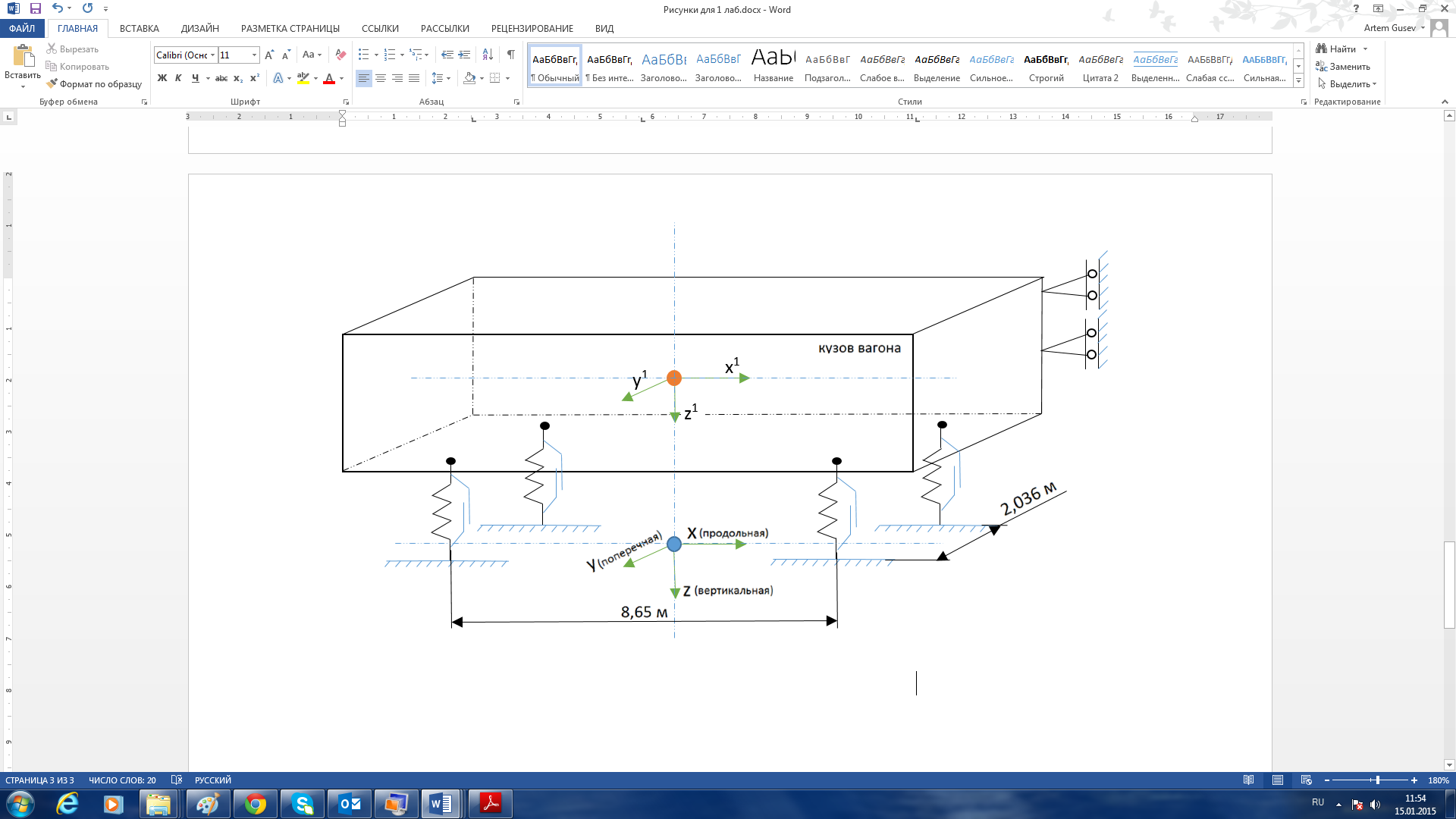
Рисунок 2 – Геометрические параметры математической модели
Так как в работе рассматривается модель вертикальных колебаний кузова, то на перемещения в продольном и поперечном направлениях, а также на повороты относительно любых осей накладываются ограничения.