Лекция 20. матричная форма метода перемещений

МАТРИЦА ЖЕСТКОСТИ СТЕРЖНЯ

Предположим, что нужно рассчитать некоторую произвольную пространственную стержневую систему, изображенную на рис. 20.1.

Расчет будем вести методом перемещений с учетом всех видов деформаций стержня: растяжения-сжатия, кручения и изгиба. В качестве основных неизвестных примем узловые перемещения и повороты. При принятых предпосылках в каждом узле будет 3 линейных и 3 угловых перемещения. Будем определять эти перемещения в некоторой общей для всей конструкции системе координат XYZ, называемой в дальнейшем глобальной системой координат. Общее число неизвестных равно, таким образом, 6×N , где N — число узлов конструкции. Если у конструкции имеются опорные связи, число которых равно С₀, то соответствующие им перемещения равны нулю, и число неизвестных уменьшится на С₀. Следовательно, общее число неизвестных n равно 6×N – С₀.

Рис.20.1. Произвольная пространственная стержневая система

Рассмотрим реализацию метода, считая (для простоты выводов), что внешние силы приложены только в узлах конструкции. Пролетные нагрузки всегда можно привести к узловым силам, так что введенное ограничение не является принципиальным.

Вырежем i-й узел конструкции (см. рис.20.2).

Рис.20.2. Узел i

Уравнения равновесия i-го узла имеют вид:

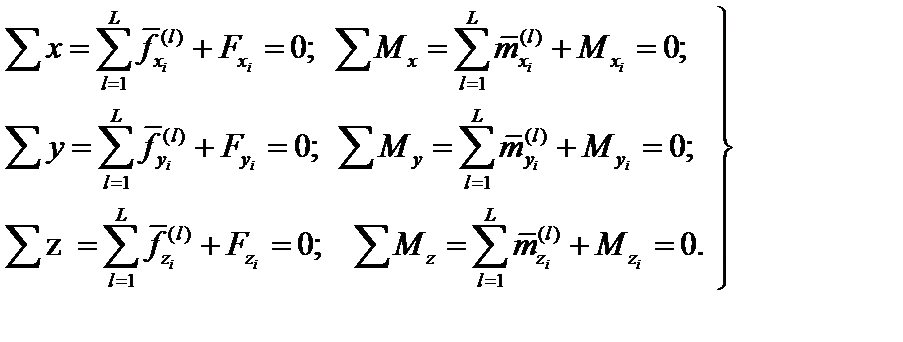(20.1)

Суммирование усилий проводится по всем стержням, сходящимся в данном узле. Номера этих стержней меняются от 1 до L. Уравнения (20.1) в матричном виде записываются так:

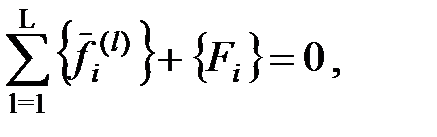(20.2)

где:

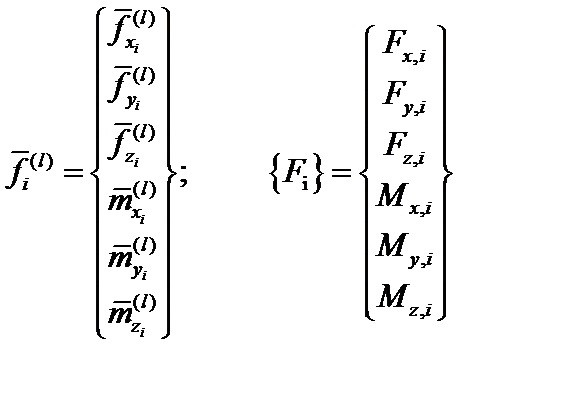(20.3)

Вектор 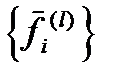содержит проекции концевых сил стержня i-j на координатные оси XYZ. Сразу найти эти проекции по формулам сопротивления материалов не представляется возможным. Можно, однако, найти концевые силы в местной системе координат x_m y_m z_m , которая выбирается следующим образом: ось x_mнаправляется вдоль оси стержня, а оси y_mи z_m совмещаются с главными осями инерции поперечного сечения. Местная система координат для стержняi-j показана на рис. 20.1. На рис.20.3 и 20.4 показаны положительные направления для концевых усилий и перемещений стержня в местной системе координат. В отличие от сопротивления материалов, принято единое правило знаков для i-го и j-го концов стержня.

Рис.20.3. Усилия и перемещения в плоскости x_m – y_m

Рис.20.3. Усилия и перемещения в плоскости z_m – y_m

С учетом введенного правила знаков для усилий и перемещений зависимость между ними в местной системе координат (МСК) на основании таблицы сил и моментов 16.1 для однопролетной статически неопределимой балки (см. раздел 4 лекции 16) можно представить в виде одной матричной формулы:

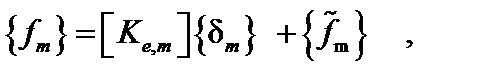(20.4)

где

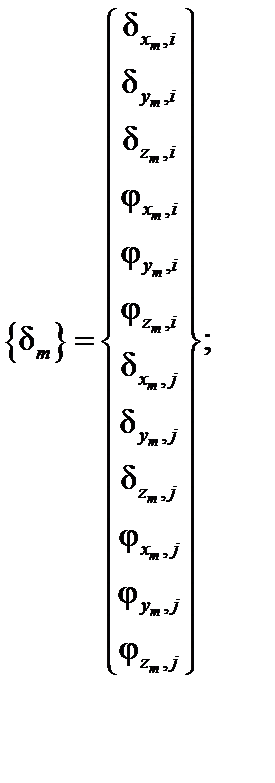(20.5)

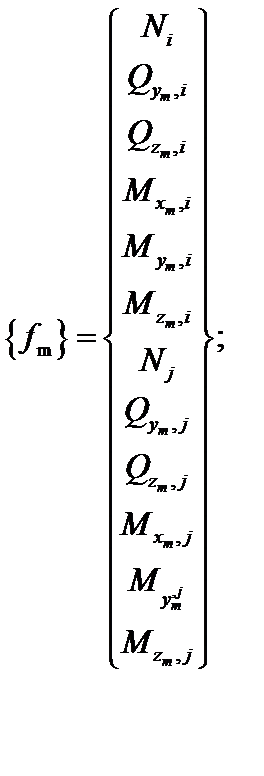(20.6)

(20.7)

а вектор 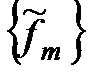состоит из двенадцати компонентов узловых сил, обусловленных пролетными нагрузками. Эти компоненты могут быть найдены в зависимости от вида пролетной нагрузки из таблиц эпюр моментов и поперечных сил для однопролетных балок.