Канонические уравнения метода сил

Методику расчета стержневых конструкций методом сил рассмотрим на примере.

Пример.

Пусть требуется рассчитать раму, изображенную на рис. 13.8.

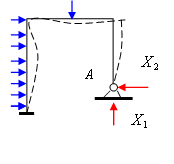
Рис.13.8. Рассчитываемая рама

На рисунке показана схема рамы, опорные закрепления и внешние нагрузки. Реакции на правой опоре обозначены как Х₁ и Х₂. Рама является статически неопределимой, т.к. количество неизвестных опорных реакций, равное 5, превышает число уравнений статики, равное 3, на 2. Следовательно, рама дважды статически неопределима. Чтобы решить задачу, примем в качестве основных неизвестных усилия в лишних связях и перейдем от расчета заданной конструкции к расчету основной системы. Основная система образуется из заданной конструкции путем удаления лишних связей. Различные варианты основной системы показаны на рис. 13.9. Каждая из них получена удалением двух связей.Для дальнейшего расчета примем основную систему, показанную на рис. 13.9,а.

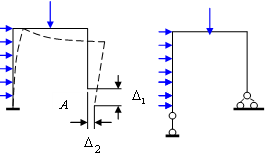
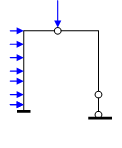
а б в

Рис.13.9. Различные варианты основной системы: а – отброшены две связи на правой опоре, б – отброшены две связи и на левой опоре, в - отброшена одна связь на правой опоре и врезан шарнир

Отметим, что основная система, показанная на рис. 13.9,а, отличается от заданной конструкции как в силовом, так и в кинематическом отношениях. Силовое отличие заключается в том, что в заданной конструкции на правой опоре возникают опорные реакции Х₁ и Х₂, в основной же системе в точке А нет опор и, следовательно, нет и никаких сил. Кинематическое отличие состоит в том, что в заданной конструкции на опоре А нет перемещений, в основной же системе точка А может перемещаться как по горизонтали, так и по вертикали. Чтобы сделать основную систему эквивалентной заданной конструкции, приложим в точке А силы Х₁ и Х₂, устранив таким образом силовое несоответствие, и потребуем, чтобы перемещения по направлению отброшенных связей были равны нулю, что приведет к устранению кинематического несоответствия. Эквивалентная система показана на рис. 13.10.

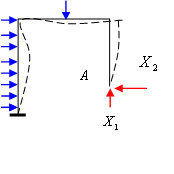
Рис.13.10. Эквивалентная система

Условия равенства нулю перемещений по направлению отброшенных связей можно записать в следующем виде:

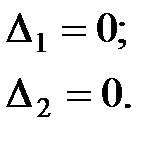(13.2)

Перемещения в основной системе вызываются внешними силами, а также силами Х₁ и Х₂. Воспользовавшись принципом суперпозиции, соотношения (13.2) запишем в виде:

,

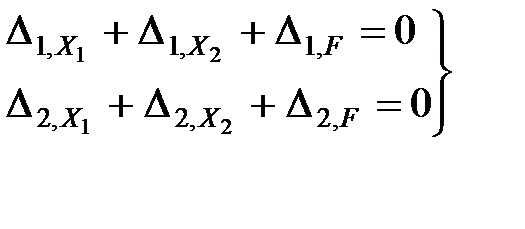(13.3)

где 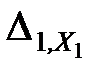— перемещение по направлению первой отброшенной связи от действия силы Х₁;

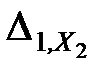— перемещение по направлению первой отброшенной связи от действия силы Х₂;

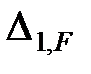— перемещение по направлению первой отброшенной силы от внешних сил и т.д.

Перемещения от сил Х₁и Х₂можно представить следующим образом:

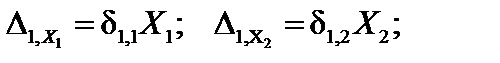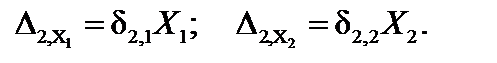(13.4)

В формулах (13.4) δ_1,1 — перемещение в направлении первой отброшенной связи от силы Х₁ =1; δ_1,2 — перемещение в направлении первой отброшенной связи от силыХ₂ =1 и т.д.

Подставляя формулы (13.4) в уравнения (13.3), получаем систему из двух уравнений с двумя неизвестными:

.

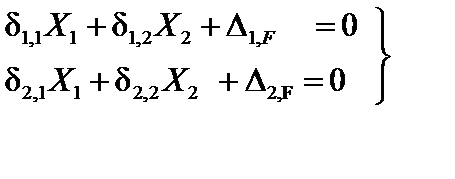(13.5)

Полученные уравнения называются каноническими уравнениями метода сил. В случае конструкции с n неизвестными канонические уравнения метода сил имеют следующий вид:

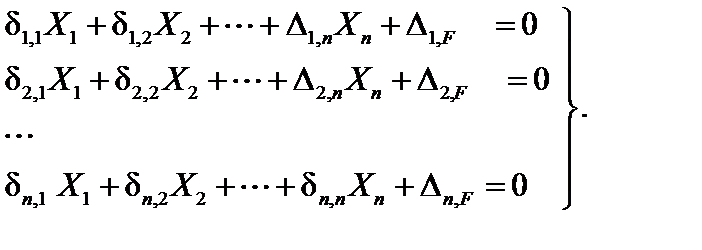(13.6)

Коэффициенты канонических уравнений представляют собой перемещения в основной системе. Их можно найти по формуле Мора, а именно:

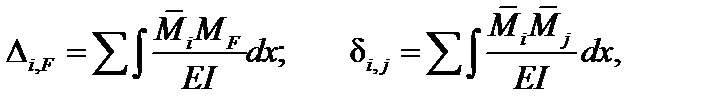
где 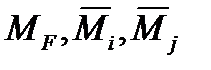- моменты в основной системе от нагрузки и сил 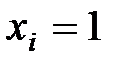и 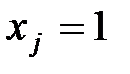соответственно.

Интегралы, входящие в формулу Мора, можно найти по способу Верещагина или по методу Симпсона. Таким образом, для определения коэффициентов канонических уравнений необходимо построить эпюры изгибающих моментов для основной системы от заданной нагрузки и от единичных значений неизвестных. После вычисления коэффициентов и решения системы канонических уравнений окончательная эпюра изгибающих моментов для заданной конструкции может быть построена по формуле:

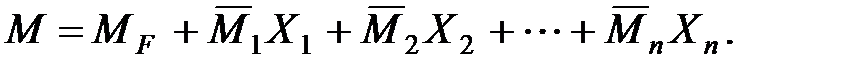
Эпюра поперечных сил может быть построена по эпюре изгибающих моментов с использованием известных из курса сопротивления материалов дифференциальных зависимостей между изгибающим моментом и поперечной силой. Эта зависимость имеет следующий вид:

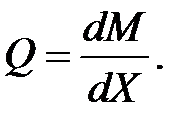
Эпюра продольных сил может быть построена с использованием эпюры поперечных сил и способа сечений. Для проверки правильности построения окончательной эпюры изгибающих моментов можно использовать то обстоятельство, что перемещения по направлению отброшенных связей должны быть равны нулю. Математически это условие выражается так:

.

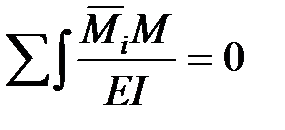С учетом изложенного выше, алгоритм расчета конструкций методом силможно сформулировать следующим образом:

● подсчитать число лишних связей;

●выбрать основную систему;

● составить канонические уравнения метода сил;

●определить коэффициенты канонических уравнений;

● решить систему канонических уравнений;

● построить окончательные эпюры моментов;

● построить эпюры поперечных сил;

● построить эпюру продольных сил;

● проверить правильность построения окончательной эпюры моментов.

ЛЕКЦИЯ 14. ПРИМЕРЫ РАСЧЕТА РАМ МЕТОДОМ СИЛ