Лекция 8.определение перемещений в арках и фермах

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В АРКАХ

Пример. Найти прогиб ключевого сечения арки, изображенной на рис.8.1 при:

Рис.8.1. К определению перемещений в арке

Очертание оси арки — окружность. Радиус R окружности,по которой очерчена арка определяется по формуле:

,

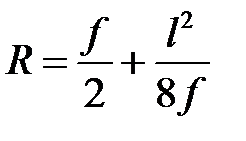Уравнение оси:

;

Функции угла наклона касательной:

.

Решение. Прогиб найдем по формуле Мора с учетом только изгибающих моментов. Эта формула в данном случае принимает вид:

гдеds - элемент дуги арки. Остальные величины в формуле Мора имеют прежний смысл. При постоянной изгибной жесткости формула Мора приводится к виду:

Если учесть, что (см.рис.8.1), формула принимает вид:

Особенность расчета арок заключается в том, что обе эпюры моментов — и грузовая, и единичная, — являются криволинейными. Поэтому способ Верещагина вычисления интеграла оказывается неприемлемым, а из численных способов предпочтительнее использовать способ трапеций. Способ трапеций заключается в том, что интервал интегрирования разбивается на участки, желательно одинаковой длины, и на каждом участке площадь подынтегральной кривой находится как площадь трапеции. Желательно, чтобы на каждом участке подынтегральная кривая была гладкой.

Разобьем пролет арки на восемь равных частей длиной Ввиду того, что на участках 2-4 и 6-8 характер нагрузки меняется, каждый из этих участков разобьем на две части, как показано на рис.8.1. Границы участков пронумеруем цифрами от 0 до 10. Номера участков будем определять по номеру правого на данном участке сечения. При использовании способа трапеций вычисления нужно вести по формуле:

Изгибающие моменты от нагрузкибудем искать по формуле:

(см. лекцию №3),

где балочные изгибающие моменты и распор арки от нагрузки. Аналогичным образом могут быть найдены изгибающие моменты от единичной силы, т.е.:

где балочные моменты и распор арки от единичной силы.

В свою очередь, для определения балочных значений необходимо предварительно найти вертикальные опорные реакции. Для рассматриваемой арки вертикальные реакции от нагрузки были найдены в примере 1 из лекции 3. Они равны ,

Чтобы найти реакции от единичной силы, нагрузим арку, как показано на рис.8.2.

Рис.8.2. Нагружение арки единичной силой

Очевидно, что = =0,5 (сила Р - безразмерная). Горизонтальную реакцию от единичной силы найдем из уравнения:

Дальнейшие расчеты проводим в табличной форме (см. табл.1).

Значение суммы элементов последнего столбца дает значение выражения из формулы (*).

Значение прогиба найдем, разделив это значение на изгибную жесткость. Получаем:

Таблица 1. Вычисление прогиба центральной точки

Номер сечения	Номер участка	X, м	У,м		Δx, м	МР, КНм	(м)
	-			0,3425					-
			6,25	0,7096		-44,1	-2,46	152,9	305,8
			9,2	0,8828		-42,5	-2,57	123,7	553,2
		11,2	10,5	0,9595	3,2	-56,6	-1,9	112,1	352,5
			10,7	0,9720	0,8	-21,3	-1,64	35,9	59,1
			11,2						71,8
			10,7	0,9720		37,5	-1,64	-63,3	-126,6
		22,4	9,95	0,9267	2,4	66,13	-2,3	-164	-272,8
			9,2	0,8828	1,6	80,67	-2,57	-234,8	-319
			6,25	0,7096		65,5	-2,46	-227,1	-923,8
				0,3425					-454,2

Σ=-754 кНм³