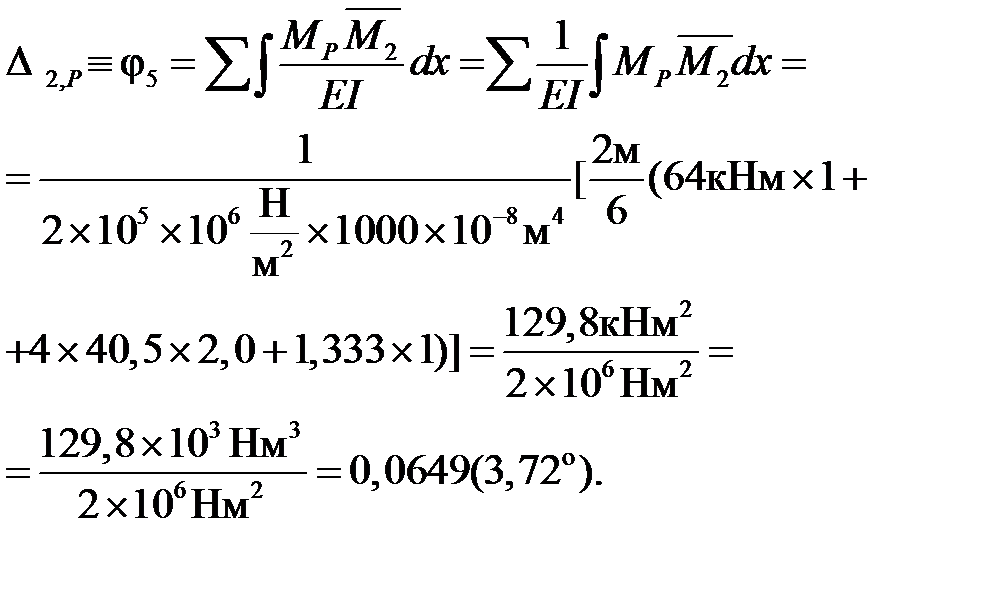Определение перемещений от смещения опор

Предположим, что в статически определимой балке одна из опор, например, правая, сместилась вниз на расстояние D (рис.6.9). Предположим, что при этом

а б

Рис.6.9. К определению перемещений от смещения опор: а – заданное воздействие, б – действие единичной силы

на опорах балки возникли опорные реакции. Составим уравнения равновесия балки:

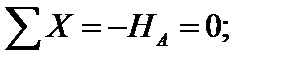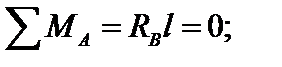
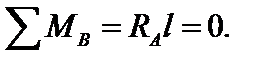
Из уравнений равновесия вытекает, что опорные реакции в статически определимой балке при смещении опоры равны нулю. Для определения перемещений точек воспользуемся принципом возможных перемещений.

Рассмотрим единичное состояние, в котором к конструкции приложена единичная сила в направлении искомого перемещения. Рассматривая это состояние как действительное, а состояние конструкции при смещении опоры как возможное, запишем уравнение принципа возможных перемещений:

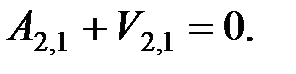(6.23)

Работа А_2,1 внешних сил единичного состояния на перемещениях заданного состояния равна:

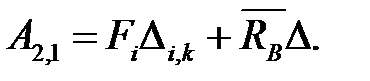(6.24)

Работа V_2,1 внутренних сил единичного состояния на перемещениях заданного равна нулю, т.к. деформации в статически определимой системе при смещении опор равны нулю. Заметим, что перемещения и деформации есть разные понятия: перемещение связано с точкой, а деформация — с отрезком. Из уравнений (6.23) и (6.24) получаем:

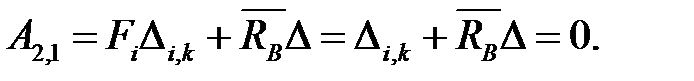(6.25)

В уравнении (6.25) учтено, что сила F_i=1.

Исходя из изложенного выше, можно сформулировать следующие правила вычисления перемещений, вызванных смещением опор:

1) приложить единичную силу, считая смещающуюся опору неподвижной;

2) определить реакции в тех опорных связях, которые в действительном состоянии смещаются;

3) составить выражение для работы внешних сил единичного состояния на перемещениях действительного и приравнять его нулю;

4) из полученного уравнения найти искомое перемещение.

При смещении нескольких опор формула (6.25) принимает вид:

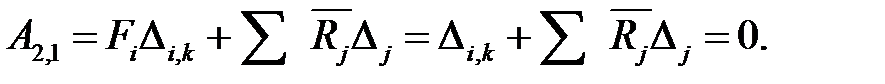
Отсюда:

(6.26)

ЛЕКЦИЯ 7. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ

В СТЕРЖНЕВЫХ СИСТЕМАХ

Пример 1. Найти прогиб в сечении 4 и угол поворота в сечении 2 составной балки (рис.7.1,а) при следующих исходных данных:

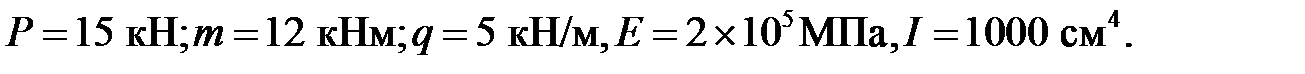
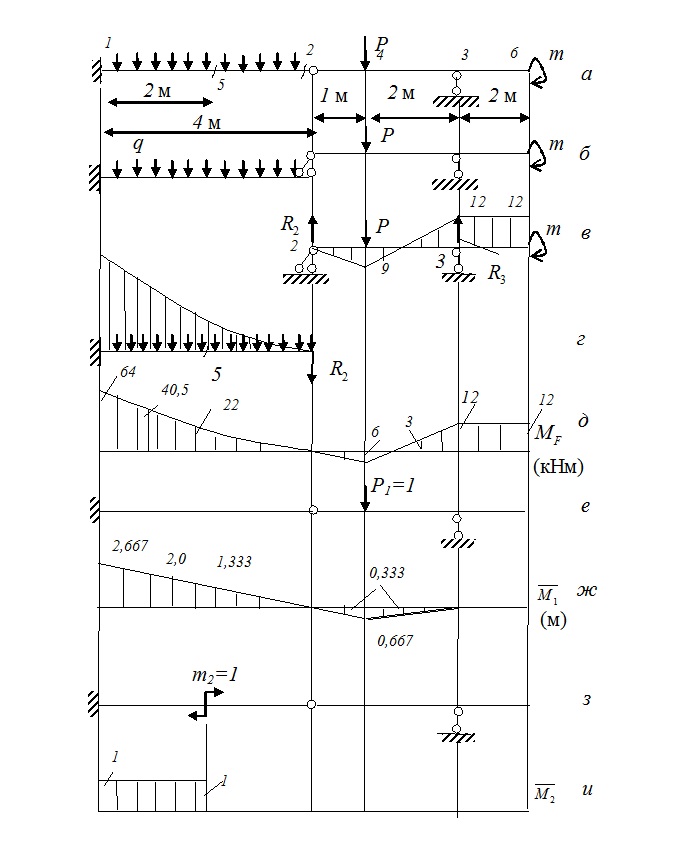
Рис.7.1. К примеру 1

Решение.

1. Построение грузовой эпюры моментов

1.1) Строим поэтажную схему (см. рис.7.1,б).

1.2) Проводим расчет вспомогательной балки 2-3 (рис.7.1,в).

Определение опорных реакций:

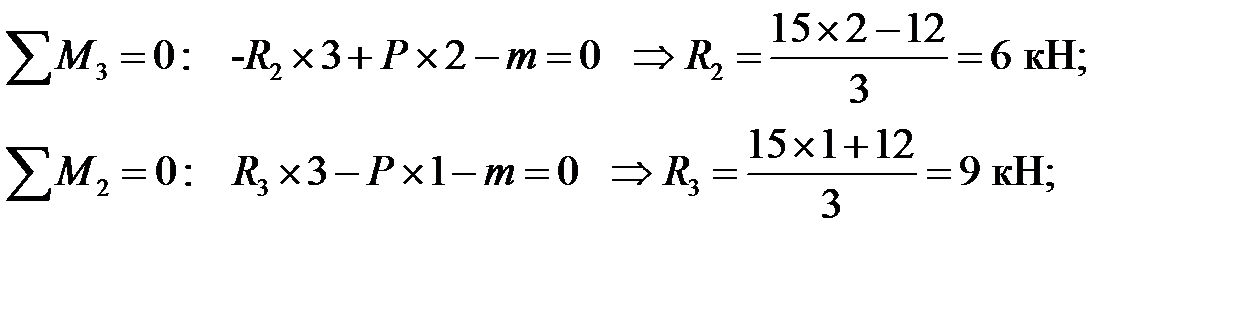
Проверка: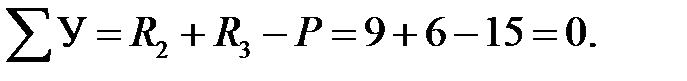

Определение изгибающих моментов:

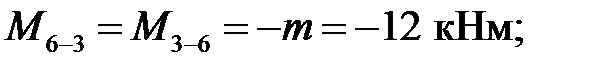
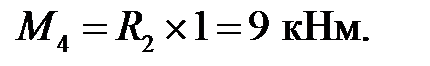
Cхема вспомогательной балки и эпюра изгибающих моментов для нее приведены на рис.7.1,в.

1.3) Рассчитываем главную балку 1-2.

Консольную балку можно рассчитать, не определяя опорных реакций. Находим изгибающие моменты:

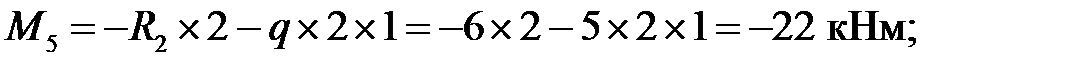
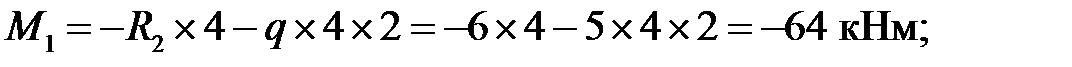
Cхема главной балки и эпюра изгибающих моментов для нее приведены на рис.7.1,г.

1.4) Объединяем эпюры изгибающих моментов, построенные для каждой балки в отдельности, и получаем грузовую эпюру изгибающих моментов для составной конструкции.

2. Для определения прогиба в точке 4 приложим в этой точке единичную силу, как показано на рис.7.1,е, и построим эпюру изгибающих моментов 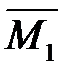от этой силы (см. рис.7.1,ж; промежуточные расчеты опущены).

3. Находим прогиб по формуле Мора (используем формулу численного интегрирования Симпсона):

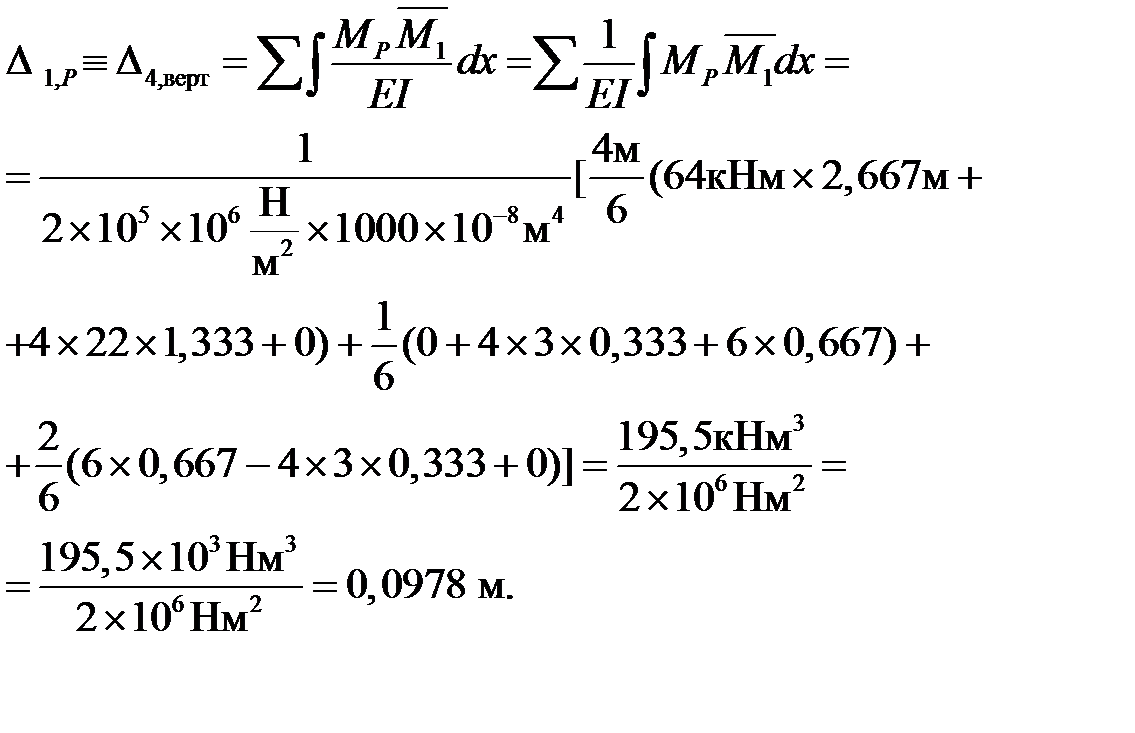
4. Для определения угла поворота сечения 5 прикладываем в этом сечении единичный момент (рис.7.1,з) и строим эпюру изгибающих моментов 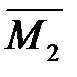от этого воздействия (рис.7.1,и).

5. По формуле Мора находим угол поворота: