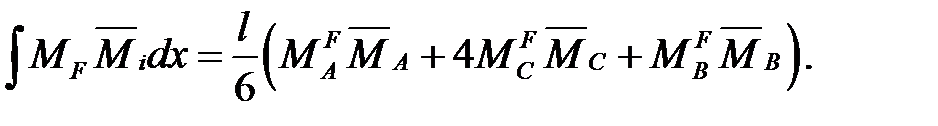Определение перемещений в стержневых системах от силового воздействия
Пусть на некоторую стержневую систему (см.рис.6.1) действует произвольная нагрузка. Внутренние силы, соответствующие этому состоянию, обозначим индексом F. Таким образом, на элемент конструкции длиной ds в этом состоянии действуют внутренние силы 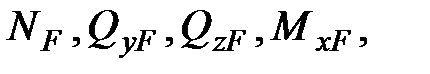
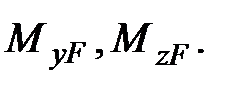
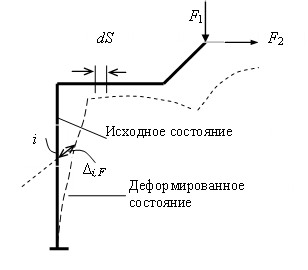
Рис.6.1. Грузовое состояние конструкции
Пусть требуется определить перемещение точки i в заданном направлении. Приложим в этом направлении единичную силу Fi=1(рис.6.2). Внутренние усилия, соответствующие этому состоянию, обозначим индексом i и чертой сверху. Таким образом, внутренние силы i-ого единичного состояния есть 
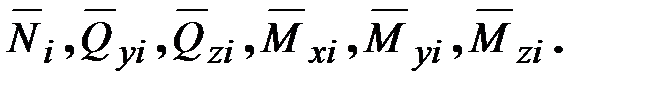
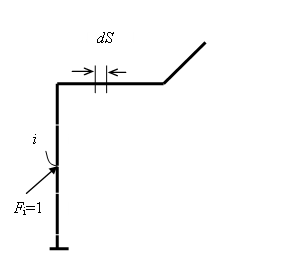
Рис. 6.2. Единичное состояние конструкции
Применим принцип возможных перемещений: если механическая система находится в равновесии, то суммарная работа внешних и внутренних сил на любых возможных бесконечно малых перемещениях, не противоречащих кинематическим связям системы, равна нулю.
При этом в качестве возможного будем рассматривать заданное состояние, а в качестве действительного — единичное состояние.
Математическая запись принципа возможных перемещений имеет вид:
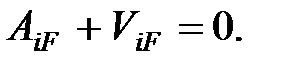 | (6.1) |
В уравнении (6.1) АiF — работа внешних сил единичного состояния на перемещениях грузового, ViF- работа внутренних сил единичного состояния на перемещениях грузового.
Работа внешних сил находится так:
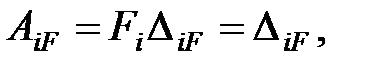 | (6.2) |
т.к. Fi=1.
Работу внутренних сил единичного состояния на перемещениях грузового найдем сначала в пределах элемента ds, причем сделаем это отдельно для каждой составляющей внутренних сил.
Растяжение-сжатие
Внутренние силы,соответствующие растяжению или сжатию,показаны на рис.6.3.
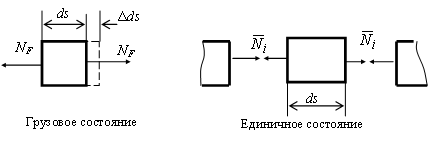
Рис.6.3. Внутренние силы, соответствующие растяжению (сжатию)
Удлинение элемента ds в грузовом состоянии равно:
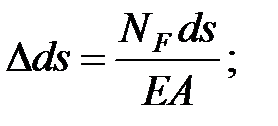
Работа внутренней продольной силы единичного состояния на этом перемещении равна:
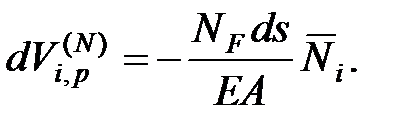 | (6.3) |
Кручение
Внутренние силы, соответствующие кручению, показаны на рис.6.4.
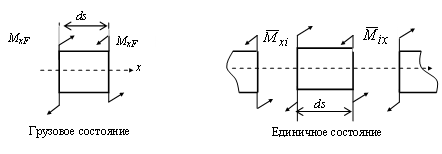
Рис.6.4. Внутренние силы, соответствующие кручению
Угол закручивания элемента ds в грузовом состоянии равен:
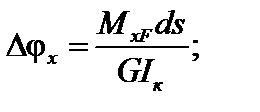
Работа внутреннего крутящего момента единичного состояния на этом перемещении равна:
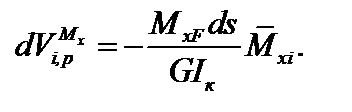 | (6.4) |
Изгиб в плоскости xoy
Найдем работу изгибающих моментов 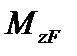 (рис.6.5).
(рис.6.5).
Взаимный угол поворота сечений элемента ds в грузовом состоянии определяется формулой (см. курс сопротивления материалов):
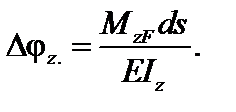
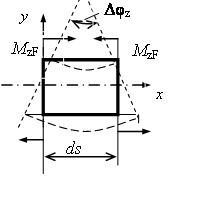
Рис.6.5.Изгиб в плоскости xoy
Работа внутренних изгибающих моментов единичного состояния на данном перемещении равна:
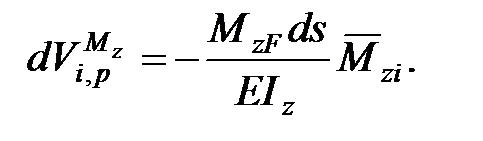 (6.5)
(6.5)
Аналогично для плоскости xoz:
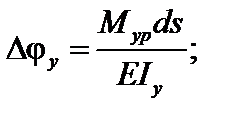
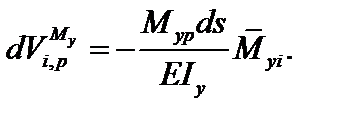 (6.6)
(6.6)
Сдвиг в плоскости xoy
Угол сдвига в плоскости xoy элемента ds, обусловленный действием поперечной силы Qy,(рис.6.6) определяется по закону Гука: 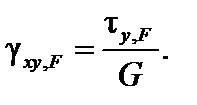 Сдвиг правой грани элемента относительно левой приводит к ее линейному смещению на величину:
Сдвиг правой грани элемента относительно левой приводит к ее линейному смещению на величину:
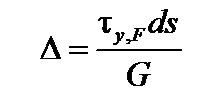 . . | (6.7) |
Рис.6.6. К определению работы поперечной силы 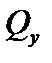
На элемент площади dA в единичном состоянии действует сила 
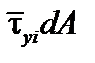 . Работа силы
. Работа силы 
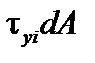 в пределах площадки dA равна:
в пределах площадки dA равна:
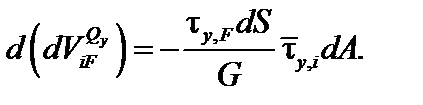 | (6.8) |
Работа сил 
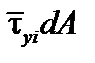 в пределах всего сечения:
в пределах всего сечения:
 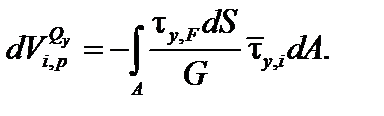 | (6.9) |
Согласно формуле Журавского 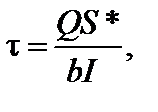 следовательно:
следовательно:
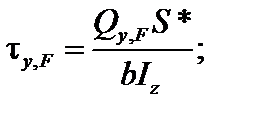 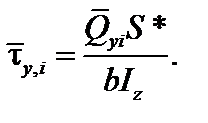 | (6.10) |
Тогда:
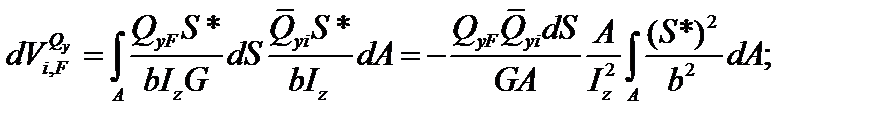 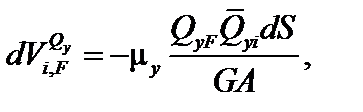 где где 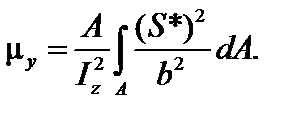 | (6.11) | ||
Аналогично для плоскости xoz имеем: 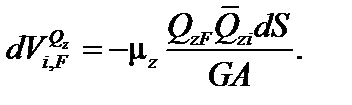 | (6.12) | ||
Работа ViF для всей конструкции:
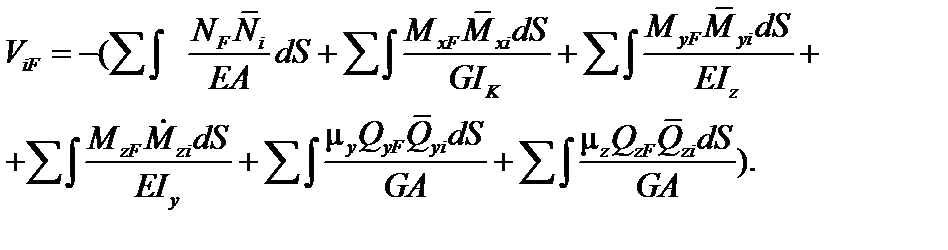 | (6.13) |
Подставляя Ai,F и ViFв формулу (6.1), находим:
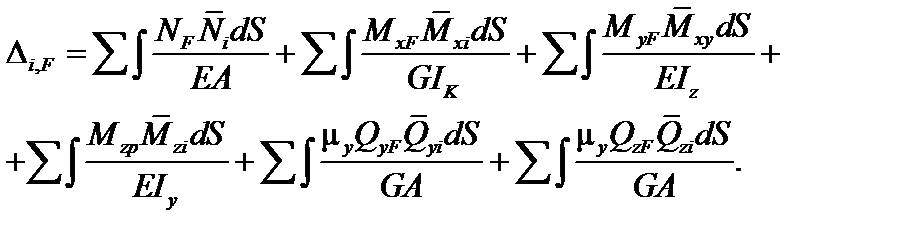 | (6.14) |
Таким образом, получена универсальная формула для вычисления перемещений от силового воздействия в стержневых системах. Эта формула называется формулой или интегралом Мора (по имени автора).
При расчете плоских стержневых систем можно пренебречь слагаемыми, определяемыми продольными и поперечными силами (ввиду их небольшого вклада). В этом случае интеграл Мора записывается в виде:
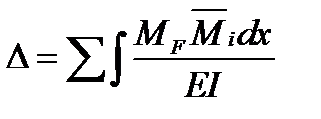 .
.
При определении перемещений в шарнирно-стержневых системах (фермах) в этой формуле остается только одно слагаемое:
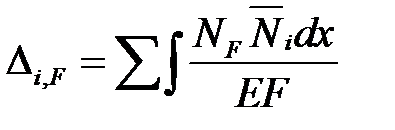 ,
,
Если продольная сила по длине стержней не меняется, то формула принимает вид:
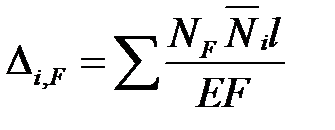 .
.
Формула Мора для конструкций, работающих на изгиб (при условии, что жесткости стержней по длине стержней не изменяются), записывается так:
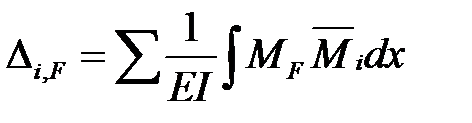
Правила вычисления интеграла Мора:
По Верещагину:
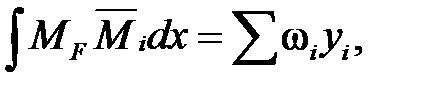
где площадь грузовой эпюры, 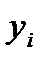 — ордината единичной эпюры, взятая под центром тяжести грузовой.
— ордината единичной эпюры, взятая под центром тяжести грузовой.
По формуле Симпсона: