Определение внутренних усилий

В дальнейшем будем рассматривать расчет трехшарнирных арок на действие только вертикальной нагрузки. Предположим, что арка нагружена, как показано на рис. 3.4,а, и для нее найдены опорные реакции. Получим формулы для определения внутренних усилий.

а б

Рис.3.4. К определению внутренних усилий в арке: а – арка в целом, б – отсеченная часть арки

Рассечем арку на две части в сечении, расположенном на расстоянии х от начала координат (рис. 3.4,б). Внутренние напряжения, действующие в сечении, заменим эквивалентным моментом М и эквивалентной силой R, а последнюю, в свою очередь, разложим на составляющие в направлении касательной N и перпендикуляра к оси арки Q. Касательную составляющую назовем продольной, а перпендикулярную составляющую —поперечной силой. Из уравнений равновесия отсеченной части легко получить следующие соотношения:

(3.5)

В формулах (3.5) есть изгибающий момент и поперечная сила в сечении x простой балки, перекрывающей тот же пролет и несущей те же нагрузки.

Для построения эпюр внутренних усилий пролет арки разбивается на несколько равных частей; по уравнению оси арки, которое обычно бывает известно, определяется угол наклона касательной φ на границах участков, и по формулам (3.5) вычисляются внутренние усилия. При наличии в каком-либо сечении внешних сосредоточенных сил и моментов внутренние силы вычисляются дважды — слева от этой силы (момента) и справа от нее.

Очертания оси арки можно выбрать таким, чтобы изгибающие моменты во всех сечениях были равны нулю. Из первой формулы (3.5) имеем:

Отсюда:

Таким образом, если принять ординаты оси арки равными балочному изгибающему моменту, деленному на величину распора, изгибающие моменты в такой арке будут равны нулю. Такие ординаты оси арки являются наиболее рациональными при данной нагрузке.

ПРИМЕРЫ РАСЧЕТА ТРЕХШАРНИРНОЙ АРКИ

Пример 1.

Для сплошной трехшарнирной арки (рис.3.5) требуется определить аналитически изгибающие моменты, поперечные и продольные силы в сечениях к₁ и к₂ от действия постоянной заданной нагрузки.

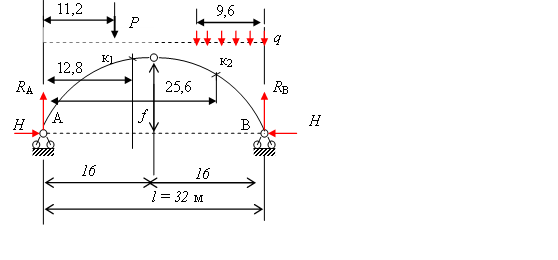
Рис.3.5.К примеру 1

Дано: ℓ = 32м;q = 6кН/м;f/ℓ = 0,35; Р = 3кН.

Очертание оси арки — окружность:

,

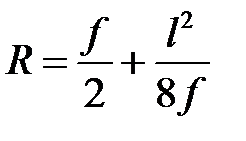где R— радиус окружности, по которой очерчена арка.

Уравнение оси:

;

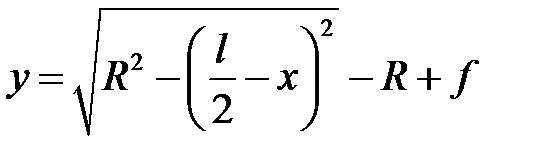Функции угла наклона касательной: .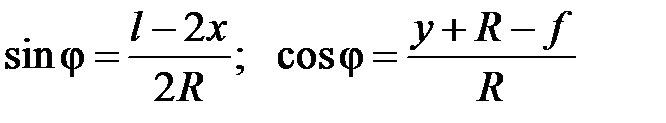

Решение:

1) Вычисление геометрических характеристик:

f = 0,35ℓ = 0,35 × 32 = 11,2 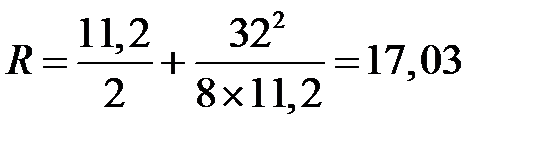м;

м;

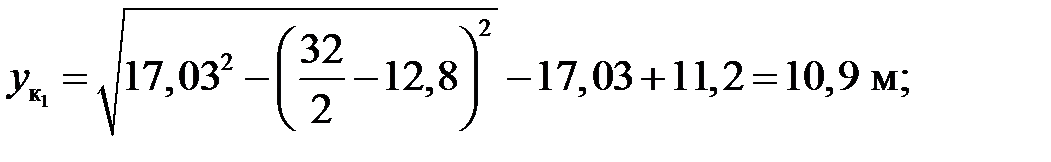
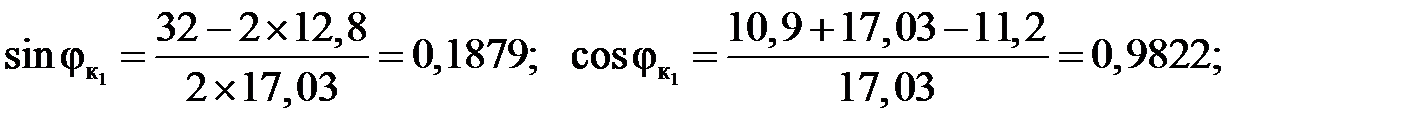
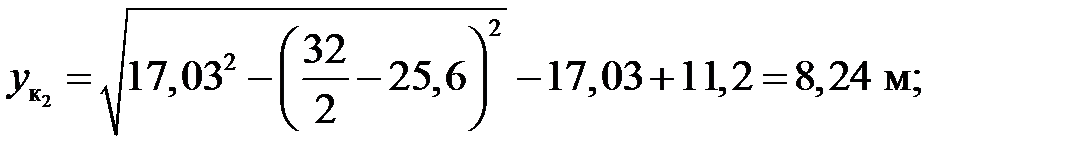
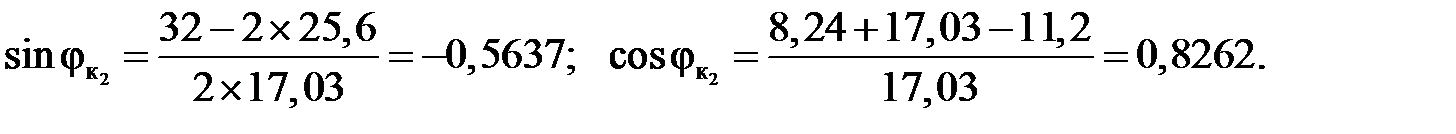
2) Вычисление опорных реакций:

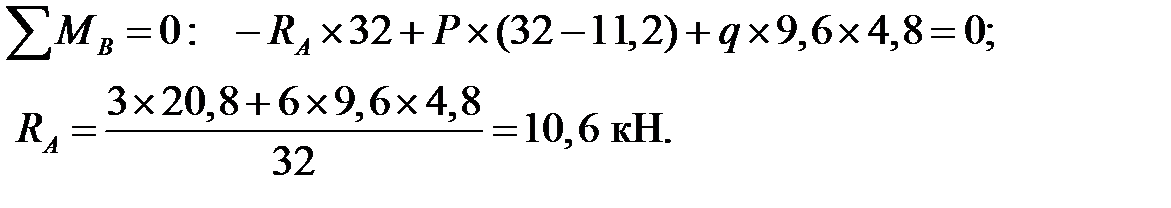
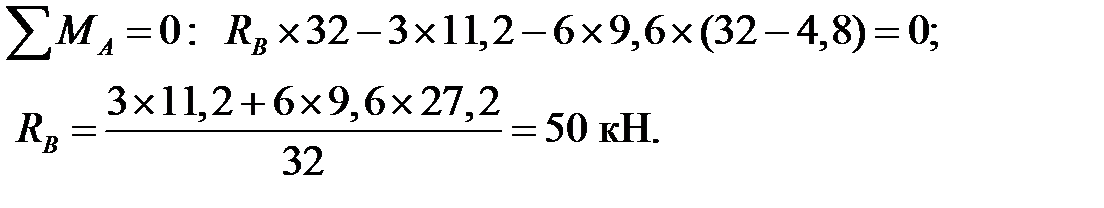
Проверка:

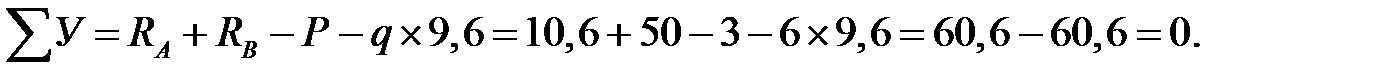Вертикальные реакции найдены верно.

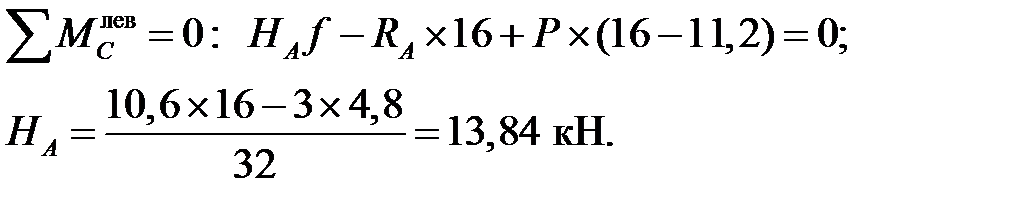
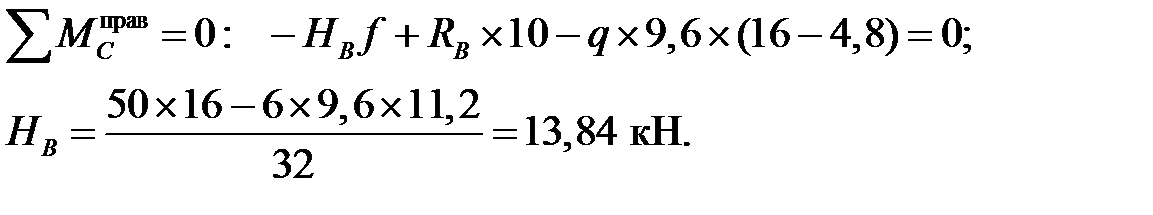
Поверка:

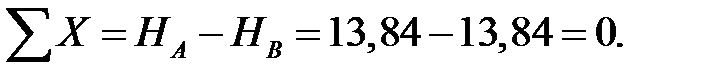
Горизонтальные реакции найдены верно.

3) Вычисление внутренних усилий:

балочные значения:

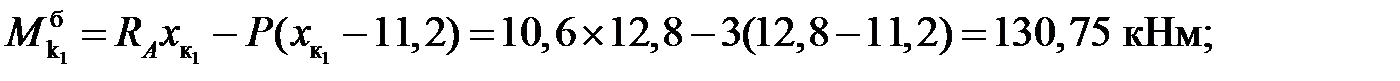
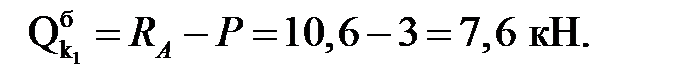
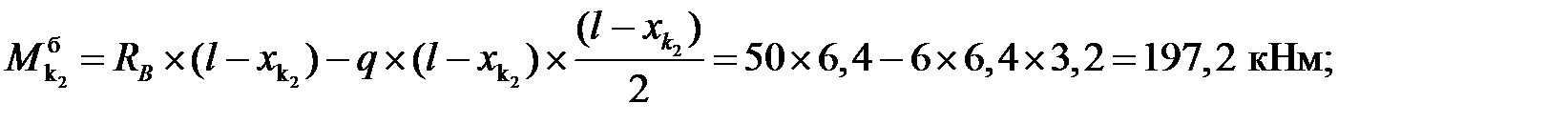
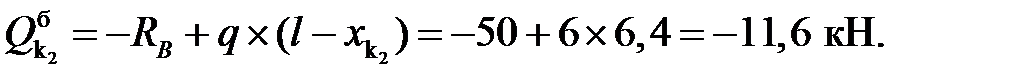
Усилия в сечениях арки:

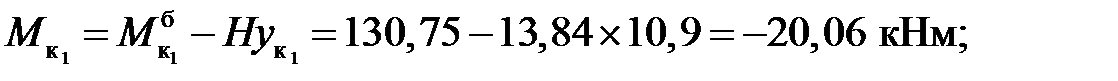
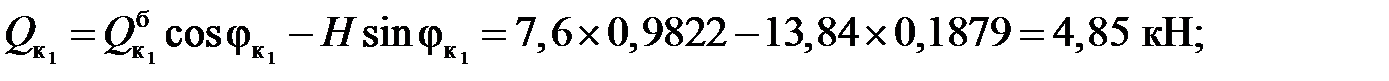
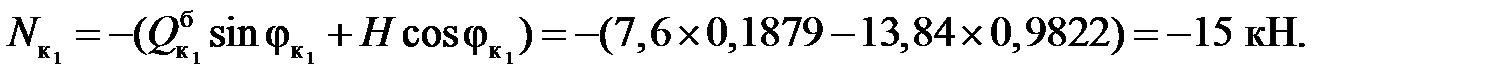
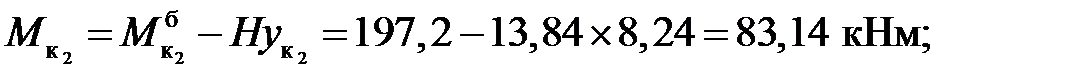
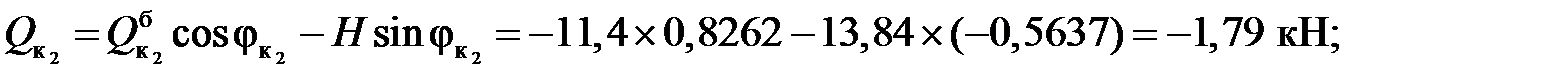
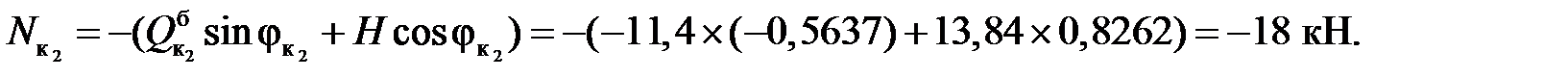
Пример2. Определить изгибающие моменты, поперечные и продольные силы в сечениях к₁ и к₂ арки (рис.3.6) от действия заданной нагрузки.

Дано: Р= 6 кН,q=4 кН/м, l=20 м, f=6 м, ось арки — парабола.

Уравнение оси:

.

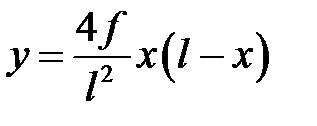Решение.

1. Вычисление геометрических характеристик сечений.

По уравнению оси находим:

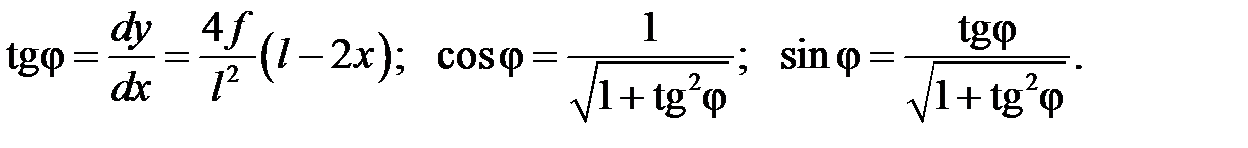
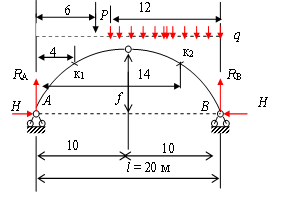
Рис.3.6. К примеру 2

Ординаты сечений:

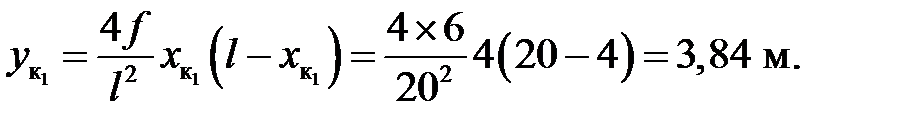
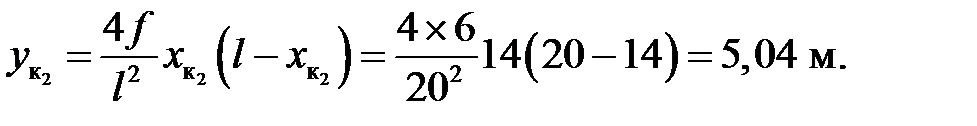
Характеристики углов наклона касательных к оси:

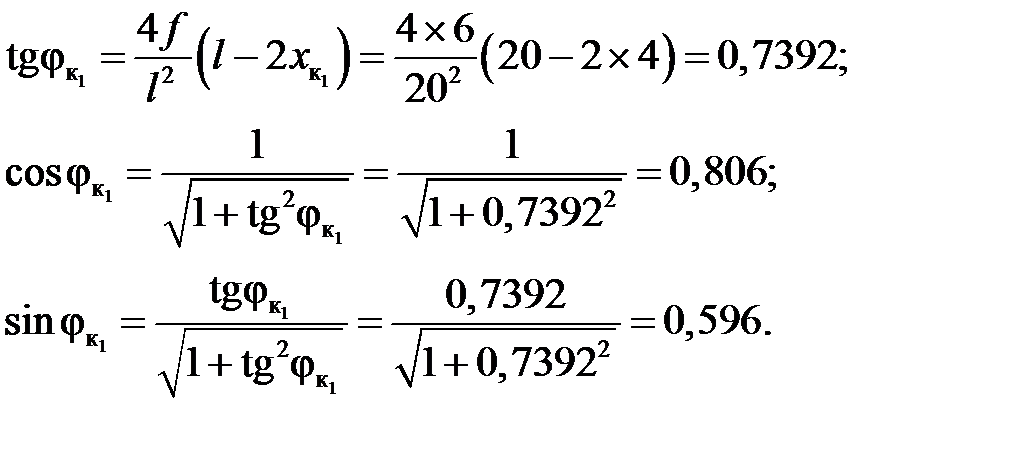
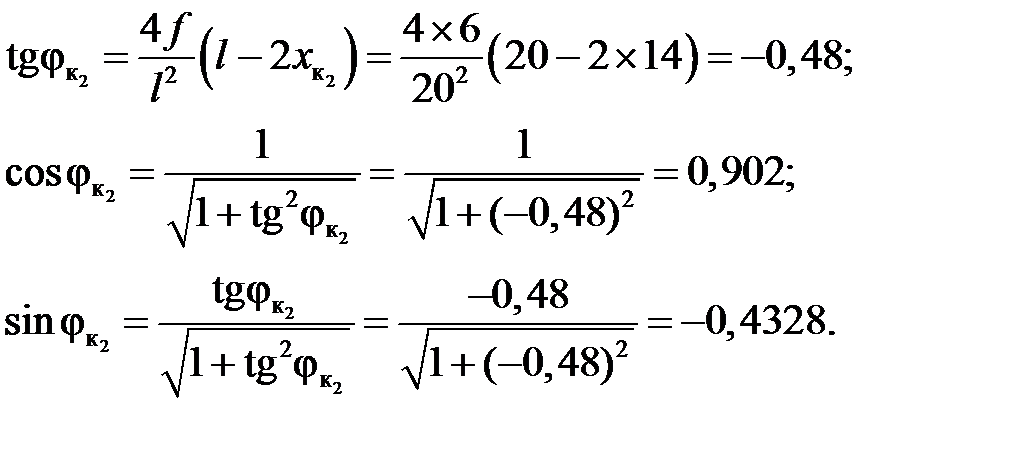
2. Определение опорных реакций:

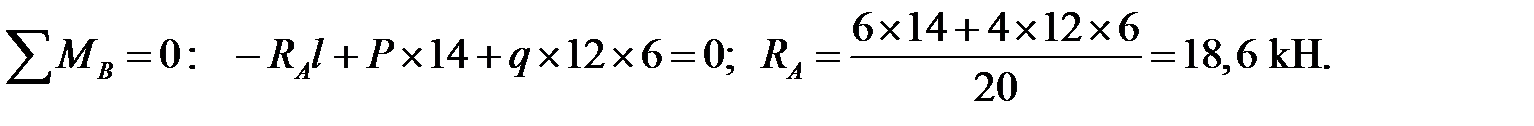
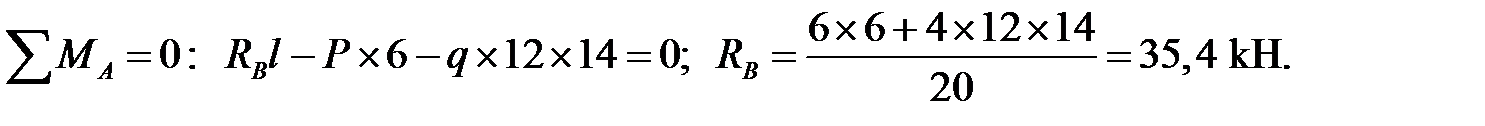
Проверка:

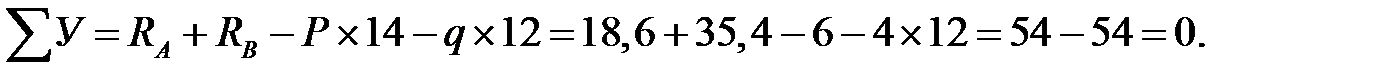
Вертикальные реакции найдены верно.

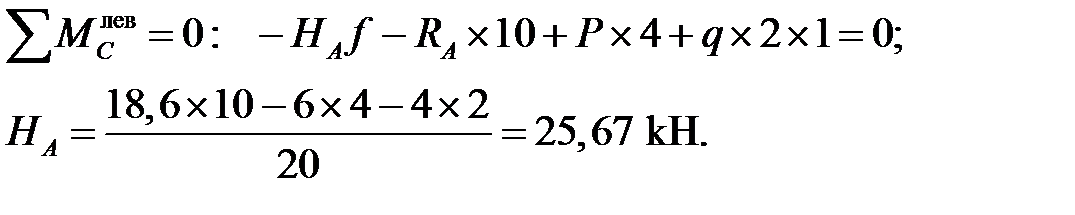
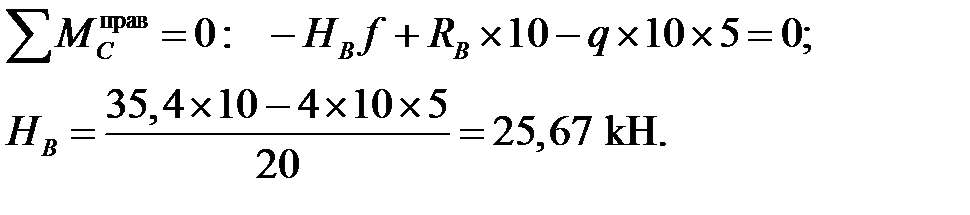
Поверка:

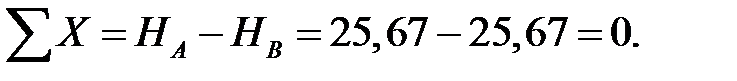
Горизонтальные реакции найдены верно.

3. Вычисление внутренних усилий:

балочные значения:

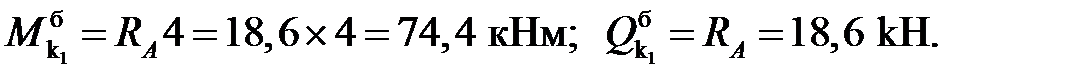
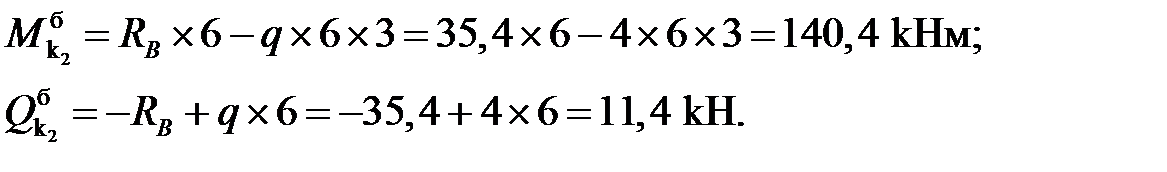
Усилия в сечениях арки:

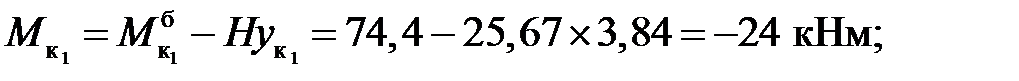
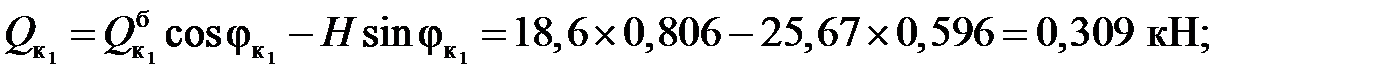
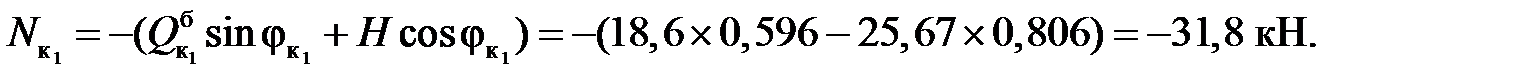
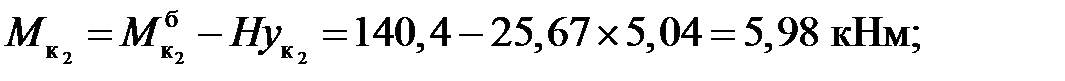
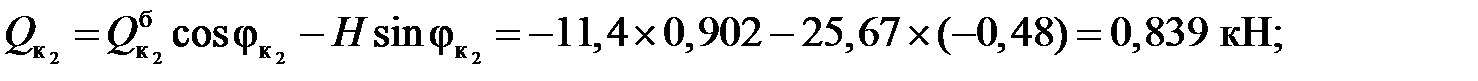
ЛЕКЦИЯ 4. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ФЕРМЫ