Статически определимых балках

Простые двухопорные или консольные балки (рис.2.4) находят широкое применение в различных объектах техники. Однако при увеличении длины пролета применение таких балок становится экономически невыгодным, так как при этом существенно увеличиваются изгибающие моменты, и приходится использовать балки большого поперечного сечения. Снизить значения изгибающих моментов можно за счет использования для перекрытия того же пролета нескольких простых балок, как показано, например, на рис.2.5. Взяв две балки длиной l/2 каждая (рис.2.5), можно уменьшить максимальные значения моментов в четыре раза. Однако еще большего эффекта можно добиться, используя многопролетные статически определимые балки специальной конструкции. Такие балки образуются одним из двух способов.

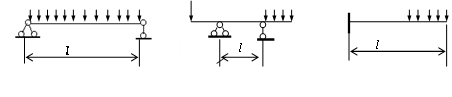
Рис.2.4. Простые балки

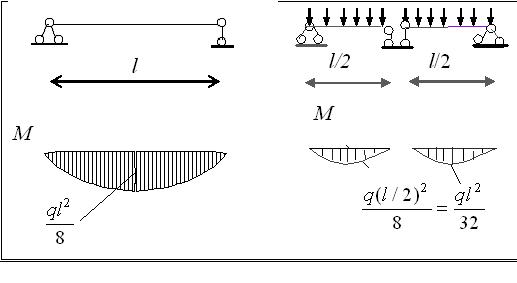
Рис.2.5. Перекрытие пролета двумя балками

Первый способ. К простой двухопорной или консольной балке присоединяется новая балка с помощью шарнира и одного опорного стержня. К полученной неизменяемой и статически определимой системе аналогичным способом крепится другая балка и т.д. (рис. 2.6).

Таким способом можно получить статически определимую балку с любым количеством пролетов.

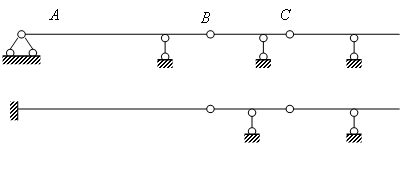
Рис.2.6. Образование многопролетной балки по первому способу

Второй способ. Между двумя простыми балками, одна из которых может быть двухопорной или защемленной одним концом, а вторая должна быть двухопорной (с двумя вертикальными опорными стержнями), вставляется третья балка, которая крепится к первым двум с помощью шарниров (рис. 2.7). В результате образуется геометрически неизменяемая и статически определимая система. Процесс образования можно представить как присоединение к неизменяемой системе АВ диска СD с помощью трех стержней 1,2 и 3, не пересекающихся в одной точке и не параллельных друг другу. Описанные выше способы можно комбинировать.

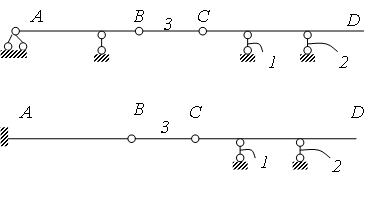
Рис. 2.7. Образование многопролетной балки по второму способу

Пример многопролетной статически определимой балки, образованной комбинированным способом, показан на рис. 2.8.

Рис. 2.8.Образование многопролетной балки комбинированным способом

Для того, чтобы рассчитать любую из изображенных на рис. 2.6-2.8 многопролетных балок на действие заданных нагрузок, необходимо прежде всего найти усилия во всех внешних и внутренних связях, использованных для образования системы. Для этого нужно мысленно расчленить систему на отдельные балки в местах их соединения шарнирами, приложить к балкам силы взаимодействия и составить для каждой из них уравнения равновесия. Проиллюстрируем сказанное на примере расчета балки (см. рис. 2.6). Пусть балка нагружена, как показано на рис. 2.9.

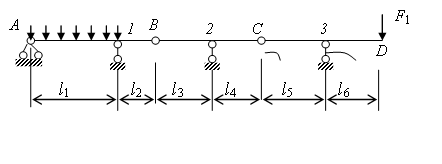
Рис.2.9. К расчету многопролетной балки

Расчленим заданную конструкцию на три части в местах их соединения шарнирами, т.е. в точках В и С, и покажем силы взаимодействия в этих точках. Расчлененная конструкция показана на рис. 2.10.

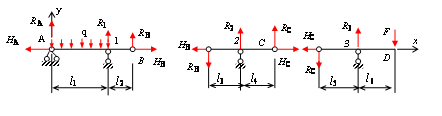
Рис.2.10. Схема взаимодействия балок в конструкции

Составим теперь уравнения равновесия для балок АВ, ВС и СD.

Балка АВ:

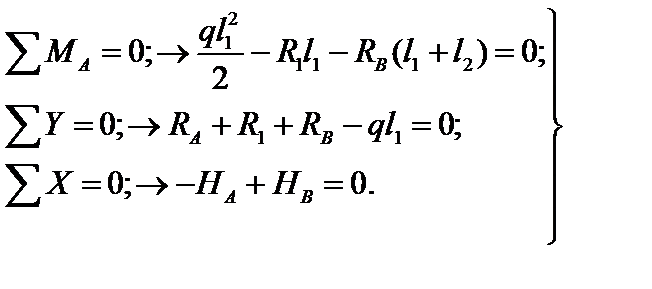(2.1)

Балка ВС:

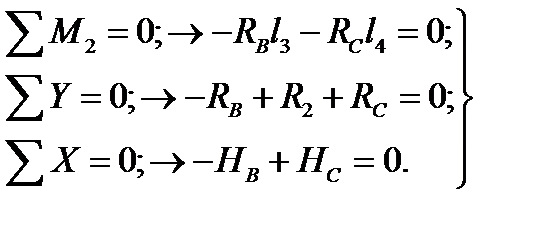(2.2)

Балка СD:

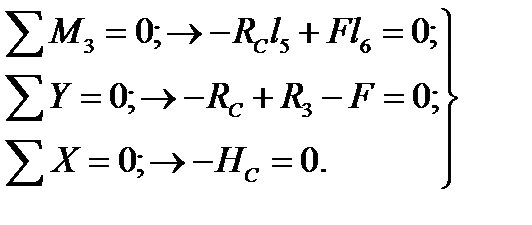(2.3)

Получили систему из 9 уравнений с 9 неизвестными: 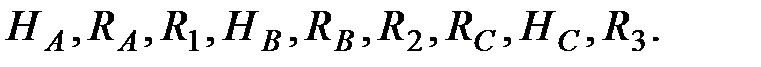Решив эту систему, найдем перечисленные выше реакции. Дальнейший расчет каждой балки в отдельности может быть выполнен методами сопротивления материалов. Анализ уравнений (2.1)-(2.2) показывает, что система трех уравнений равновесия балки АВ (2.1) содержит 5 неизвестных: 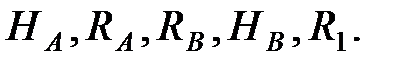Система трех уравнений равновесия балки ВС также содержит 5 неизвестных: 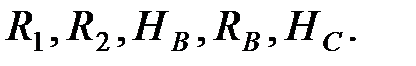И, наконец, система трех уравнений равновесия балки СD (2.3) содержит 3 неизвестных: Таким образом, нет необходимости решать уравнения (2.1)-(2.3) как систему связанных уравнений. Можно решить отдельно уравнения (2.3) и из них найти Затем из уравнений (2.2) при известных 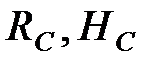можно найти 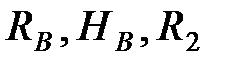, после чего из уравнений (2.1) можно определить 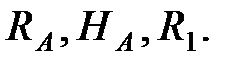Следовательно, правильный выбор последовательности расчета существенно упрощает вычисления. Сделать такой выбор позволяет анализ взаимодействия отдельных балок. В конструкции, изображенной на рис. 2.9 основной является балка АВ, она имеет шарнирно-неподвижную и шарнирно-подвижную опоры и вследствие этого является геометрически неизменяемой и статически определимой. На нее в точке В опирается балка ВС, имеющая дополнительную шарнирно-подвижную опору в точке 2. В свою очередь, точку С можно рассматривать как шарнирно-неподвижную опору для балки СD. Наряду с шарнирно-подвижной опорой в точке 3, эта опора обеспечивает неизменяемость балки СD. Описанная схема взаимодействия изображена на рис. 2.11.

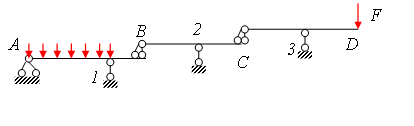
Рис.2.11. Поэтажная схема балки

Подобные схемы иногда называют поэтажными. Нетрудно убедиться, что если начать расчет с самой верхней на поэтажной схеме балки, то это приведет к трем системам уравнений, которые были описаны выше на основе анализа уравнений (2.1)-(2.3).

Схема взаимодействия или поэтажная схема для многопролетной балки рис. 2.8. приведена на рис. 2.12.

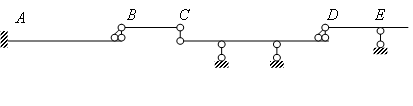
Рис.2.12. Поэтажная схема

ПРИМЕР РАСЧЕТА МНОГОПРОЛЕТНОЙ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ БАЛКИ

Пример1: Построить эпюры изгибающих моментов и поперечных сил для балки, изображенной на рис.2.13, а.

Решение:

Конструкция состоит из двух балок 1-3 и 3-6. Балка 1-3 является основной, так как она может самостоятельно нести приложенные к ней нагрузки. Балка 3-6 является подвесной. В точке 3 она опирается на основную балку и имеет одну опору в точке 5. Схема взаимодействия балок (поэтажная схема) приведена на рис.2.13,б.

Расчет начинаем с верхней на поэтажной схеме балки 3-6. Эпюры изгибающих моментов и поперечных сил для этой балки, полученные методами сопротивления материалов, приведены на рис.2.13,в. При этом предварительно были найдены реакции балки 3-6 на опоре 3. На втором этапе рассчитываем балку 1-3, приложив к ней наряду с заданными внешними силами давление, которое передается с вышележащей балки3-6. Это давление равно взятой с обратным знаком реакции балки 3-6 на опоре 3. Результаты расчета балки 1-3 приведены на рис. 2.13,г. Чтобы получить окончательные результаты для заданной многопролетной балки, необходимо объединить эпюры, полученные для составляющих простых балок.

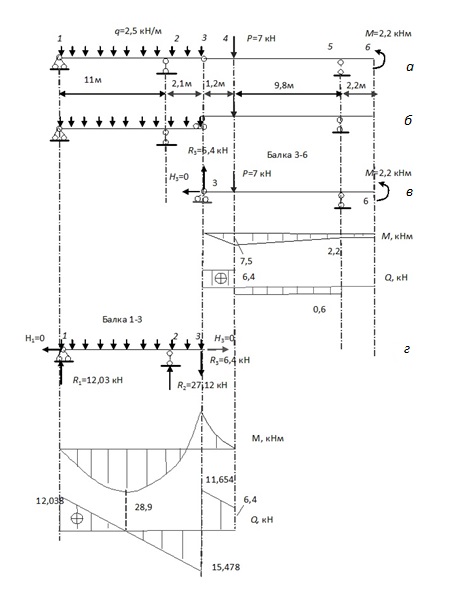
Рис.2.1. К расчету составной балки: а – заданная балка, б – поэтажная схема, в – подвесная балка, г – главная балка