Тема 6 Определенный интеграл
Задача 1.Вычислить,площадь фигуры, ограниченной линиями у=х2+4x, у=х+4 (рис. 1).
Решение. Площадь S фигуры, ограниченной сверху н снизу непрерывными линиями у=f(х) и у= 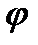 (х), пересекающимися вточках с абсциссами x=а и х=b, определяется по формуле
(х), пересекающимися вточках с абсциссами x=а и х=b, определяется по формуле
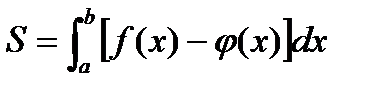 (1)
(1)
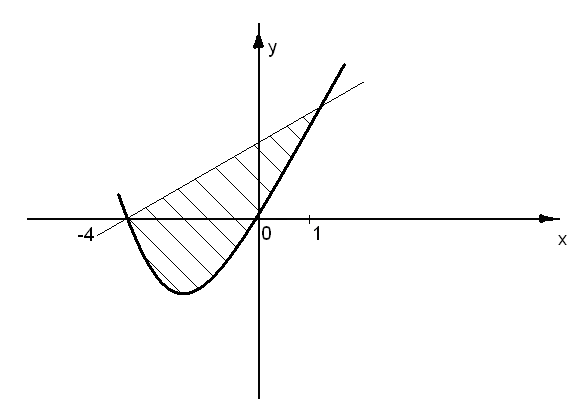
Рис. 1
Для нахождения точек пересечения данных линий решаем систему уравнений
y= х2+4х,
у = х+4.
х2+4х=х+4, х2+3х-4=0, откуда x1=- 4, х2=1.
Применяя формулу (1), получим:
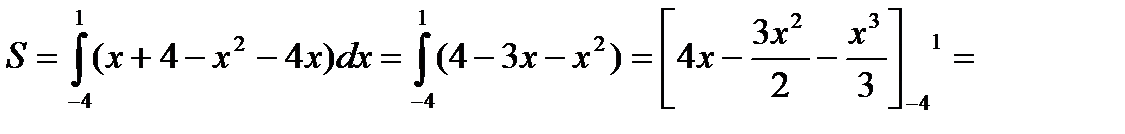
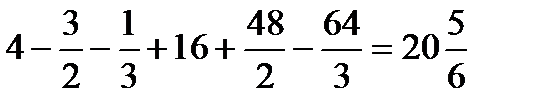 (кв.ед.)
(кв.ед.)
Вопросы для самопроверки
1. Назовите задачи, приводящие к понятию определенного интеграла.
2. Напишите интегральную сумму для функции у=f(х) на отрезке [а; b]
3. Что называется определенным интегралом от функциями y=f(х) на отрезке [а; b]?
4. Каков геометрический смысл определенного интеграла?
5. Перечислите основные свойства определенного интеграла.
6. Чему равна производная от определенного интеграла с переменным верхним пределом интегрирования?
7. Напишите формулу Ньютона — Лейбница.
8. Напишите формулу интегрирования по частям в определенном интеграле.
9. Как вычислить объем тела, образованного вращением плоской фигуры вокруг оси Ох? оси Оу?
10. Дайте определение несобственного интеграла с бесконечными пределами интегрирования.
11. Сформулируйте понятие несобственного интеграла от разрывной функции.
Задания для контрольной работы
Задание 1
В задачах 1 – 20 найти указанные пределы.
1. а) 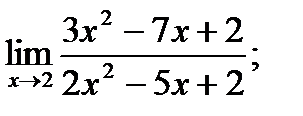 б)
б) 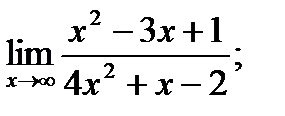
в) 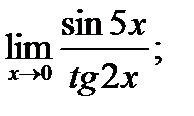 г)
г) 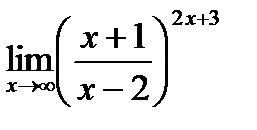 .
.
2. а) 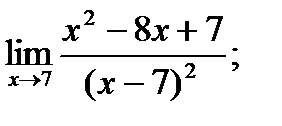 б)
б) 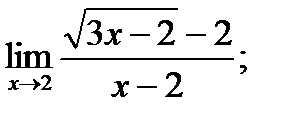
в) 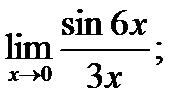 г)
г) 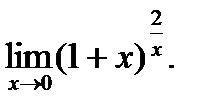
3. а) 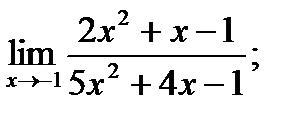 б)
б) 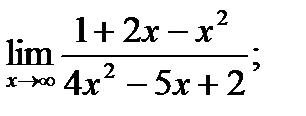
в) 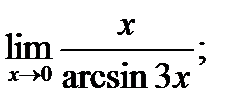 г)
г) 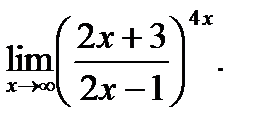
4. а) 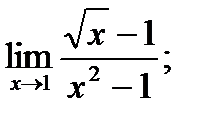 б)
б) 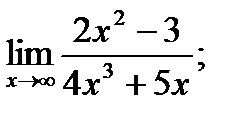
в) 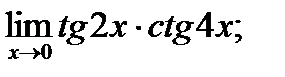 г)
г) 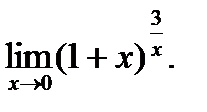
5. а) 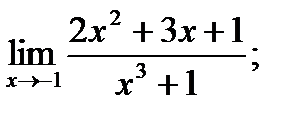 б)
б) 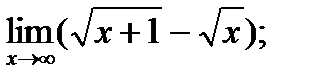
в) 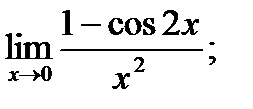 г)
г) 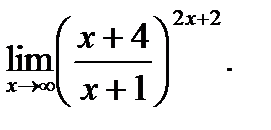
6. а) 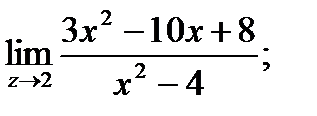 б)
б) 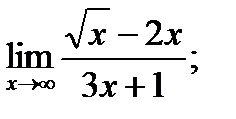
в) 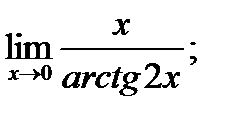 г)
г) 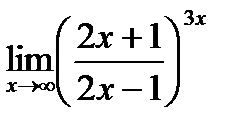 .
.
7. а) 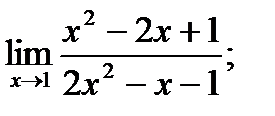 б)
б) 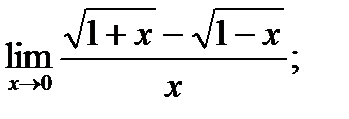
в) 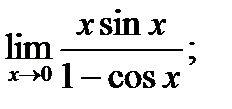 г)
г) 
8. а) 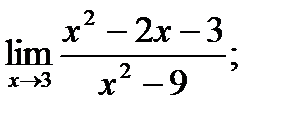 б)
б) 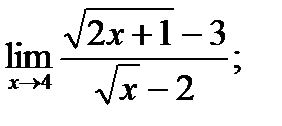
в) 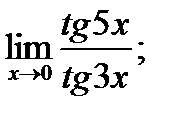 г)
г) 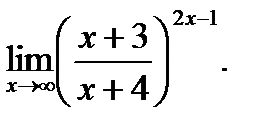
9. a) 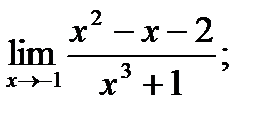 б)
б) 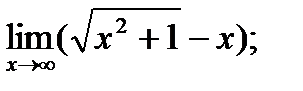
в) 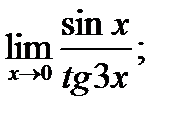 г)
г) 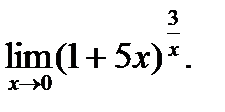
10. а) 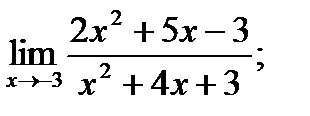 б)
б) 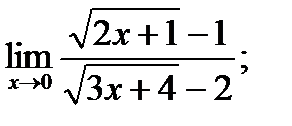
в) 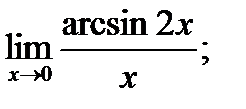 г)
г) 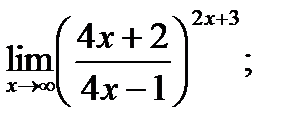
11. а) 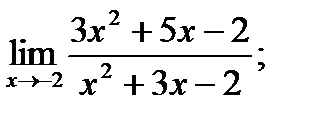 б)
б) 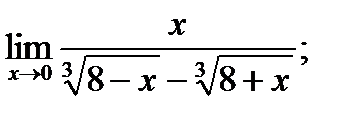
в) 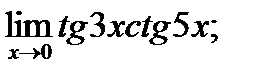 г)
г) 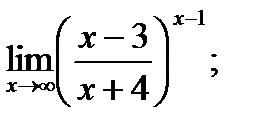
12. а) 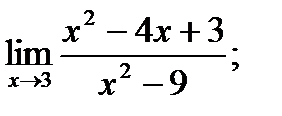 б)
б) 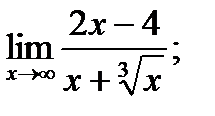
в) 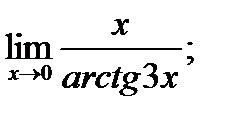 г)
г) 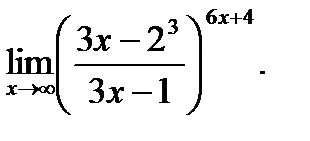
13. а) 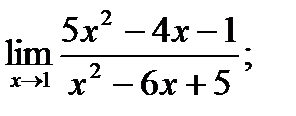 б)
б) 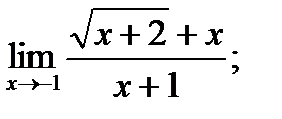
в) 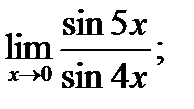 г)
г) 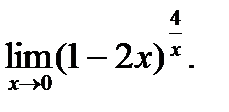
14. а) 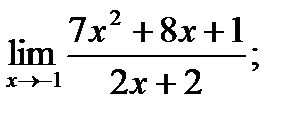 б)
б) 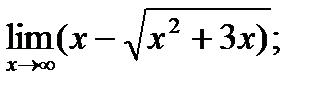
в) 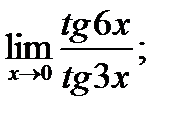 г)
г) 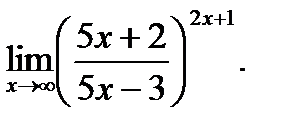
15. а) 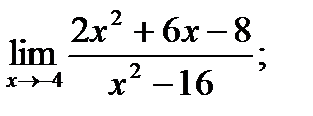 б)
б) 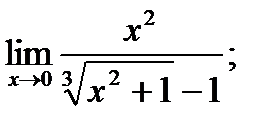
в) 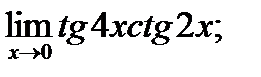 г)
г) 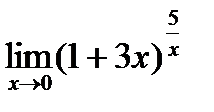
16. а) 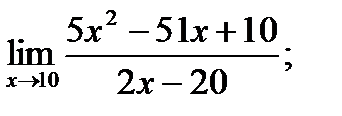 б)
б) 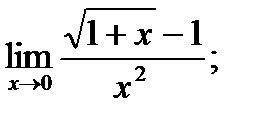
в) 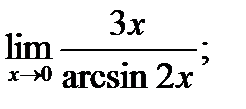 г)
г) 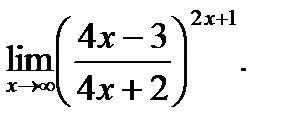
17. а) 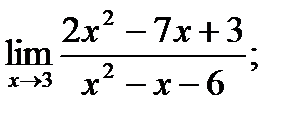 б)
б) 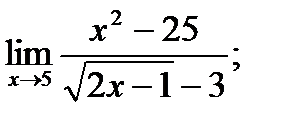
в) 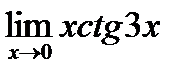 ; г)
; г) 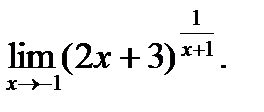
18. а) 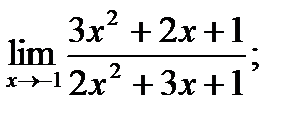 б)
б) 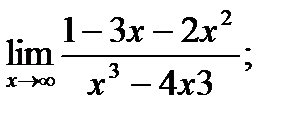
в) 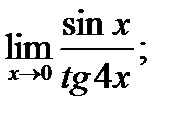 г)
г) 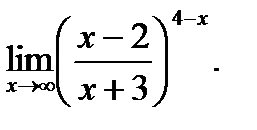
19. а) 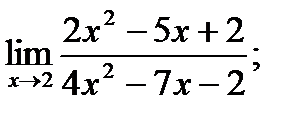 б)
б) 
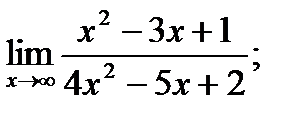
в) 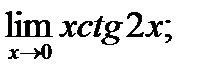 г)
г) 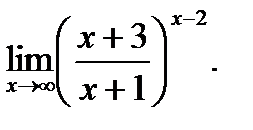
20. а) 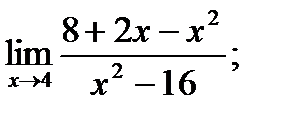 б)
б) 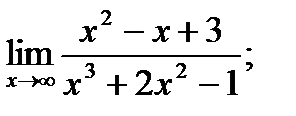
в) 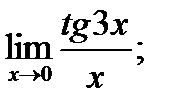 г)
г) 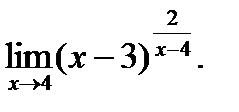
Задание 2
В задачах 1 – 20 найти производные заданных функций:
1. а) 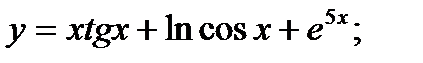 б)
б) 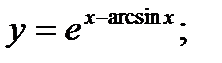 в)
в) 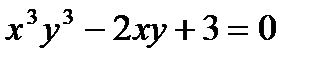 .
.
2. а) 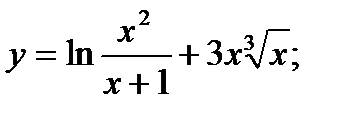 б)
б) 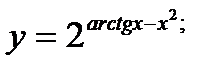 в)
в) 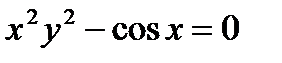 .
.
3. а) 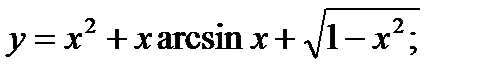 б)
б) 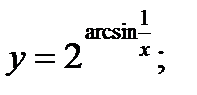 в)
в) 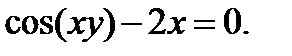
4. а) 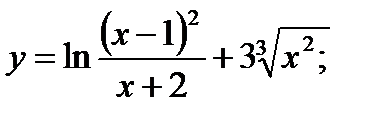 б)
б) 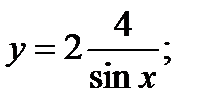 в)
в) 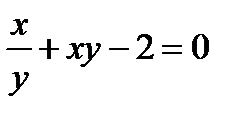 .
.
5. а) 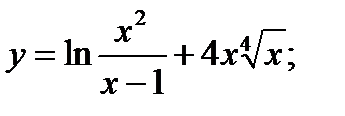 б)
б) 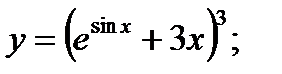 в)
в) 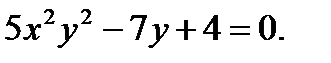
6. а) 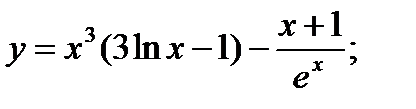 б)
б) 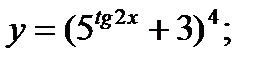 в)
в) 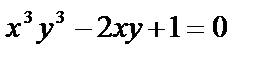 .
.
7. а) 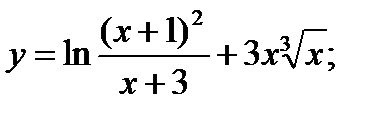 б)
б) 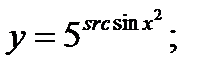 в)
в) 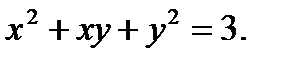
8. а) 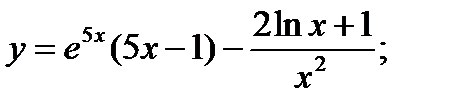 б)
б) 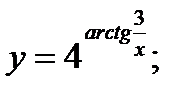 в)
в) 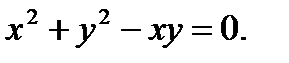
9. а) 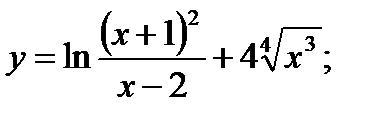 б)
б) 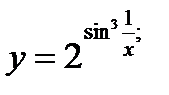 в)
в) 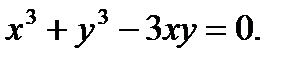
10. а) 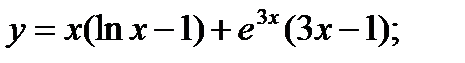 б)
б) 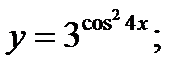 в)
в) 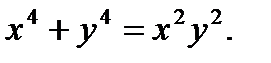
11. а) 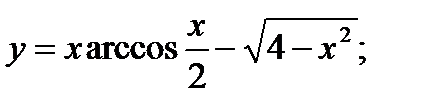 б)
б) 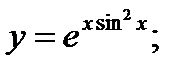 в)
в) 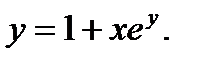
12. а) 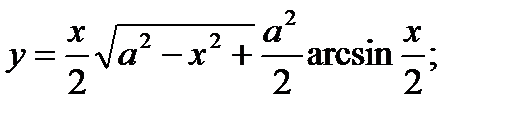 б)
б) 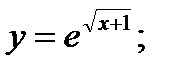 в)
в) 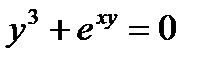 .
.
13. а) 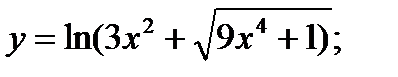 б)
б) 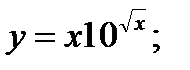 в)
в) 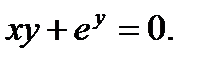
14. а) 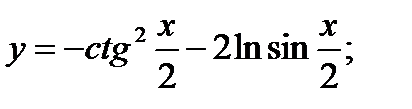 б)
б) 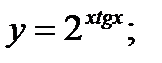 в)
в) 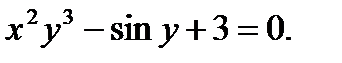
15. а) 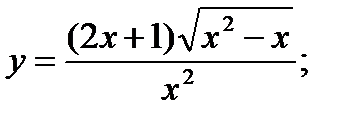 б)
б) 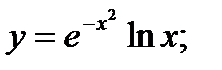 в)
в) 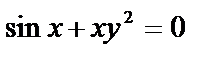
16. а) 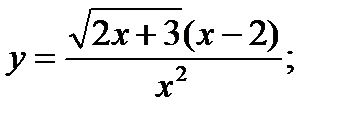 б)
б) 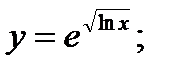 в)
в) 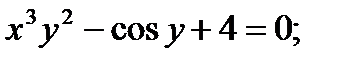
17. а) 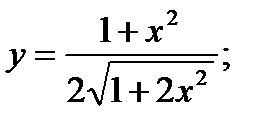 б)
б) 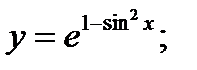 в)
в) 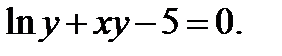
18. а) 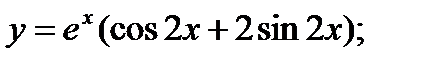 б)
б) 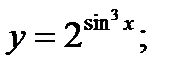 в)
в) 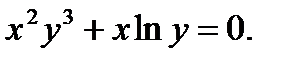
19. а) 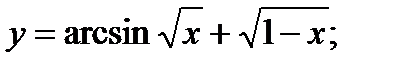 б)
б) 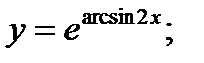 в)
в) 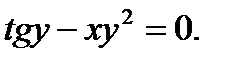
20. а) 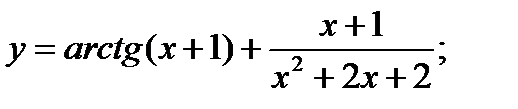 б)
б) 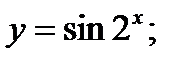 в)
в) 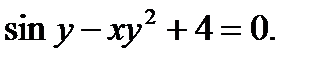
Задание 3
В задачах 1-20 исследовать функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проверить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и ее точки экстремума; 5) найдите интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.
1. 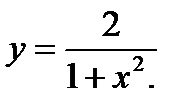 2.
2. 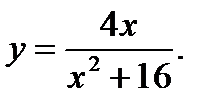 3.
3. 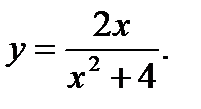
4. 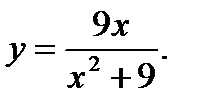 5.
5. 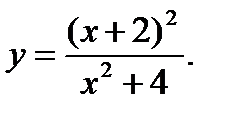 6.
6. 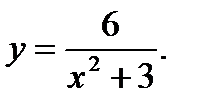
7. 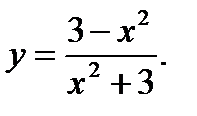 8.
8. 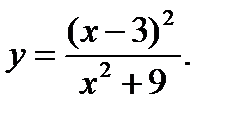 9.
9. 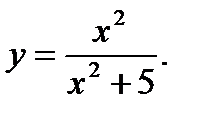
10. 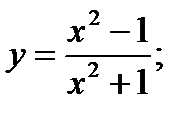 11.
11. 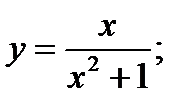 12.
12. 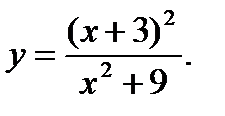
13. 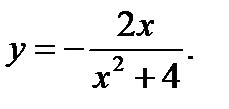 14.
14. 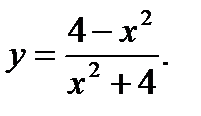 15.
15. 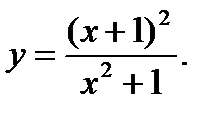
16. 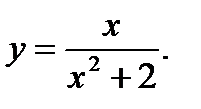 17.
17. 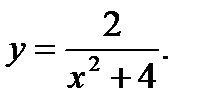 18.
18. 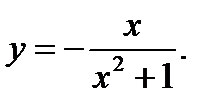
19. 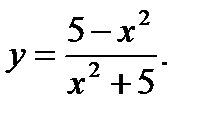 20.
20. 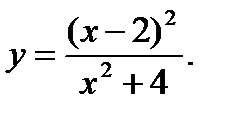
Задание 4
Данную функцию z=f(x, y) исследовать на экстремум.
1. z= 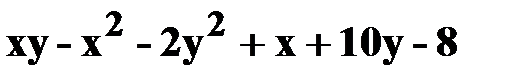 .
.
2. z= 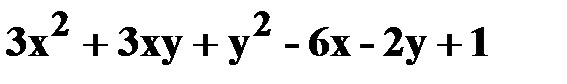 .
.
3. z= 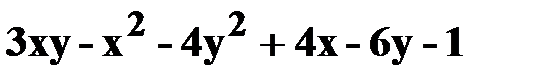 .
.
4. z= 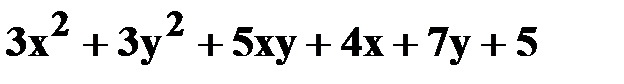
5. z= 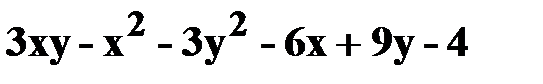 .
.
6. z= 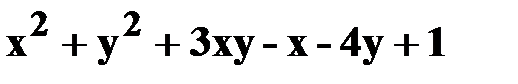 .
.
7. z= 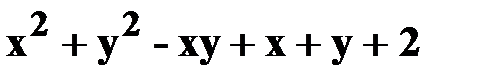 .
.
8. z= 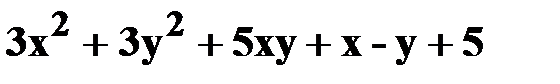 .
.
9. z= 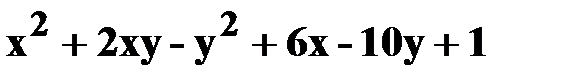 .
.
10. z= 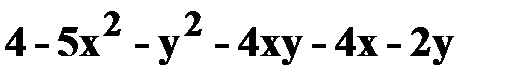 .
.
11. z= 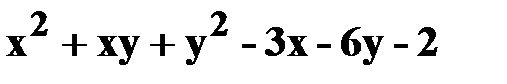 .
.
12. z= 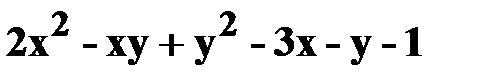 .
.
13. z= 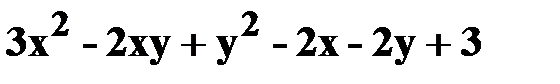 .
.
14. z= 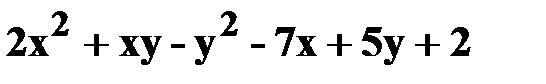 .
.
15. z= 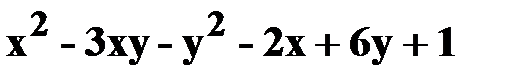 .
.
16. z= 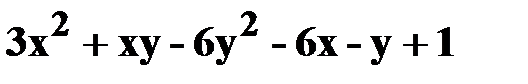 .
.
17. z= 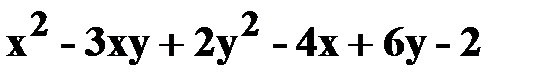 .
.
18. z= 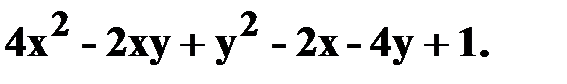
19. z=  .
.
20. z= 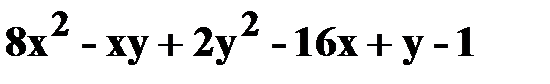 .
.
Задание 5
В задачах 1 – 20 найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.
1. а) 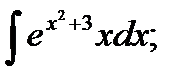 б)
б) 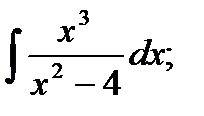 в)
в) 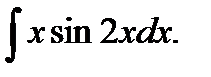
2. а) 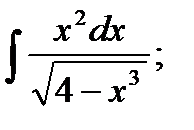 б)
б) 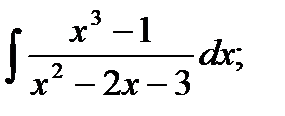 в)
в) 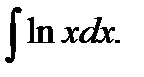
3. а) 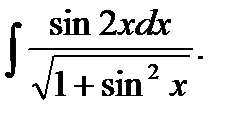 б)
б) 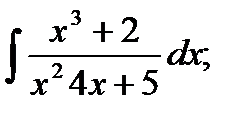 в)
в) 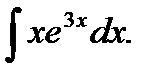
4. а) 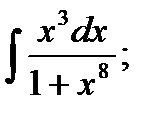 б)
б) 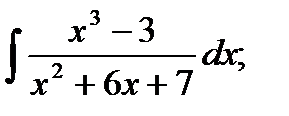 в)
в) 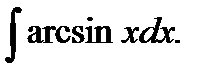
5. а) 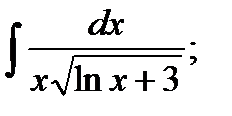 б)
б) 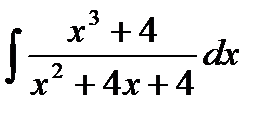 ; в)
; в) 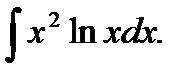
6. а) 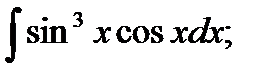 б)
б) 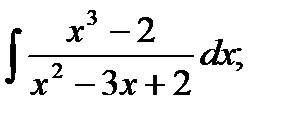 в)
в) 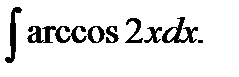 .
.
7. а) 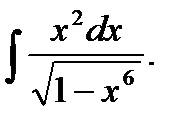 б)
б) 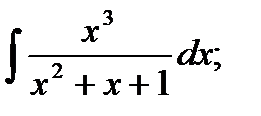 в)
в) 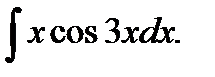
8. а) 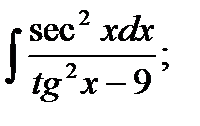 б)
б) 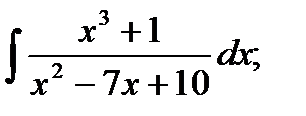 в)
в) 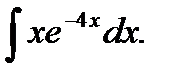
9. а) 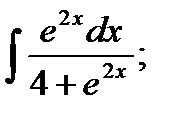 б)
б) 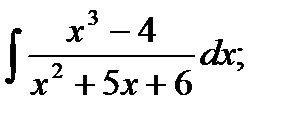 в)
в) 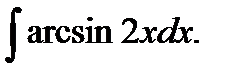
10. а) 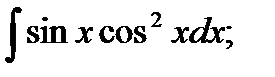 б)
б) 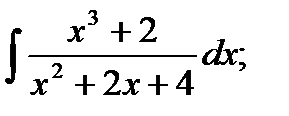 в)
в) 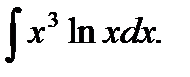
11. а) 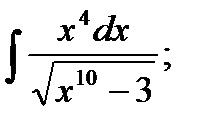 б)
б) 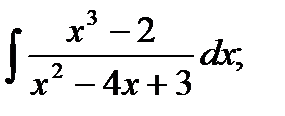 в)
в) 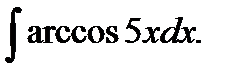
12.а) 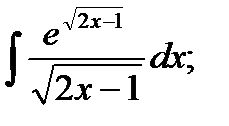 б)
б) 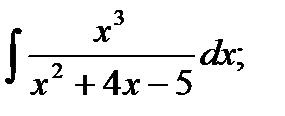 в)
в) 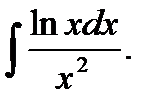
13. а) 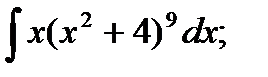 б)
б) 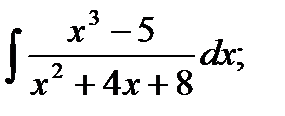 в)
в) 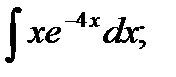
14. а) 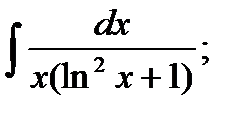 б)
б) 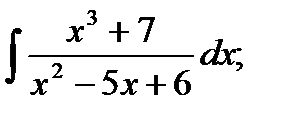 в)
в) 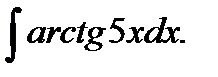
15. а) 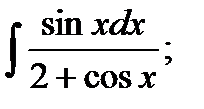 б)
б) 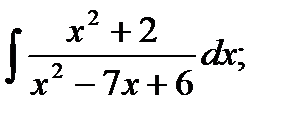 в)
в) 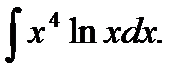
16. а) 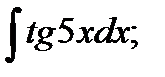 б)
б) 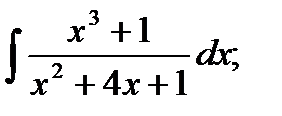 в)
в) 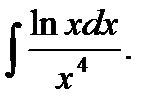
17. а) 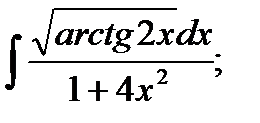 б)
б) 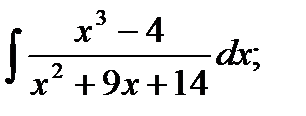 в)
в) 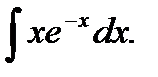
18. а) 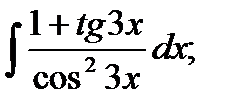 б)
б) 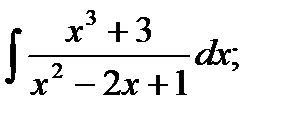 в)
в) 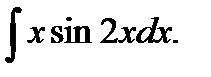
19. а) 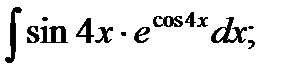 б)
б) 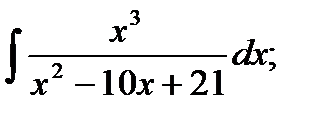 в)
в) 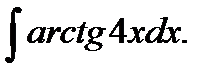
20. а) 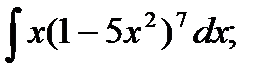 б)
б) 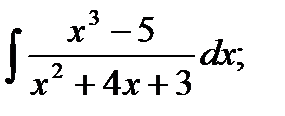 в)
в) 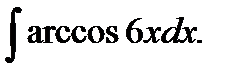
Задание 6
В задачах 1 – 10 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
1. у = х3; у = 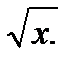 2. у =
2. у = 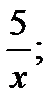 у = 6 – х .
у = 6 – х .
3. у = 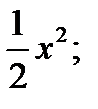 у = 4 – х . 4. у = х2+2; у = 4 – х2.
у = 4 – х . 4. у = х2+2; у = 4 – х2.
5. у = - х2+1; у = х – 1. 6. у = x2 – 4x+4; y=x.
7. y = 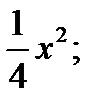 y = 4x. 8. y =
y = 4x. 8. y = 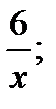 y = 7 – x.
y = 7 – x.
9. y = 3x2+1; y = 3x+7. 10. y = 2x – x2; y = - x.
В задачах 11 – 15 вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями. Сделать чертеж.
11. y2 = x; y = x2. 12. xy = 4; x = 1; x = 4; y = 0.
13.y = sin x (одна полуволна); y = 0. 14. y = x2+1; y = 3x – 1.
15. 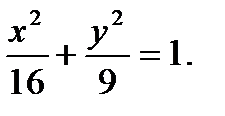
В задачах 16 – 20 вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной указанными линиями. Сделать чертеж.
16. y2 =4 – x ; x=0. 17. 
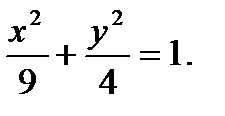
18. x + y – 2 =0; x=0; y=0. 19. xy =2; x=0; y=1; y=4.
20. y =-x2+4; x=0; y=0; y=3.
Литература
1 Письменный Д.Т. Конспект лекций по высшей математике (ч. 1,2)./Письменный Д.Т.-М.:«Айрис-пресс»,2007.-282с., 253с.
2 Лунгу К.Н. Сборник задач по высшей математике.(ч.1,2) -М.: «Айрис - пресс», 2008-574с.
Дополнительная литература
1 Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие / Н.С. Пискунов. –М.: Интеграл-Пресс. -2007.Ч.1. -415с.
2 Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие / Н.С. Пискунов. –М.: Интеграл-Пресс. -2006. Ч.2.-544с.
3 Данко П.Е., Попов А.Г. Высшая математики в упражнениях и задачах. / Данко П.Е. Попов А.Г. и др. - М.: Высшая школа, т.1,2, 2006-304с, 416с.
4 Кремер Н.Ш. Высшая математика для экономистов.-М.: «Юнити», 1999.-471с.
