Б 2. Б.1. Математический анализ
Б 2. Б.1. Математический анализ
Направление подготовки (специальность)
Экономика
Методические указания и задания к контрольной работе
(заочная форма обучения)
Профиль подготовки (специализация, магистерская программа)
Экономика предприятий и организаций
Бухгалтерский учет, анализ и аудит
Финансы и кредит
Налоги и налогообложение
Квалификация (степень) выпускника
бакалавр
Уфа-2016
ООУДК 51
ББК 22.1
М 33
Рекомендовано к изданию решением заседания кафедры математики (протокол № 9 от 25 мая 2015 года) и методической комиссией механического факультета (протокол № 9 от 27 мая 2015 года )
Составитель: доцент кафедры математики Костенко Н.А.
Рецензент: доцент кафедры бухгалтерского учета и аудита Насырова А.Д.
Ответственный за выпуск: зав. кафедрой математики доцент Лукманов Р.Л.
Оглавление
| Введение | ||
| Общие методические указания | ||
| Тема 1 Введение в анализ | ||
| Тема 2 Производная и дифференциал | ||
| Тема 3 Приложения производной | ||
| Тема 4 Функции нескольких переменных 4.1 Частные производные функции нескольких переменных 4.2 Экстремум функции нескольких переменных 4.3 Градиент. Производная по направлению | ||
| Тема 5 Неопределенный интеграл 5.1 Метод замены переменного 5.2 Метод интегрирования по частям 5.3 Интегрирование выражений, содержащих квадратный трехчлен 5.4 Интегрирование рациональных дробей | ||
| Тема 6 Определенный интеграл | ||
| Задания для контрольной работы | ||
| Литература | ||
Введение
Настоящие методические указания предназначены для студентов-заочников экономического направления (бакалавриат) Башкирского государственного аграрного университета.
Методические указания содержат общие рекомендация по изучению дисциплины «Математический анализ», краткие указания к выполнению контрольных работ, образцы решения некоторых задач, контрольные задания.
Задачи изучения курса математики вытекают из требований ФГОСа и квалификационной характеристики выпускника, который должен уметь:
- строить простейшие математические модели экономических задач;
- выбрать нужный метод для решения этих задач и решать эти задачи;
-уметь выработать на основе полученных решений практические рекомендации.
Целью данных методических указаний являются оказание теоретической и практической помощи студентам – заочникам (бакалаврам) в выполнении контрольной работы, в усвоении теоретического материала дисциплины и в подготовке к сдаче итогового испытания.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях.
Номер варианта по каждому заданию студент выбирает по формуле Ni=ab+c,
где Ni – номер варианта,
a - номер задания,
b - предпоследняя цифра шифра студента,
c - последняя цифра шифра
Пример. Пусть шифр студента 1235, тогда:
Номер варианта первого задания: N1=1×3+5=8;
Номер варианта второго задания N2=2×3+5=11;
Номер варианта третьего задания N3=3×3+5=14;
Номер варианта четвертого задания N4=4×3+5=17.
Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
Если итоговая цифра по формуле получится число больше 20, то для определения варианта от полученной цифры отнимают 20.
Пример. Путь шифр студента 1298.
Номер варианта второго здания: N2=2×9+9=26. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
Общие методические указания
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом: чтение учебников, решение задач, выполнение контрольных заданий.
Если в процессе изучения материала или при решении задач у студента возникают трудности, то можно обратиться к. преподавателю кафедры математики для получения устной, или письменной консультации. В случае письменной консультации студент должен точно указать характер затруднения, полное название учебника или задачника, год издания и страницу, где находится непонятный для студента вопрос или задача.
При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тет-ради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, номер контрольной работы, дата ее отсылки в институт, домашний адрес студента.
2. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условие.
3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.
4. Решение, задач геометрического содержания должно сопровождаться чертежами (желательно на миллиметровой бумаге), выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах.
5. На каждой странице тетради, необходимо оставлять поля шириной 3 — 4см для замечаний преподавателя.
6. Контрольные работы должны, выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена.
Изучите теорию по указанным разделам, разберите решения задач, приведенных в данных методических указаниях и приступайте к выполнению контрольных работ. Желаем удачи!
Тема 1 Введение в анализ
Разберите решение задач 1, 2 данного пособия.
Задача 1. Вычислить пределы:
a) 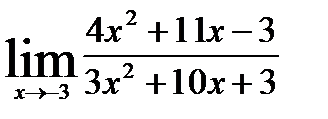 , б)
, б) 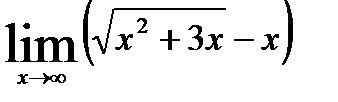
в). 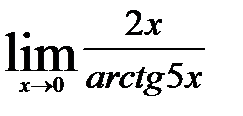 г)
г) 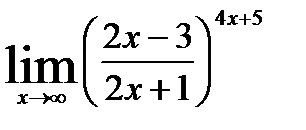
Решение. a) Подстановка предельного значения аргумента х= -3 приводит кнеопределенному выражению вида 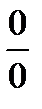 . Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при
. Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при 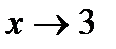 :
:
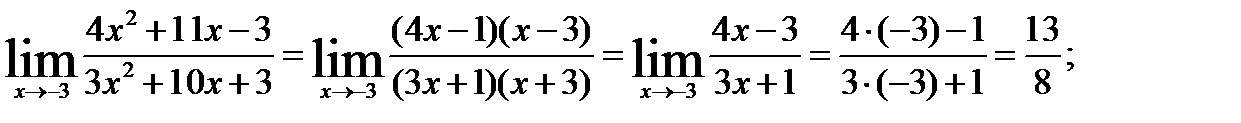
б). При 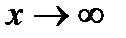 выражение
выражение 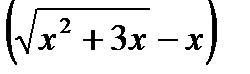 дает неопределенность вида
дает неопределенность вида 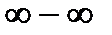 . Для ее устранения умножим и разделим это выражение на
. Для ее устранения умножим и разделим это выражение на 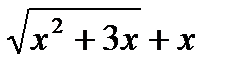
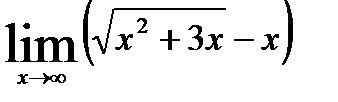 =
= 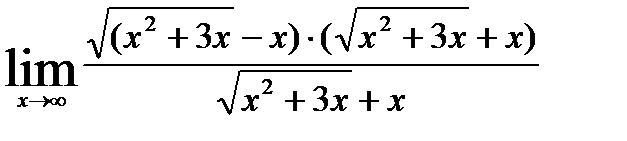 =
= 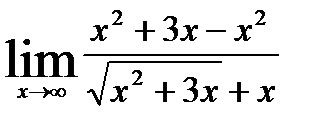 =
= 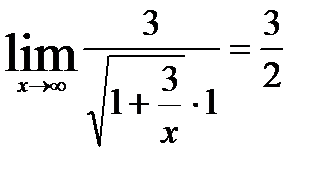 ;
;
в). Обозначим arctg5x=y. Тогда 5x=tg y и 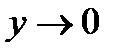 при
при 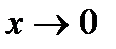 . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела 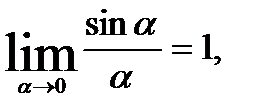 имеем:
имеем:
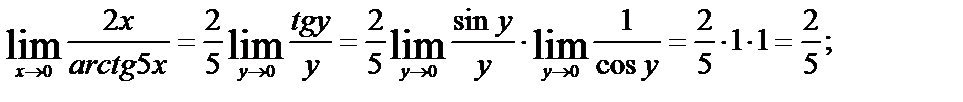
г). При 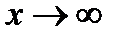 выражается
выражается 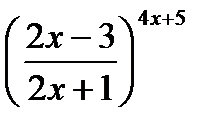 является неопределенностью вида
является неопределенностью вида 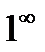 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при 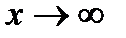 величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела: 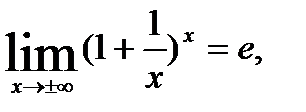
тогда имеем: 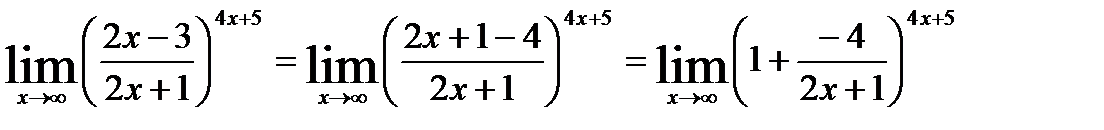
Пусть 2x+1=-4y. Тогда 4x+5=-8y+3 и 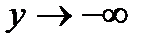 при
при 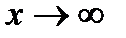 . Переходя к переменной y, получим:
. Переходя к переменной y, получим:
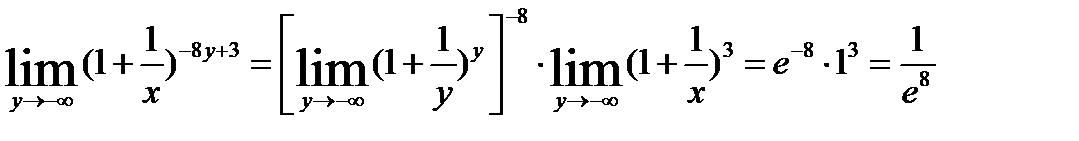
Задача 2. Исследовать на непрерывность функцию 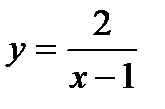 .
.
Решение. Данная функция является элементарной. Известно, что всякая элемен-тарная функция непрерывна на своей области определения. Данная функция определена на интервалах ( - 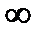 ; 1) и (1;
; 1) и (1; 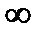 ) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 1.
) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 1.
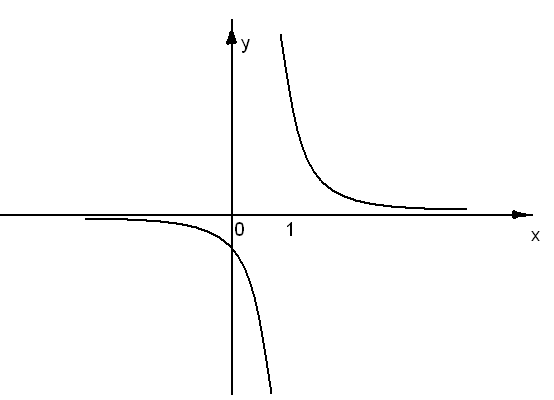
Рис. 1
Вопросы для самопроверки
1. Сформулируйте определение понятия функции.
2. Что называется областью определения функции? Областью изменения функции?
3. Перечислите основные элементарные функции. Назовите их основные свойства.
4. Какие функции называются элементарными? Приведите примеры.
5. Что называется пределом числовой последовательности?
6. Сформулируйте определение предела функции.
7. Назовите основные свойства пределов функций.
8. Какая функция называется бесконечно малой? Бесконечно большой?
9. Назовите свойства бесконечно малых функций.
10. Напишите формулы первого и второго замечательных пределов.
11. Какие логарифмы называются натуральными?
12. Дайте определение односторонних пределов функции в точке.
13. Какая функция называется непрерывной в точке? На интервале?
14. Какая точка называется точкой разрыва первого рода? Второго рода?
15. Перечислите основные свойства непрерывных на отрезке функций.
Литература
1 Письменный Д.Т. Конспект лекций по высшей математике (ч. 1,2)./Письменный Д.Т.-М.:«Айрис-пресс»,2007.-282с., 253с.
2 Лунгу К.Н. Сборник задач по высшей математике.(ч.1,2) -М.: «Айрис - пресс», 2008-574с.
Дополнительная литература
1 Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие / Н.С. Пискунов. –М.: Интеграл-Пресс. -2007.Ч.1. -415с.
2 Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие / Н.С. Пискунов. –М.: Интеграл-Пресс. -2006. Ч.2.-544с.
3 Данко П.Е., Попов А.Г. Высшая математики в упражнениях и задачах. / Данко П.Е. Попов А.Г. и др. - М.: Высшая школа, т.1,2, 2006-304с, 416с.
4 Кремер Н.Ш. Высшая математика для экономистов.-М.: «Юнити», 1999.-471с.
Б 2. Б.1. Математический анализ
Направление подготовки (специальность)
Экономика
Методические указания и задания к контрольной работе
(заочная форма обучения)
Профиль подготовки (специализация, магистерская программа)
Экономика предприятий и организаций
Бухгалтерский учет, анализ и аудит
Финансы и кредит
Налоги и налогообложение
Квалификация (степень) выпускника
бакалавр
Уфа-2016
ООУДК 51
ББК 22.1
М 33
Рекомендовано к изданию решением заседания кафедры математики (протокол № 9 от 25 мая 2015 года) и методической комиссией механического факультета (протокол № 9 от 27 мая 2015 года )
Составитель: доцент кафедры математики Костенко Н.А.
Рецензент: доцент кафедры бухгалтерского учета и аудита Насырова А.Д.
Ответственный за выпуск: зав. кафедрой математики доцент Лукманов Р.Л.
Оглавление
| Введение | ||
| Общие методические указания | ||
| Тема 1 Введение в анализ | ||
| Тема 2 Производная и дифференциал | ||
| Тема 3 Приложения производной | ||
| Тема 4 Функции нескольких переменных 4.1 Частные производные функции нескольких переменных 4.2 Экстремум функции нескольких переменных 4.3 Градиент. Производная по направлению | ||
| Тема 5 Неопределенный интеграл 5.1 Метод замены переменного 5.2 Метод интегрирования по частям 5.3 Интегрирование выражений, содержащих квадратный трехчлен 5.4 Интегрирование рациональных дробей | ||
| Тема 6 Определенный интеграл | ||
| Задания для контрольной работы | ||
| Литература | ||
Введение
Настоящие методические указания предназначены для студентов-заочников экономического направления (бакалавриат) Башкирского государственного аграрного университета.
Методические указания содержат общие рекомендация по изучению дисциплины «Математический анализ», краткие указания к выполнению контрольных работ, образцы решения некоторых задач, контрольные задания.
Задачи изучения курса математики вытекают из требований ФГОСа и квалификационной характеристики выпускника, который должен уметь:
- строить простейшие математические модели экономических задач;
- выбрать нужный метод для решения этих задач и решать эти задачи;
-уметь выработать на основе полученных решений практические рекомендации.
Целью данных методических указаний являются оказание теоретической и практической помощи студентам – заочникам (бакалаврам) в выполнении контрольной работы, в усвоении теоретического материала дисциплины и в подготовке к сдаче итогового испытания.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях.
Номер варианта по каждому заданию студент выбирает по формуле Ni=ab+c,
где Ni – номер варианта,
a - номер задания,
b - предпоследняя цифра шифра студента,
c - последняя цифра шифра
Пример. Пусть шифр студента 1235, тогда:
Номер варианта первого задания: N1=1×3+5=8;
Номер варианта второго задания N2=2×3+5=11;
Номер варианта третьего задания N3=3×3+5=14;
Номер варианта четвертого задания N4=4×3+5=17.
Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
Если итоговая цифра по формуле получится число больше 20, то для определения варианта от полученной цифры отнимают 20.
Пример. Путь шифр студента 1298.
Номер варианта второго здания: N2=2×9+9=26. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
Общие методические указания
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом: чтение учебников, решение задач, выполнение контрольных заданий.
Если в процессе изучения материала или при решении задач у студента возникают трудности, то можно обратиться к. преподавателю кафедры математики для получения устной, или письменной консультации. В случае письменной консультации студент должен точно указать характер затруднения, полное название учебника или задачника, год издания и страницу, где находится непонятный для студента вопрос или задача.
При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тет-ради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, номер контрольной работы, дата ее отсылки в институт, домашний адрес студента.
2. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условие.
3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.
4. Решение, задач геометрического содержания должно сопровождаться чертежами (желательно на миллиметровой бумаге), выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах.
5. На каждой странице тетради, необходимо оставлять поля шириной 3 — 4см для замечаний преподавателя.
6. Контрольные работы должны, выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена.
Изучите теорию по указанным разделам, разберите решения задач, приведенных в данных методических указаниях и приступайте к выполнению контрольных работ. Желаем удачи!
Тема 1 Введение в анализ
Разберите решение задач 1, 2 данного пособия.
Задача 1. Вычислить пределы:
a) 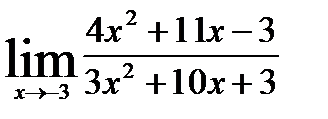 , б)
, б) 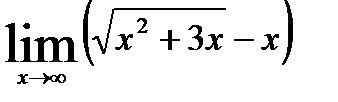
в). 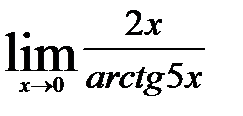 г)
г) 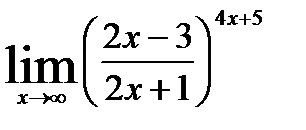
Решение. a) Подстановка предельного значения аргумента х= -3 приводит кнеопределенному выражению вида 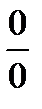 . Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при
. Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при 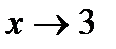 :
:
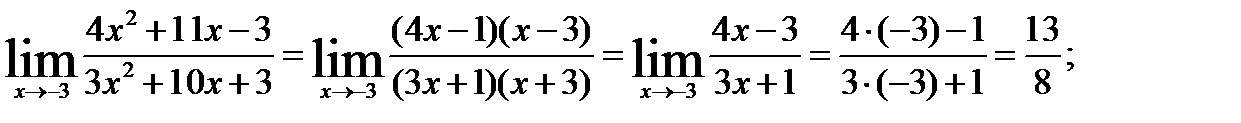
б). При 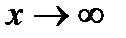 выражение
выражение 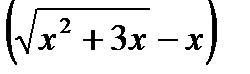 дает неопределенность вида
дает неопределенность вида 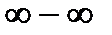 . Для ее устранения умножим и разделим это выражение на
. Для ее устранения умножим и разделим это выражение на 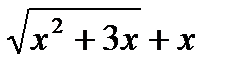
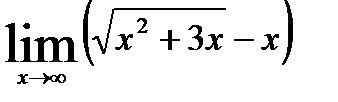 =
= 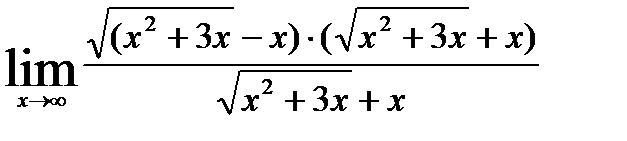 =
= 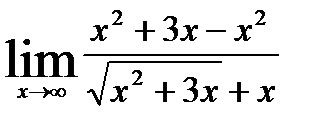 =
= 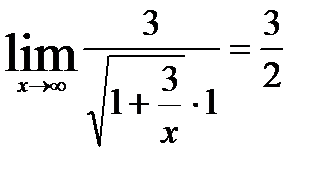 ;
;
в). Обозначим arctg5x=y. Тогда 5x=tg y и 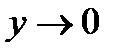 при
при 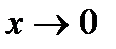 . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела 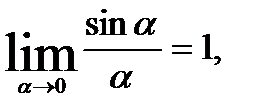 имеем:
имеем:
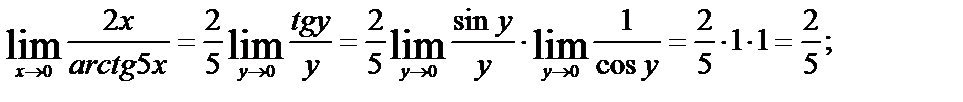
г). При 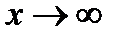 выражается
выражается 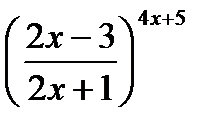 является неопределенностью вида
является неопределенностью вида 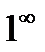 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при 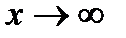 величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела: 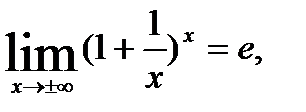
тогда имеем: 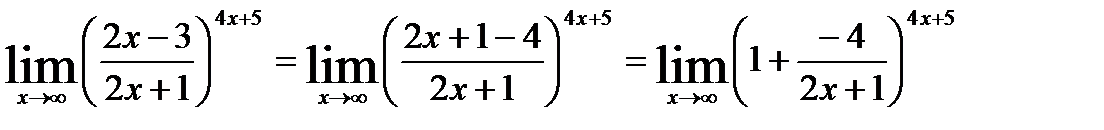
Пусть 2x+1=-4y. Тогда 4x+5=-8y+3 и 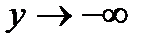 при
при 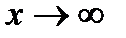 . Переходя к переменной y, получим:
. Переходя к переменной y, получим:
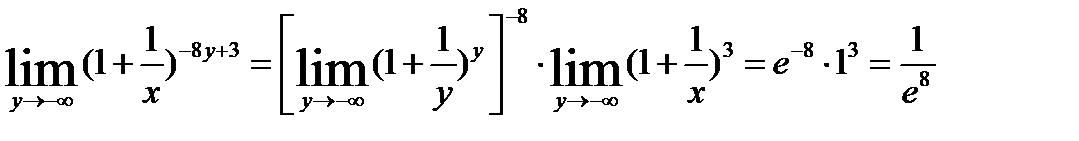
Задача 2. Исследовать на непрерывность функцию 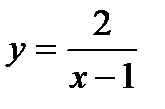 .
.
Решение. Данная функция является элементарной. Известно, что всякая элемен-тарная функция непрерывна на своей области определения. Данная функция определена на интервалах ( - 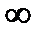 ; 1) и (1;
; 1) и (1; 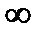 ) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 1.
) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 1.

Рис. 1
Вопросы для самопроверки
1. Сформулируйте определение понятия функции.
2. Что называется областью определения функции? Областью изменения функции?
3. Перечислите основные элементарные функции. Назовите их основные свойства.
4. Какие функции называются элементарными? Приведите примеры.
5. Что называется пределом числовой последовательности?
6. Сформулируйте определение предела функции.
7. Назовите основные свойства пределов функций.
8. Какая функция называется бесконечно малой? Бесконечно большой?
9. Назовите свойства бесконечно малых функций.
10. Напишите формулы первого и второго замечательных пределов.
11. Какие логарифмы называются натуральными?
12. Дайте определение односторонних пределов функции в точке.
13. Какая функция называется непрерывной в точке? На интервале?
14. Какая точка называется точкой разрыва первого рода? Второго рода?
15. Перечислите основные свойства непрерывных на отрезке функций.
