Неустановившееся движение электропривода
Неустановившееся движение ЭП имеет место, когда моменты двигателя и нагрузки отличаются друг от друга, т.е. 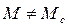 . В этом случае динамический момент
. В этом случае динамический момент 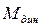 не равен нулю и происходит изменение скорости движения (пуск, торможение, реверс, изменение нагрузки на валу).
не равен нулю и происходит изменение скорости движения (пуск, торможение, реверс, изменение нагрузки на валу).
Неустановившееся движение характеризует переходный процесс. Переходный процесс в системе ЭП позволяет установить зависимость механических переменных (координат) ЭП: моментов, скорости, угла поворота вала двигателя от времени - и оценить динамику привода.
На динамику ЭП влияет множество факторов, основными из которых являются механическая инерция частей ЭП и электромагнитная инерция электрических цепей. В тех случаях, когда механическая инерция является определяющей, модель ЭП строят из учета только механических процессов, определяемых уравнением движения ЭП. И исходя из этого, переходные процессы называются механическими. Когда влияние электромагнитных процессов достаточно велико, то учитывают электромагнитные процессы в электрических цепях, при этом определяют иногда не одну, а несколько постоянных времени. Учет электромагнитных процессов значительно усложняет расчет ЭП, и полученная в результате рассмотрения система называется электромеханической. Чаще всего она нелинейна, и линеаризация ее возможна лишь на отдельных участках.
В некоторых случаях приходится учитывать и тепловую инерцию, имеющую место в электромашинных установках. Она, как правило, учитывается в установках с малоинерционными ЭД. У этих ЭД в переходных процессах допустимы очень большие токи, которые вызывают быстрый нагрев обмоток, расположенных вне стальных сердечников. Поэтому возникает необходимость в ограничении токов с одной стороны и в учете изменений параметров ЭД в переходных режимах с другой стороны.
Другой особенностью ЭП является необходимость рассматривать систему часто при одновременном действии управляющего и возмущающего воздействий. То есть, рассматривая переходные процессы по управлению, приходится обязательно учитывать нагрузку привода. Статический момент на валу РМ может носить достаточно сложный характер. Он может зависеть от скорости, времени, угла поворота и других факторов. Его зависимость от скорости не всегда удается выразить в аналитической форме, и поэтому приходится рассматривать идеализированные модели. Тем не менее, существует большая группа машин, у которых статический момент постоянный 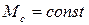 . Это характерно для машин, статическая нагрузка которых в основном определяется трением, а также для машин с активным статическим моментом (подъемно-транспортные устройства). Кроме трения при рассмотрении нагрузки возникает необходимость учитывать сопротивление движению механизма со стороны воздуха. В этом случае момент сопротивления пропорционален скорости
. Это характерно для машин, статическая нагрузка которых в основном определяется трением, а также для машин с активным статическим моментом (подъемно-транспортные устройства). Кроме трения при рассмотрении нагрузки возникает необходимость учитывать сопротивление движению механизма со стороны воздуха. В этом случае момент сопротивления пропорционален скорости
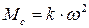 .
.
Учитывая квадратичный характер, такую нагрузку называют вентиляторной. Учет такой нагрузки приводит к получению нелинейных дифференциальных уравнений, что значительно усложняет расчет. Поэтому на практике часто для того, чтобы оценить влияние сопротивления воздуха (внешнее скоростное трение), полагают для упрощения, что
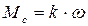 .
.
Естественно, возможен случай и при наличии двух составляющих статического момента
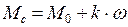 ,
,
где 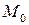 - постоянная составляющая.
- постоянная составляющая.
Иногда приходится рассматривать механизмы с неуравновешенными массами, кривошипно-шатунными передачами, муфтами, в которых момент сопротивления является функцией угла поворота
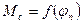 .
.
В некоторых случаях приходится рассматривать зависимость момента от времени
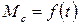 .
.
Статический момент сопротивления может носить и случайный характер, и тогда используются статистические методы анализа.
Рассмотрим несколько простейших, широко встречающихся на практике случаев:
Механические переходные режимы [9].
1 случай. 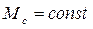 .
.
Пусть 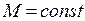 (рис. 2.8), в этом случае уравнение движения (2.11) решается методом разделения переменных и его решение имеет вид при постоянной интегрирования
(рис. 2.8), в этом случае уравнение движения (2.11) решается методом разделения переменных и его решение имеет вид при постоянной интегрирования 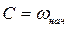
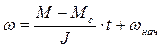 , (2.15)
, (2.15)
где 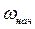 - начальное значение скорости при t=0.
- начальное значение скорости при t=0.
Как видим, скорость ω линейно зависит от времени, момент двигателя М от времени не зависит. Из решения уравнения движения определим время переходного процесса tпп при изменении скорости от 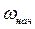 до
до 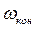
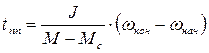 . (2.16)
. (2.16)
Скорость изменяется по линейному закону, и если 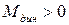 , то имеем разгон, а если
, то имеем разгон, а если 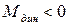 , то замедление.
, то замедление.
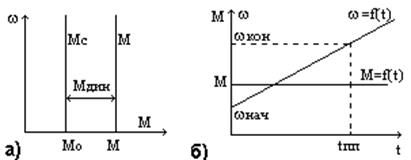 |
Рис. 2.8. Механические характеристики (а) и переходная характеристика (б) регулируемого электропривода.
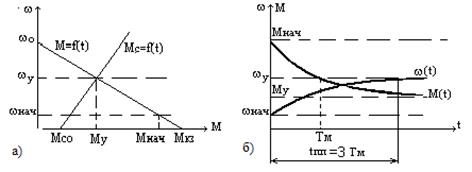
2 случай.Моменты РМ и ЭД линейно зависят от скорости (рис. 2.9):
Мс=Мс0 + βс∙ω, (2.17)
М=Мкз - β∙ω,(2.18)
где 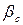 - жесткость механической характеристики РМ;
- жесткость механической характеристики РМ;
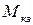 - момент короткого замыкания двигателя;
- момент короткого замыкания двигателя;
 |
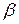 - жесткость механической характеристики ДПТ НВ.
- жесткость механической характеристики ДПТ НВ. Рис. 2.9. Механические характеристики (а) и переходные процессы (б)
электропривода
Подставляя уравнения моментов (2.17) и (2.18) в уравнение движения (2.11), получим:
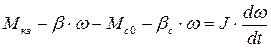 , или
, или
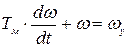 , (2.19)
, (2.19)
где 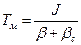 - электромеханическая постоянная времени, с;
- электромеханическая постоянная времени, с;
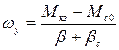 - установившаяся скорость, соответствующая точке пересечения механических характеристик ЭД и РМ, рад/с.
- установившаяся скорость, соответствующая точке пересечения механических характеристик ЭД и РМ, рад/с.
Решая дифференциальное уравнение (2.19), определим изменение скорости: 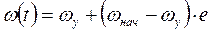 -t/Tм (2.20)
-t/Tм (2.20)
где ( 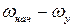 )=А - постоянная интегрирования.
)=А - постоянная интегрирования.
В данном случае при линейных характеристиках и линейно изменяющемся динамическом моменте частота вращения ЭП изменяется по экспоненте от 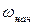 до
до 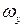 .
.
Имея закон изменения скорости, можно написать закон изменения моментов. Запишем момент двигателя в функции времени из (2.18)
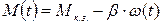 ,
,
с учетом того, что
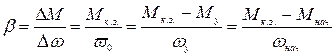
получим
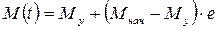 -t/Tм. (2.21)
-t/Tм. (2.21)
На практике часто встречается случай, когда 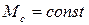 , то есть
, то есть 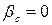 .
.
Тогда 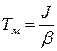 , и учитывая, что
, и учитывая, что 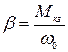 , получим:
, получим:
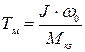 . (2.22)
. (2.22)
Из полученных ранее дифференциальных уравнений легко можно определить время переходного процесса, за которое скорость меняется от 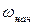 до
до 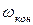 и момент от
и момент от 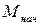 до
до 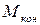 . При этом:
. При этом:
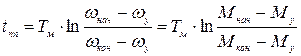 . (2.23)
. (2.23)
Очевидно, что при линейных характеристиках и частота вращения, и момент изменяются по экспоненте с постоянной времени 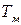 . Начальные и установившиеся значения частоты вращения и момента определяются из установившегося режима работы ЭП.
. Начальные и установившиеся значения частоты вращения и момента определяются из установившегося режима работы ЭП.
3 случай.Произвольно изменяющийся динамический момент.
В общем случае моменты ЭД и РМ могут быть различными, в том числе и нелинейными, функциями скорости, времени или положения. Тогда зависимости  и
и  получить довольно сложно, так как уравнение движения в этом случае не имеет единого решения. Возможны несколько направлений решения задачи:
получить довольно сложно, так как уравнение движения в этом случае не имеет единого решения. Возможны несколько направлений решения задачи:
1. Линеаризация нелинейных характеристик ЭД и РМ. В этом случае удается использовать полученные ранее выражения;
2. Точное интегрирование уравнения движения. Это возможно лишь тогда, когда характеристики ЭД и РМ заданы аналитически как функции скорости, положения или времени;
3. Чаще всего характеристики ЭД и РМ заданы или графически или таблично. В этих случаях используют обычно методы численного интегрирования;
4. Графоаналитические методы построения кривых переходного процесса. Эти методы используются тогда, когда характеристики заданы графически. Графоаналитические методы просты, наглядны и позволяют получить достаточную точность. В теории ЭП разработано несколько таких методов (метод площадей, пропорций). В основе этих методов лежит также решение уравнения движения.
