Синтез систем подчиненного регулирования
Рассмотрим синтез системы стабилизации скорости вращения ДПТ НВ [2, 4, 5, 11].
Исходная структурная схема разомкнутой системы представлена на рис. 2.14.
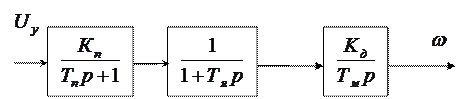 |
Рис. 2.14. Структурная схема разомкнутой системы
Главная задача в этом случае – регулирование частоты вращения, и, следовательно, наружный контур будет контуром скорости. В качестве внутреннего выделим контур тока (рис. 2.15).
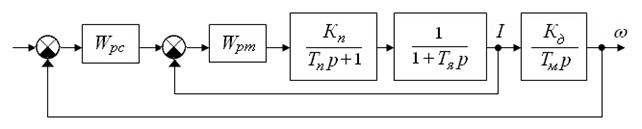
Рис.2.15. Структурная схема регулирования скорости
Синтез системы начинают с внутреннего контура (рис. 2.16).
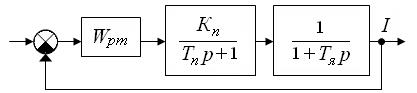
Рис.2.16. Структурная схема внутреннего контура тока.
Передаточная функция объекта регулирования во внутреннем контуре:
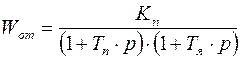 .
.
Так как 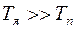 , задача при выборе регулятора будет состоять в том, чтобы скомпенсировать большую постоянную времени контура; считаем, что
, задача при выборе регулятора будет состоять в том, чтобы скомпенсировать большую постоянную времени контура; считаем, что 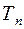 малая некомпенсируемая постоянная времени (
малая некомпенсируемая постоянная времени ( 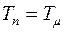 ). Очевидно, чтобы получить в результате введения регулятора интегрирующее звено, регулятор должен иметь передаточную функцию вида:
). Очевидно, чтобы получить в результате введения регулятора интегрирующее звено, регулятор должен иметь передаточную функцию вида:
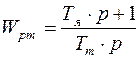
Тогда результирующая передаточная функция прямой цепи будет: 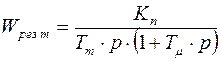 .
.
Расчет ведем на технический оптимум, таким образом 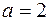 . Принимаем
. Принимаем 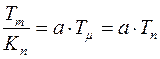 .
.
Запишем передаточную функцию в следующем виде: 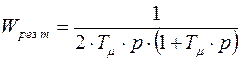 .
.
Определим передаточную функцию замкнутого контура тока: 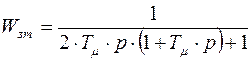 .
.
Если раскрыть скобки в знаменателе, то получим член с 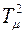 ; учитывая, что
; учитывая, что 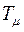 малая величина, этим членом часто пренебрегают. Тогда:
малая величина, этим членом часто пренебрегают. Тогда: 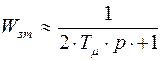 .
.
Определив таким образом передаточную функцию регулятора тока, переходим к синтезу регулятора скорости, то есть к расчету наружного контура системы. Наружный контур можно представить в следующем виде (рис. 2.17):
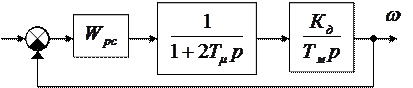 |
Рис.2.17. Структурная схема наружного контура скорости
Очевидно, что в данном случае величина 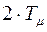 в знаменателе может считаться малой некомпенсируемой постоянной времени уже наружного контура.
в знаменателе может считаться малой некомпенсируемой постоянной времени уже наружного контура.
Передаточная функция объекта регулирования может быть записана для внешнего контура в следующем виде:
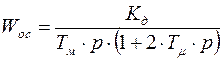 .
.
Так как 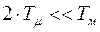 , задача состоит в том, чтобы скомпенсировать большую постоянную времени
, задача состоит в том, чтобы скомпенсировать большую постоянную времени 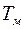 . Для этого достаточно ввести в контур пропорциональный регулятор с передаточной функцией:
. Для этого достаточно ввести в контур пропорциональный регулятор с передаточной функцией: 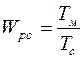 и тогда передаточная функция прямой цепи будет иметь вид:
и тогда передаточная функция прямой цепи будет иметь вид:
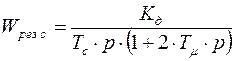 .
.
Так как 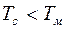 . Выберем
. Выберем 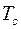 из следующего условия:
из следующего условия: 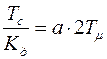 , где
, где 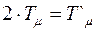 - малая некомпенсируемая постоянная времени наружного контура. Полагая
- малая некомпенсируемая постоянная времени наружного контура. Полагая 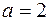 , будем иметь
, будем иметь 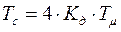 . В результате передаточная функция замкнутой системы:
. В результате передаточная функция замкнутой системы:
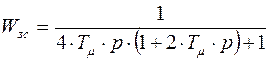 .
.
Характеристическое уравнение:
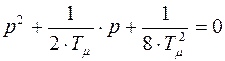 .
.
Собственная частота всей системы 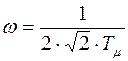 , а коэффициент демпфирования λ =
, а коэффициент демпфирования λ = 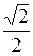 . Таким образом перерегулирование переходного процесса будет составлять
. Таким образом перерегулирование переходного процесса будет составлять 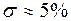 .
.
Использование данной методики позволяет практически независимо рассчитывать параметры каждого регулятора.
При переходе от внутреннего контура к наружному при одном и том же значении 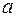 малая некомпенсируемая постоянная времени будет в
малая некомпенсируемая постоянная времени будет в 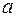 раз больше у внешнего контура, чем у внутреннего. Система, у которой
раз больше у внешнего контура, чем у внутреннего. Система, у которой 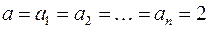 , рассматривается как система, настроенная на модульный (технический) оптимум. Такая настройка наиболее часто используется на практике. При
, рассматривается как система, настроенная на модульный (технический) оптимум. Такая настройка наиболее часто используется на практике. При 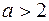 получаем систему с меньшим быстродействием, переходный процесс которой приближается к апериодическому.
получаем систему с меньшим быстродействием, переходный процесс которой приближается к апериодическому.
Рассмотренная система (рис.2.15) содержит только один интегрирующий регулятор, то есть она обладает свойствами астатической системы с астатизмом первого порядка. В тех случаях, когда необходимо исключить и скоростную ошибку, вводят еще один интегрирующий регулятор, так называемый регулятор ускорения (рис.2.18).

Рис.2.18. Структурная схема системы регулирования
с астатизмом второго порядка
Из вышеприведенного примера:
передаточная функция замкнутого контура тока 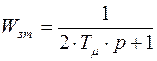 ,
,
передаточная функция регулятора ускорения: 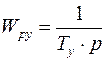 .
.
Цепь обратной связи датчика ускорения подключаем к датчику тока, так как при отсутствии статической нагрузки ускорение пропорционально току якорной цепи.
При 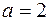 ,
, 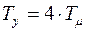 ,
,
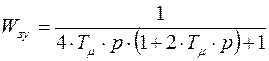 .
.
Пренебрегая 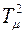 , получим:
, получим: 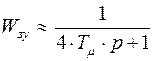 .
.
Результирующая передаточная функция разомкнутой цепи контура скорости:
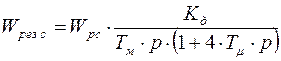 .
.
Очевидно, что для компенсации 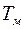 необходимо, чтобы
необходимо, чтобы 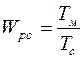 , то есть имеем пропорциональный регулятор скорости. Подставляя это выражение в передаточную функцию, получим:
, то есть имеем пропорциональный регулятор скорости. Подставляя это выражение в передаточную функцию, получим:
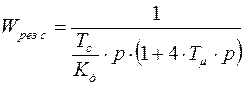 .
.
Учитывая, что настройка идет на технический оптимум, то есть 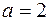 , получим:
, получим:
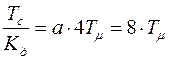 .
.
В результате передаточная функция замкнутой системы с астатизмом второго порядка будет иметь вид:
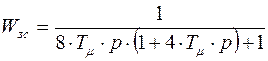 .
.
Характеристическое уравнение: 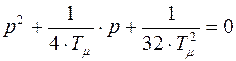 .
.
Собственная частота всей системы 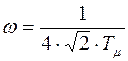 .
.
Коэффициент демпфирования λ = 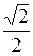 .
.
В данной системе за счет двух интегрирующих регуляторов исключается скоростная ошибка.
В тех случаях, когда есть необходимость уменьшить количество контуров, применяют искусственный прием преобразования структурных схем. Рассмотренную выше трехконтурную систему, используя метод преобразования, можно представить как двухконтурную (рис.2.19).

Рис.2.19. Преобразованная структурная схема системы регулирования
с астатизмом второго порядка
При этом: 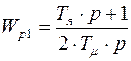 ,
, 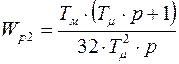 ,
, 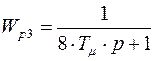 .
.
Обычно системы подчиненного регулирования имеют не более трех контуров. Так в следящих системах внешний контур – контур регулирования угла поворота, средний контур – контур скорости, а внутренний – контур тока.
