Разработка структурной схемы линейной нейронной сети.

Линейная сеть, которая показана на рисунке 7.3. а) включает 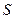нейронов, которые размещены в одном слое и связанных с 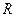входами через матрицу весов 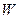. На рисунке 7.3.б) изображена укрупненная структурная схема этой сети, вектор выхода 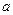, который имеет размер .

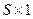Разработка алгоритма создания и моделирования линейной нейронной сети.

Линейную сеть с одним нейроном, которая показана на рисунке 7.1, можно создать следующим образом: 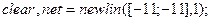Первый входной аргумент задает диапазон изменения элементов вектора входа; второй аргумент указывает, что сеть имеет единственный выход. Начальные веса и смещение по умолчанию равны нулю.

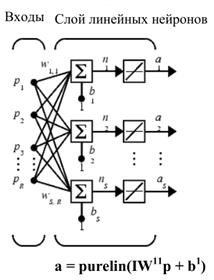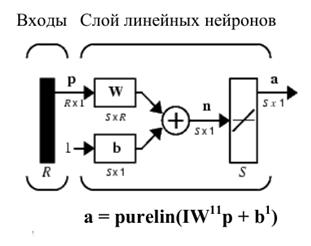а)	б)
Рисунок 7.3.

Определение параметров созданной нейронной сети.Присвоим весам и смещению следующие значения: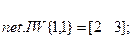

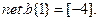
Промоделируем линейную сеть вектора входа:

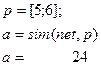
Таким образом, сеть правильно классифицировала входной вектор.

Порядок выполнения работы

1. Разработать структурную схему линейной нейронной сети варианты задания в таблице 7.1.

Таблица 7.1

Номер варианта	Количество входов	Диапазоны значений входов	Количество нейронов в слое
1.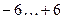
2.
3.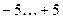
4.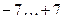
5.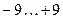
6.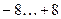
7.
8.
9.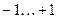
10.

2. Разработать алгоритм создания и моделирования линейной нейронной сети.

3. Реализовать разработанный алгоритм в программе .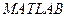

4. Определить параметры созданной нейронной сети: веса и смещение. Проверить правильность работы сети для последовательности входных векторов (не менее 5).

5. Построить график, аналогичный изображенному рисунку 5.2, для своих исходных данных.

6. Определить имя функции инициализации значений матриц весов и смещений, принятой по умолчанию для линейных нейронных сетей. Установить новые значения матриц весов и смещения с помощью функции инициализации .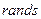

7. Распечатать листинг программы.

8. Составить отчет: цель практического занятия, структурную схему нейронной сети, алгоритм, текст программы и график, выводы.

Практическое занятие №8

Обучение и настройка линейной сети

Цель работы:

- Процедура настройки посредством прямого расчета.

- Построение графиков для получения значений веса и смещения, поверхности функции ошибки.

Теоретическая часть

Линейные сети способны решать линейно отделимые задачи классификации. В них используется правило обучение, основанное на методе обучения наименьших квадратов, которое является более мощным, чем правило обучения персептрона.

Для заданной линейной сети и соответствующего множества векторов входа и целей можно вычислить вектор выхода сети и сформировать разность между вектором и целевым вектором, которая определит некоторую погрешность.

В процессе обучения сети требуется найти такие значения весов и смещений, чтобы сумма квадратов соответствующих погрешностей была минимальной, поэтому настройка параметров выполняется таким образом, чтобы обеспечить минимум ошибки. Эта задача разрешима, так кА для линейной сети поверхность ошибки как функция входов единственный минимум, и отыскание этого минимума не вызывает трудностей.

Как и для персептрона, для линейной сети применяется процедура обучения с учителем, которая использует обучающее множества вида

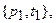
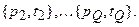(8.1)

Требуется минимизировать одну из следующих функций квадратичной ошибки:

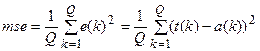(8.2)

или

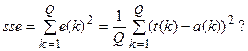(8.3)

где 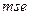- средняя квадратичная ошибка; 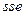- сумма квадратов ошибок.