Синтез нечетких алгоритмов управления на основе метода векторных функций Ляпунова
Цель работы
- Изучение метода синтеза систем управления типа Такаги-Сугено с формированием нечеткого логического регулятора с применением метода векторных функций.
- Рассмотреть системы управления общего вида, линейные и нелинейные системы.
- Исследование системы автоматического регулирования с нечетким регулятором.
Теоретические сведения
Предлагается метод синтеза нелинейных систем управления с запаздыванием типа Такаги-Сугено [3-5] с формированием нечеткого логического регулятора. В отличие от других работ рассматриваемый подход эффективно использует метод векторных функций Ляпунова (ВФЛ) [1,2]. Метод векторных функций Ляпунова (ВФЛ) [1] является точным и эффективным методом исследования систем управления. Нечеткая логическая система состоит из динамического процесса и нечеткого логического регулятора. Пусть 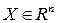 . Система управления характеризуется как нелинейная система с несколькими входами, моделируемой системой
. Система управления характеризуется как нелинейная система с несколькими входами, моделируемой системой
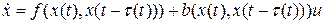 ,
, 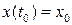 , (4.1)
, (4.1)
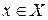 ,
, 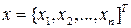 - вектор состояния;
- вектор состояния;
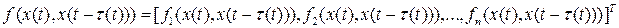 - нелинейный вектор,
- нелинейный вектор, 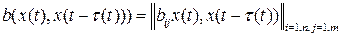 - матрица с нелинейными элементами, описывающие динамику системы управления;
- матрица с нелинейными элементами, описывающие динамику системы управления; 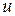 - управление, полученное дефазификацией методом центров тяжести для
- управление, полученное дефазификацией методом центров тяжести для 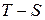 систем.
систем. 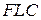 состоит из
состоит из 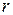 нечетких
нечетких 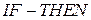 правил. Правило в
правил. Правило в 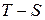 системе записывается в виде
системе записывается в виде
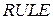
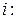
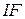
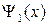
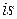
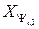
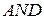 …
… 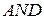
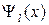
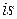
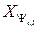
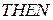
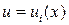 ,
, 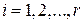 ;
; 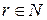 , (4.2)
, (4.2)
где 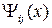 ,
, 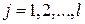 нечеткие множества,
нечеткие множества, 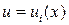 -управление, определяемое
-управление, определяемое 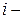 м правилом.
м правилом.
Каждое нечеткое правило генерирует 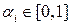 ,
, 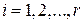 , согласно
, согласно
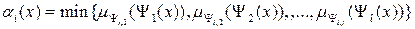 - функции принадлежности.
- функции принадлежности.
Управление 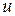 , которое должно быть применено в процессе, является функцией
, которое должно быть применено в процессе, является функцией 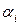 и
и 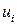 . Выход
. Выход 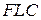 задается
задается 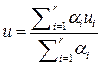 .
.
Пример 1. Системы управления общего вида.
Рассматривается система
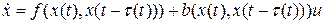 ,
, 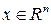 ,
, 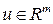 . (4.3)
. (4.3)
Согласно идеям метода ВФЛ строятся системы сравнения [1]. Здесь используются линейные системы сравнения (СС) [1] вида
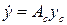 , (4.4)
, (4.4)
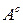 - постоянная матрица с известными свойствами [1] . Запишем ВФЛ
- постоянная матрица с известными свойствами [1] . Запишем ВФЛ 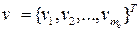 .
.
В данной работе полагаем 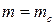 . Возможны другие варианты. Компоненты ВФЛ выбираем в виде квадратичных форм
. Возможны другие варианты. Компоненты ВФЛ выбираем в виде квадратичных форм 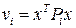 ,
, 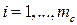 ,
, 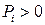 - симметричная положительно определенная матрица. Производная компонент ВФЛ в силу СУ имеет вид
- симметричная положительно определенная матрица. Производная компонент ВФЛ в силу СУ имеет вид
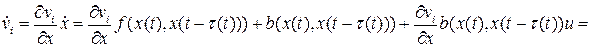
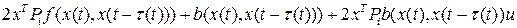
Или 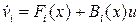 , где
, где 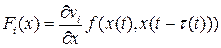
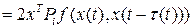 ,
, 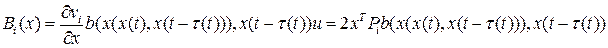 .
.
Определим множества по всем компонентам ВФЛ 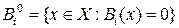 ,
, 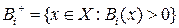 ,
, 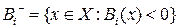 ,
, 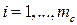 . Аналогичные выражения будем использовать и в других случаях, имеющих подобный смысл.
. Аналогичные выражения будем использовать и в других случаях, имеющих подобный смысл.
Из дифференциального неравенства [1] 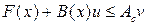 следует (см.[6])
следует (см.[6]) 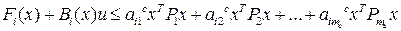 ; или
; или
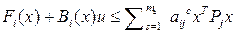 ,
, 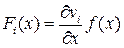 ,
, 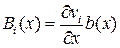 .
.
Преобразуем: 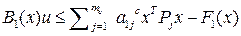 ,
, 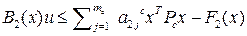 ,…,
,…, 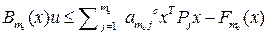 .
.
Дифференциальное неравенство запишется в следующем виде
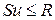 ,
,
где 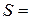
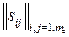 ,
, 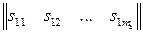 =
= 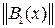 ,
, 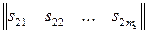 =
= 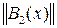 ,…,
,…, 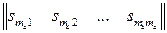 =
= 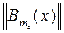 ,
, 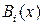 -вектор-строка
-вектор-строка 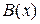 ,
, 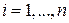 .
.
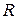 =
= 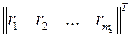 ,
, 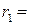
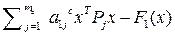 ;
; 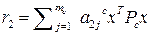 -
- 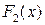 ; … ;
; … ;
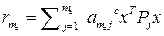 -
- 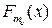 .
.
Если 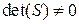 , управление выбирается из соотношения
, управление выбирается из соотношения 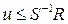 при
при 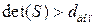 , где
, где 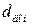 - фиксированное малое число. Вводится
- фиксированное малое число. Вводится 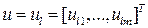 , - вспомогательное управление, согласованное с нечетким регулятором, чтобы не возникало особенностей. Если
, - вспомогательное управление, согласованное с нечетким регулятором, чтобы не возникало особенностей. Если 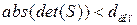 , в СУ необходимо дополнительно ввести такой линейный регулятор. Обозначим
, в СУ необходимо дополнительно ввести такой линейный регулятор. Обозначим 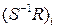 -
- 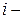 строку матрицы
строку матрицы 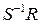 . Тогда при обозначении
. Тогда при обозначении 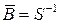 запишется
запишется
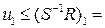
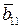 (
( 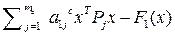 )+
)+ 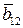 (
( 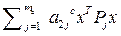 -
- 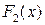 )
)
+…+ 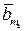 (
( 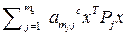 -
- 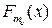 );
);
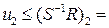
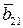 (
( 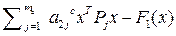 )+
)+ 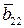 (
( 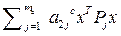 -
- 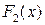 )
)
+…+ 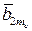 (
( 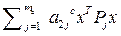 -
- 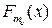 )
)
…
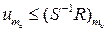 =
= 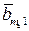 (
( 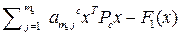 )+
)+ 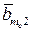 (
( 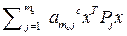 -
- 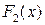 )
)
+…+ 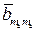 (
( 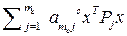 -
- 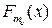 )
)
Воспользуемся частным случаем матрицы 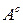 - диагональной матрицей
- диагональной матрицей 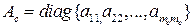 ,
, 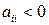 ,
, 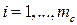 .
.
Тогда получим соотношение для синтеза регулятора
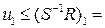
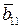 (
( 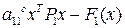 );
); 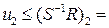
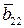 (
( 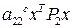 -
- 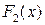 ); … ;
); … ;
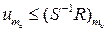 =
= 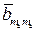 (
( 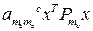 -
- 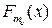 ).
).
Пример 2. Линейные системы.
Воспользуемся вспомогательной леммой [7]
Лемма [7 ]. Пусть 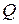 любая
любая 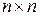 матрица. Для
матрица. Для 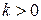 постоянной и симметричной матрицы
постоянной и симметричной матрицы 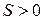 выполняется (
выполняется ( 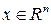 ,
, 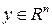 )
)
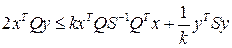
Пусть система имеет вид
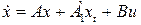 ,
, 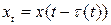 (4.4)
(4.4)
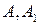 -
- 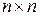 -,
-, 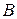 -
- 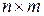 -постоянные матрицы.;
-постоянные матрицы.; 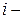 я компонента ВФЛ определяется выражением
я компонента ВФЛ определяется выражением 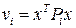 . Тогда с линейной СС можно записать дифференциальное неравенство
. Тогда с линейной СС можно записать дифференциальное неравенство
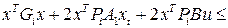
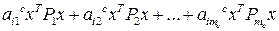 ,
,
где 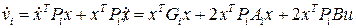 ,
, 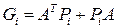 , ,
, , 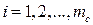 . Отсюда определяется система неравенств
. Отсюда определяется система неравенств
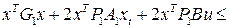
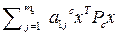 ,
, 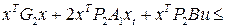
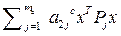 , …,
, …,
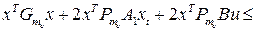
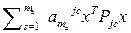
Перепишем неравенства в следующем виде
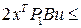
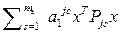 -
- 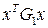
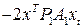 ,
, 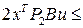
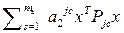 -
- 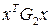
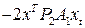 , … ,
, … , 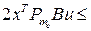
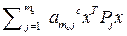 -
- 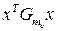
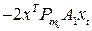 .
.
И используя лемму, преобразуем неравенства
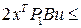
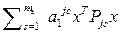 -
- 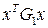 -
- 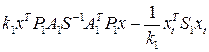 ,
, 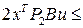
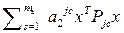 -
- 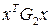 -
- 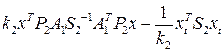 , …,
, …, 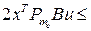
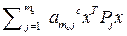 -
- 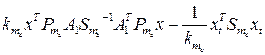
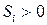 симметричная матрица,
симметричная матрица, 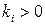 постоянная.
постоянная.
Еще раз перепишем с обозначениями 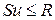 ,
, 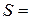

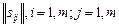 ,
, 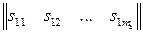 =
= 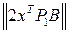 ,
, 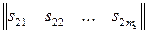 =
= 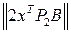 ,…,
,…, 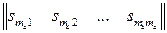 =
= 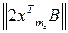 ,
, 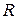 =
= 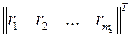 ,
, 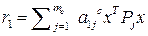 -
- 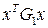 -
- 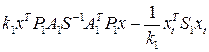 ;
; 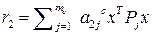 -
- 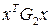 -
- 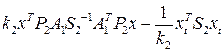 ;…;
;…; 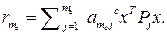 -
- 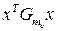 -
- 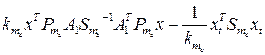 .
.
В общем случае матрица 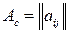 должна удовлетворять специальным свойствам [1]. Применим частный случай диагональной матрицы
должна удовлетворять специальным свойствам [1]. Применим частный случай диагональной матрицы 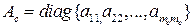 ,
, 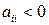 , получим
, получим
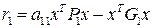 -
-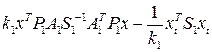 ;
; 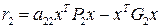 -
-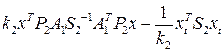 ;…;
;…; 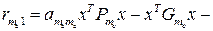
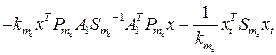 .
.
Теперь, аналогично, управление находится из 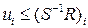 ,
, 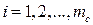 .
.
Замечание. Если матрица 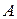 не является Гурвицевой, то возможен второй подход: алгоритм начинается с задания ВФЛ. Первый эффективно алгоритмизируется. При втором необходимо детально рассматривать особенности системы управления.
не является Гурвицевой, то возможен второй подход: алгоритм начинается с задания ВФЛ. Первый эффективно алгоритмизируется. При втором необходимо детально рассматривать особенности системы управления.
Пример 3. Случай нелинейной системыс 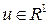 .
.
Введем систему с запаздыванием вида 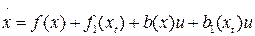 ,
, 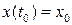 ,
, 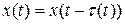 , (10)
, (10)
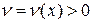 ,
, 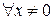 ,
, 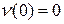 ,
, 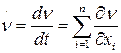 ;
;
По теореме Разумихина
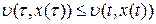 ,
, 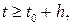
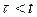 ,
,
Вычисляем производную в силу системы
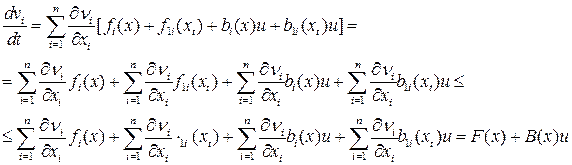
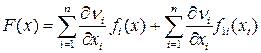 ,
, 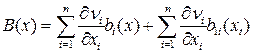
Рассмотрим множества 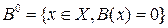 ,
, 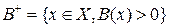 ,
, 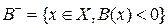 .
.
Теорема 2. Нечеткая система будет асимптотически устойчивой при выполнении следующих условий: 1) 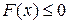 ,
, 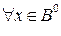 ; 2) при
; 2) при 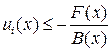 для
для 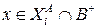 , при
, при 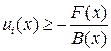 для
для 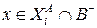 ; 3) множество
; 3) множество 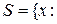 :
: 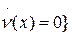 не будет содержать целых траекторий.
не будет содержать целых траекторий.
Доказательство, Полагаем . 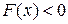 .
.
Случай 1. 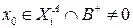 Тогда
Тогда 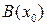 строго положительна.
строго положительна.
Из условия теоремы следует
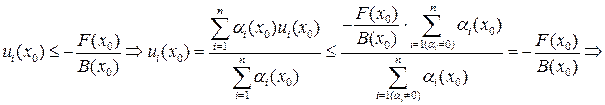
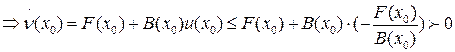
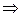
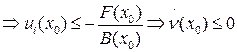
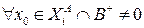
Случай 2. 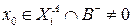
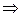
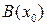 строго отрицательная.
строго отрицательная.
Из условия теоремы следует
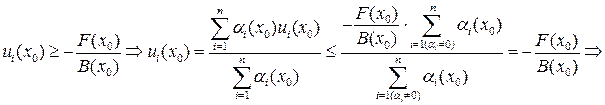
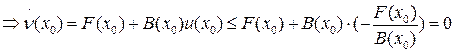
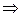
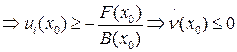
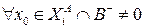
Случай 3. 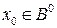 . Из условия теоремы
. Из условия теоремы 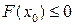
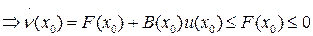
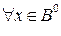
Из трех условий следует 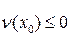
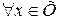 , откуда следует асимптотическая устойчивость.
, откуда следует асимптотическая устойчивость.
Если нет области 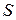 , то если
, то если 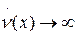
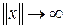 , тогда система будет асимптотически устойчивой в целом.
, тогда система будет асимптотически устойчивой в целом.
Задание.
1. Изучить создание системы управления общего вида, линейной системы, нелинейной системы.
2. Разработать собственную систему управления линейную и нелинейную.
Содержание отчета
1.Титульный лист; 2. Постановка задачи, исходные данные для задания (самостоятельно составить исходные данные для объекта); 3. Введение (краткое описание предметной области и задачи); 4. Разработанная собственная система управления линейная и нелинейная. Screenshots программной реализации в MATLAB; 5. Анализ качества переходных процессов. 6. Screenshots программной реализации в MATLAB. 3 Выводы по работе.
Практическое занятие №5
Нечеткое системное проектирование разработки нефтяных месторождений ( 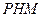 )
)
Цель работы:
- Идентификация нечетких целей функционирования системы 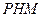
- Влияние факторов в формулировании нечетких целей 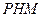 .
.
Теоретические сведения
В системном подходе к разработке нефтяных месторождений (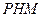 ) одним из основных является понятие цели. Под нечеткой целью
) одним из основных является понятие цели. Под нечеткой целью 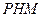 понимают будущий результат деятельности системы разработки (
понимают будущий результат деятельности системы разработки (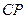 ), желательный для одного или нескольких участников разработки, который может быть достигнут за конечный срок
), желательный для одного или нескольких участников разработки, который может быть достигнут за конечный срок 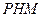 . Под нечеткой целью понимают цель
. Под нечеткой целью понимают цель  , которую можно описать как нечеткое множество в соответствующем пространстве параметров. Нечеткая цель, таким образом, тесно связана с общими характеристиками функционирования
, которую можно описать как нечеткое множество в соответствующем пространстве параметров. Нечеткая цель, таким образом, тесно связана с общими характеристиками функционирования 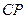 как сложной системы - неопределенностью, «размытостью» и неразличимостью. Основные заинтересованные участники
как сложной системы - неопределенностью, «размытостью» и неразличимостью. Основные заинтересованные участники  (компания, банк, потребитель, государство, местная власть) на стадии постановки задачи и целей
(компания, банк, потребитель, государство, местная власть) на стадии постановки задачи и целей  имеют дело с более «размытой» информацией о залежи, чем интегрированная команда специалистов на стадии проектирования. Так как на стадии составления технологического эксплуатационного объекта (
имеют дело с более «размытой» информацией о залежи, чем интегрированная команда специалистов на стадии проектирования. Так как на стадии составления технологического эксплуатационного объекта (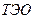 ), технологической схемы или проекта анализируется, сопоставляется информация о залежи, поступающая из различных источников, и формируется непротиворечивая, менее «размытая» информационная основа для проектирования. Средством достижения поставленных нечетких целей
), технологической схемы или проекта анализируется, сопоставляется информация о залежи, поступающая из различных источников, и формируется непротиворечивая, менее «размытая» информационная основа для проектирования. Средством достижения поставленных нечетких целей 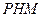 служат механизмы и способы функционирования сложной системы разработки нефтяных месторождение (
служат механизмы и способы функционирования сложной системы разработки нефтяных месторождение (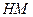 ). Рациональной
). Рациональной 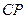 соответствует некоторая «размытая» область
соответствует некоторая «размытая» область 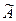 , в которой полностью достигаются поставленные нечеткие цели
, в которой полностью достигаются поставленные нечеткие цели 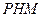 . Эта область полного достижения одной или нескольких целей
. Эта область полного достижения одной или нескольких целей 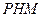 окружена областью частичного достижения одной или нескольких целей
окружена областью частичного достижения одной или нескольких целей 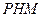 -
- 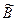 . Существует также область полного недостижения нечетких целей
. Существует также область полного недостижения нечетких целей 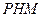 -
- 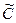 . Таким образом,
. Таким образом, 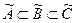 . Наиболее простой путь формализации таких областей - использование аппарата нечетких множеств.
. Наиболее простой путь формализации таких областей - использование аппарата нечетких множеств.
Идентификация нечетких целей функционирования системы РНМ Пример 1.На рисунке 5.1. представлены области для одной 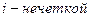
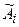 ,
, 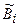 и
и 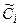 . Области
. Области 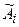 на оси абсцисс -
на оси абсцисс - 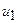 соответствует интервал
соответствует интервал 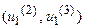 , а области
, а области 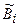 - интервал
- интервал 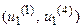 . Следовательно, с точки зрения теории нечетких множеств (
. Следовательно, с точки зрения теории нечетких множеств (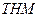 ) это можно интерпретировать следующим образом: степень принадлежности
) это можно интерпретировать следующим образом: степень принадлежности 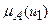 нечеткому множеству цели РНМ на отрезке
нечеткому множеству цели РНМ на отрезке 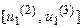 равна единице, а в интервалах
равна единице, а в интервалах 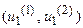 и
и 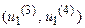 принимает значения от 0 до 1. Аналогично степень принадлежности по критерию
принимает значения от 0 до 1. Аналогично степень принадлежности по критерию 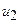 -
- 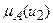 нечеткому множеству цели
нечеткому множеству цели  на отрезке
на отрезке 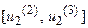 равна единице, а в интервалах
равна единице, а в интервалах 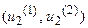 и
и 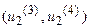 изменяется в пределах (0,1).
изменяется в пределах (0,1).
На рисунке 5.1. представлена также парето-оптимальная область размытых целей 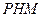 в пространстве критериев
в пространстве критериев 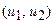 и построены функции принадлежности
и построены функции принадлежности 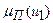 и
и 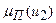 парето-оптимальному множеству нечеткой цели -
парето-оптимальному множеству нечеткой цели - 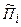 . При этом
. При этом 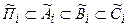 . Нечеткое множество всех целей
. Нечеткое множество всех целей 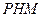 есть объединение множеств
есть объединение множеств 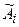 ,
, 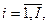 где
где 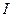 - количество целей:
- количество целей: 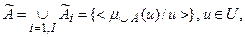 где
где 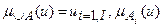 . Парето-оптимальное множество нечетких целей задается аналогично:
. Парето-оптимальное множество нечетких целей задается аналогично: 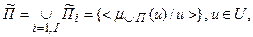 где
где 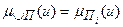 .
.
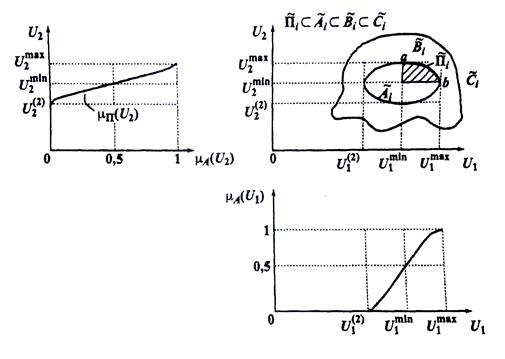
Рисунок 5.1. – Парето-оптимальная область размытой цели  в двухмерном критериальном пространстве параметров
в двухмерном критериальном пространстве параметров 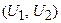 и соответствующие нечеткие функции принадлежности
и соответствующие нечеткие функции принадлежности 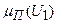 и
и 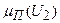 парето-оптимальному множеству нечеткой цели
парето-оптимальному множеству нечеткой цели 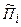 (дуга
(дуга  )
)
