Исследование автоматической системы управления (АСР) с аналоговым ПИ-регулятором и с fuzzy-регулятором
Цель работы:исследование автоматической системы управления (АСР) с аналоговым ПИ-регулятором и с fuzzy-регулятором
Теоретические сведения
Алгоритмы нечеткого вывода Мамдани (Mamdani)
Пусть заданы два нечетких правила:
П1: если х есть А1 и y есть В1, тогда z есть С1,
П2: если х есть А2 и y есть В2, тогда z есть С2.
1 Нечеткость. Находят степени принадлежности для предпосылок каждого правила: 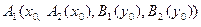 .
.
2 Нечеткий вывод. Определяют уровни «отсечения» для предпосылок каждого правила (операция min): 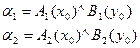 ,
,
определяют усеченные функции принадлежности 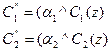
3 Композиция. Производится объединение найденных усеченных функций (операция max), получают нечеткое подмножество для переменной выхода с функцией принадлежности: 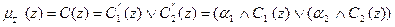
4 Дефаззификация. Приведение к четкости (определение z0), например, центроидным методом (как центр тяжести для кривой 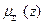 ):
): 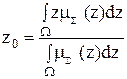 .
.
Алгоритм иллюстрируется на рисунке 3.1.
|
Пример 1.Открыть файл model2.mdlкаталога Demo из запущенного приложения Matlab. На экране должна быть изображена следующая структура АСР (рис. 3.2). Теперь при помощи инструментов графического интерфейса пользователя (GUI) пакета " 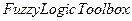 " создадим нечёткую систему, реализующую типовой аналоговый ПИ-регулятор. Заметим, что с помощью пакета "
" создадим нечёткую систему, реализующую типовой аналоговый ПИ-регулятор. Заметим, что с помощью пакета " 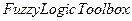 " можно строить нечеткие системы двух типов - Мамдани и Сугэно. Остановимся на системе типа Мамдани. Командой
" можно строить нечеткие системы двух типов - Мамдани и Сугэно. Остановимся на системе типа Мамдани. Командой  в окне MATLAB вызываем окно Редактора фази-инференционной системы (
в окне MATLAB вызываем окно Редактора фази-инференционной системы (  ), выбираем тип системы - Мамдани, задаём два входа - для пропорциональной и интегральной составляющих и называем входные переменные, например, x1 и x2, а выходную - y.
), выбираем тип системы - Мамдани, задаём два входа - для пропорциональной и интегральной составляющих и называем входные переменные, например, x1 и x2, а выходную - y.
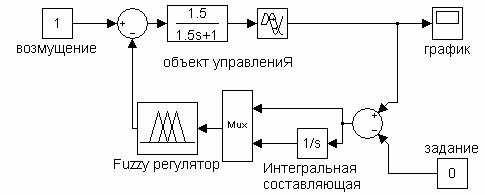
Рисунок 3.2 - Модель одноконтурной системы автоматического регулирования с ПИ-подобным fuzzy-регулятором
Из данного окна вызываем окно Редактора функций принадлежности (  ) двойным щелчком мыши по изображению переменной x1 или при помощи меню
) двойным щелчком мыши по изображению переменной x1 или при помощи меню  . Здесь для лингвистического описания каждой переменной выберем семь треугольных термов (NB,NM,NS,ZE,PS,PM,PB). Термы выходной переменной лучше выбирать непересекающимися. Это повысит чёткость регулирования. В этом же окне зададим диапазоны изменения переменных:
. Здесь для лингвистического описания каждой переменной выберем семь треугольных термов (NB,NM,NS,ZE,PS,PM,PB). Термы выходной переменной лучше выбирать непересекающимися. Это повысит чёткость регулирования. В этом же окне зададим диапазоны изменения переменных:
Для входных переменных регулятора рекомендуются симметричные диапазоны изменения, при этом
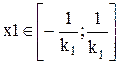 и
и 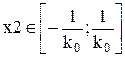 ,
,
где К1, К0 – оптимальные настройки пропорциональной и интегрирующей частей ПИ – регулятора в смысле какого-либо критерия.
Для выходной переменной регулятора диапазон изменения рекомендуется брать в виде 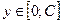 , где верхняя граница С при единичном ступенчатом воздействии варьируется от 1.1 до 2, чтобы выходной сигнал регулятора мог компенсировать это возмущение. По мере увеличения значения С уменьшается динамическая ошибка, но возрастают время регулирования и число колебаний переходного процесса. Поэтому рекомендуется С принимать равным 2, когда наблюдается оптимальное соотношение между величиной динамической ошибки, времени регулирования и количеством колебаний.
, где верхняя граница С при единичном ступенчатом воздействии варьируется от 1.1 до 2, чтобы выходной сигнал регулятора мог компенсировать это возмущение. По мере увеличения значения С уменьшается динамическая ошибка, но возрастают время регулирования и число колебаний переходного процесса. Поэтому рекомендуется С принимать равным 2, когда наблюдается оптимальное соотношение между величиной динамической ошибки, времени регулирования и количеством колебаний.
Теперь необходимо сформировать базу правил fuzzy-регулятора. В основу положен способ, предложенный в литературе.
Линейный непрерывный ПИ-регулятор с дифференциальным уравнением
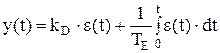
можно заменить близким по стратегии и логике управления fuzzy-регулятором, если в качестве его выходной переменной рассматривать приращение управляющего воздействия Δy. Тогда ПИ закон регулирования можно представить в следующей дифференциальной форме:
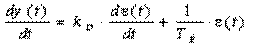 ,
,
или в разностной форме:
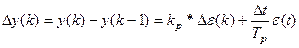 .
.
Таким образом, для входных переменных ε(k) и Δε(k) и выходной Δy(k) может быть синтезирован fuzzy-регулятор, реализующий нелинейный закон
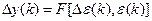 и эквивалентный в определённом смысле ПИ-регулятору.
и эквивалентный в определённом смысле ПИ-регулятору.
Для нашего случая x1 соответствует сигналу рассогласования ε(k), x2 соответствует приращению сигнала рассогласования Δε(k), а y соответствует Δy(k). Лингвистические правила для такого ПИ-подобного fuzzy-регулятора приведены в таблице 3.1.
Вызываем окно Редактора правил (Rule Editor) в меню Edit или нажатием Ctrl+3 и заполняем список правилами из таблицы 1.5. Правила формируются по типу: ЕСЛИ … И …, ТО…. Можно посмотреть пространство управления, вызвав окно Просмотра пространства управления(Surface Viewer) из меню View или комбинацией клавиш Ctrl+6. Полученный файл сохраним под именем fuzzy1.fis.
В окне параметров блока Fuzzy Logic Controller укажем имя файла fuzzy1. В окне модели в меню  выберем пункт
выберем пункт  . В открывшемся окне выберем вкладку
. В открывшемся окне выберем вкладку  и в поле
и в поле  напишем:
напишем:
fuzzy1=readfis('fuzzy1').
Данная команда будет каждый раз при открытии файла модели помещать файл fuzzy1.fis в WorkSpace (рабочее пространство системы MATLAB). Это необходимо для нормального функционирования модели. Стоит заметить, что при внесении изменений в fis-файл нужно помещать его исправленную версию в WorkSpace либо при помощи пункта Export/To Workspace меню File, либо комбинацией клавиш Ctrl+T, либо каждый раз закрытием и открытием файла модели.
Таблица 3.1 – Лингвистические правила для ПИ fuzzy-регулятора
| ε ∆ε | NB | NM | NS | ZE | PS | PM | PB |
| NB | NB | NB | NB | NB | NM | NS | ZE |
| NM | NB | NB | NB | NM | NS | ZE | PS |
| NS | NB | NB | NM | NS | ZE | PS | PM |
| ZE | NB | NM | NS | ZE | PS | PM | PB |
| PS | NM | NS | ZE | PS | PM | PB | PB |
| PM | NS | ZE | PS | PM | PB | PB | PB |
| PB | ZE | PS | PM | PB | PB | PB | PB |
В диалоговом окне 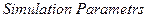 меню
меню 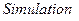 во вкладке
во вкладке 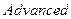 для опции
для опции 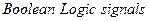 необходимо установить значение off. При этом блоки логики будут допускать переменные в форме с плавающей точкой.
необходимо установить значение off. При этом блоки логики будут допускать переменные в форме с плавающей точкой.
Запуск модели –  /
/  (Ctrl+T).
(Ctrl+T).
В папке Demo находится файл с правилами нечеткого вывода. Загрузка файла осуществляется из окна редактора правил Rule Viewer: во вкладке File/Import From Disk открыть файл fuzzy1.fsi. Затем нужно поместить правила в WorkSpace системы (описано выше).
Пример 2.Работу разработанного fuzzy-регулятора необходимо сравнить с аналоговой системой регулирования (рис. 3.3).
Дифференциальное уравнение ПИД-регулятора имеет вид:
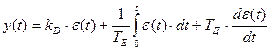 .
.
Для исследования ПИ-регулятора в блоке настроек регулятора необходимо в поле параметра ТД (настройка дифференцирующей части ПИД-регулятора) установить значение 0.
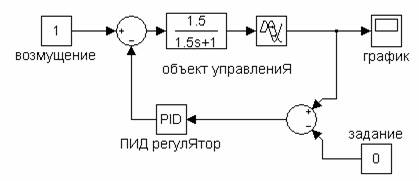
Рисунок 3.3 - Модель одноконтурной системы автоматического регулирования
Задание.Исследовать АСР с аналоговым ПИ-регулятором и fuzzy-регулятором. В качестве модели объекта принять апериодическое звено, параметры объекта принять из таблицы 3.2.
Таблица 1.7 – Параметры объекта к заданию 2
| Вариант | ||||||||||
| K | 1.5 | 1.8 | 1.3 | 1.9 | 2.2 | 1.4 | 2.5 | 2.3 | 2.4 | |
| T | 1.8 | 1.8 | 1.5 | 1.5 | 1.3 | 1.5 | 1.5 | 1.6 | 1.4 | 1.7 |
Настройки ПИ-регулятора определить по формульному методу:
| Регулятор | Апериодический процесс | Процесс с перерегулированием 20 % | Процесс с минимальным временем регулирования |
| ПИ | 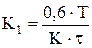 , , 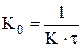 | 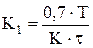 , , 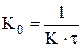 | 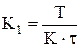 , , 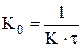 |
Порядок выполнения работы
1. Ознакомиться с краткими теоретическими сведениями и примерами.
2. Выполнить задание.
3. Подготовить отчет о работе с краткими теоретическими сведениями.
4. Исходные данные для задачи. Блок схема моделируемой системы, графики переходных процессов для аналогового и нечеткого регуляторов. Параметры элементов системы нечеткого вывода проектируемой системы (тип функций принадлежности, способ реализации логических выражений, способ дефаззификации). Анализ качества переходных процессов.
5. Правила нечеткого вывода, форма функций принадлежности на всем диапазоне значений аргумента, результат вывода в графическом виде, относительная погрешность аппроксимации. Результат оформить в форме таблицы:
| X | ||||
| Y | ||||
| yаппрокс. | ||||
| σ, % |
4 Выводы по работе.
Практическое занятие №4

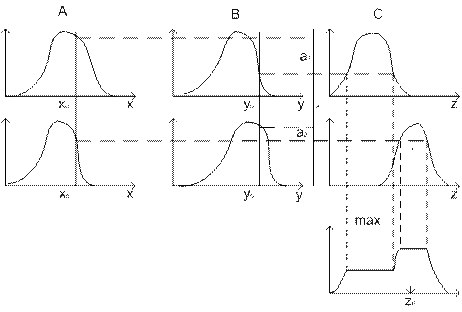 Рисунок 3.1 – Графическая интерпретация алгоритма Мамдани
Рисунок 3.1 – Графическая интерпретация алгоритма Мамдани