Искусственные нейронные сети и нечеткая логика в задачах контроля и управления
К.Л. Горшкова
Искусственные нейронные сети и нечеткая логика в задачах контроля и управления
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по проведению практических занятий и организации самостоятельной работы
по дисциплине «Искусственные нейронные сети и нечеткая логика в задачах контроля и управления»
для магистров направления подготовки
15.04.04 «Автоматизация технологических процессов и производств»
очной формы обучения
г.Альметьевск, 2016г.
УДК 519.87
Г-67
Горшкова К.Л.
Г-67 Искусственные нейронные сети и нечеткая логика в задачах контроля и управления: Методические указания по проведению практических занятий и организации самостоятельной работы по дисциплине «Искусственные нейронные сети и нечеткая логика в задачах контроля и управления» для магистров направления подготовки 15.04.04 «Автоматизация технологических процессов и производств» очной формы обучения. – Альметьевск: Альметьевский государственный нефтяной институт, 2016. – 64с.
Методические указания содержат краткие сведения из теории и практические материалы, целью выполнения которых является разработка пакета прикладных программ для комплексной оценки состояния сложных систем на основе использования инструментария универсальных математических систем MatLab, примеры и задания по вариантам.
Печатается по решению Учебно-методического Совета АГНИ.
Рецензент:
Томус Ю.Б. - к.т.н., доцент.
©Альметьевский государственный
нефтяной институт, 2016
СОДЕРЖАНИЕ
| Введение……………………………………………………………………………………….. | |
| Практическое занятие №1. Изучение основных операций над нечеткими множествами…………………………………………………………………………………. | |
| Практическое занятие №2. Построение нечеткой аппроксимирующей функции у=х2… | |
| Практическое занятие №3. Исследование автоматической системы управления (АСР) с аналоговым ПИ-регулятором и fuzzy-регулятором……………………………………… | |
| Практическое занятие №4. Синтез нечетких алгоритмов управления на основе метода векторных функций Ляпунова……………………………………………………………… | |
| Системы управления общего вида………………………………………………………….. | |
| Линейные системы……………………………………………………………………………. | |
| Случай нелинейной системы………………………………………………………………… | |
| Практическое занятие №5. Нечеткое системное проектирование разработки нефтяных месторождений (РНМ)……………………………………………………………………….. | |
| Идентификация нечетких целей функционирования системы РНМ……………………. | |
| Влияние факторов в формулировании нечетких целей РНМ……………………………. | |
| Практическое занятие №6. Математическая процедура выделение эксплуатационных объектов (ВЭО)………………………………………………………………………………. | |
| Приближенное описание параметров с помощью лингвистических переменных……… | |
| Формирование системы правил ВЭО………………………………………………………. | |
| Построение функций принадлежности параметров нечеткому множеству «эксплуатационный объект»………………………………………………………………… | |
| Построение диаграммы нечетких, «размытых отношений»……………………………… | |
| Практическое занятие №7. Линейные сети……………………………………………… | |
| Разработка структурной схемы линейной нейронной сети………………………………. | |
| Разработка алгоритма создания и моделирования линейной нейронной сети………….. | |
| Определение параметров созданной нейронной сети……………………………………. | |
| Практическое занятие №8. Обучение и настройка линейной сети…………………….. | |
| Процедура настройки посредством прямого расчета……………………………………… | |
| Построение графиков для получения значений веса и смещения, поверхности функции ошибки…………………………………………………………………………………………… | |
| Практическое занятие №9. Обучение линейной сети……………………………………. | |
| Обучающее правило наименьших квадратов…………………………………………………. | |
| Процедура обучения……………………………………………………………………………. | |
| Построений линий уровня и траектории обучения………………………………………… | |
| Практическое занятие №10. Применение линейных сетей……………………………… | |
| Задача классификации векторов……………………………………………………………… | |
| Построение персептронной нейронной сети для задач классификации разделимых векторов…………………………………………………………………………………………. | |
| Практическое занятие №11. Применение линейных сетей……………………………….. | |
| Проверка правильности решения задачи фильтрации сигнала сетью…………………….. | |
| Адаптируемые линейные сети………………………………………………………………… | |
| Практическое занятие №12. Работа в программных приложениях пакета Matlab…….. | |
| Задачи с начальными условиями (Исследование потока нефти на входе насоса при его отключения)……………………………………………………………………………………. | |
| Задача с граничными условиями (ЗГУ)……………………………………………………… | |
| Самостоятельная работа…………………………………………………………………….. | |
| Список использованной литературы……………………………………………………….. | |
| Приложение А |
Введение
Цель данного методического указания – обеспечить обучаемым комплекс ориентирующих знаний по основным понятиям интеллектуальных систем и возможностям их использования в различных предметных областях.
Методическое указание составлено на основе анализа литературы, систематизации и частичной переработки материалов источников [1…30], интернет - источников и прочих материалов и является учебно-методическим трудом, отражающее видение автора на структуру и наполнение дисциплины «Искусственные нейронные сети и нечеткая логика в задачах контроля и управления» в соответствии ФГОС ВО по направлению 15.04.04 «Автоматизация технологических процессов и производств» и разработанной рабочей программы дисциплины [7].
Изучаются математические и алгоритмические основы интеллектуальных систем в задачах контроля и управления: модели представления знаний на основе систем продукций, выводы на знаниях; нечеткая информация и выводы; нейронные сети; методы эвристического поиска решений и программирования задач.
Практическое занятие № 1
Теоретические сведения
Значительный шаг в направлении развития теории нечетких множеств (ТНМ) сделал профессор Калифорнийского университета Лотфи А. Заде (1965 г. - публикация работы “ 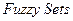 ”). Заде расширил понятие множества, допустил, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0, 1]. Такие множества были названы им нечеткими (
”). Заде расширил понятие множества, допустил, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0, 1]. Такие множества были названы им нечеткими ( 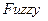 ).
).
Пусть Е – универсальное множество, х – элемент Е, Р – некоторое свойство. Обычное (четкое) множество А универсального множества Е, элементы которого удовлетворяют свойству Р, определяются как множество упорядоченных пар 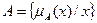 , где
, где 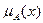 - характеристическая функция, принимающая значение 1, если х удовлетворяет свойству Р, и 0 – в противном случае.
- характеристическая функция, принимающая значение 1, если х удовлетворяет свойству Р, и 0 – в противном случае.
В ТНМ для элементов х из Е нет однозначного ответа «да/нет» относительно свойства Р. В связи с этим нечеткое множество А универсального множества Е определяется как множество упорядоченных пар с функцией принадлежности 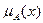 , принимающей значение в некотором упорядоченном множестве М (например, М=[0, 1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М={0, 1},то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
, принимающей значение в некотором упорядоченном множестве М (например, М=[0, 1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М={0, 1},то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
Основные операции над нечеткими множествами:
Включение.Пусть А и В нечеткие множества на универсальном множестве Е. А содержится в В, если 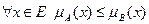 . Обозначается А
. Обозначается А 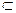 В.
В.
Равенство.А и В равны, если 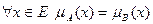 . Обозначение: А=В.
. Обозначение: А=В.
Дополнение.Пусть М=[0,1], А и В дополняют друг друга, если 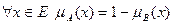 . Обозначается В=
. Обозначается В= 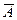 или
или 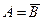 .
.
Пересечение. 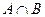 - наименьшее нечеткое подмножество, содержащееся одновременно в А и В:
- наименьшее нечеткое подмножество, содержащееся одновременно в А и В: 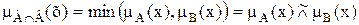 .
.
Или, по другому, определение в классе треугольных норм (t – норма).
Типичными t - нормами являются [2, 3]:
- операция min как нечеткое логическое произведение с нечеткими переменными Х1, Х2: 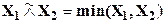 ;
;
- алгебраическое произведение 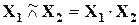 .
.
Объединение. 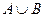 - наибольшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:
- наибольшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:
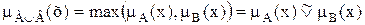 .
.
Или, по другому, определение в классе треугольных конорм (s – норма).
Типичными s - нормами являются:
- операция нечеткого логического сложения 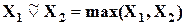 ;
;
- алгебраическая сумма 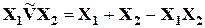 ,
,
где «~» означает нечеткую логическую операцию.
Разность.А-В= 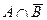 с функцией принадлежности:
с функцией принадлежности: 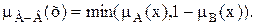
Нечеткие отношения.Нечеткое n-мерное отношение определяется как нечеткое подмножество R на Е, принимающее свои значения в М. В случае n=2 и М=[0,1] нечетким отношением R между множествами Х=Е1 и Y=Е2 будет называться функция R: (X, Y) → [0,1], которая ставит в соответствие каждой паре элементов (x,y) 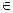 X x Y величину
X x Y величину 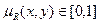 .
.
Обозначение: 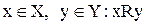 .
.
Алгебраические операции над нечеткими отношениями аналогичны операциям с нечетким множествам.
Композиция (свертка) двух нечетких отношений.Пусть R1 – нечеткое отношение R1: (X x Y) →[0,1] между X и Y, и R2 – нечеткое отношение R2: (Y x Z) →[0,1] между Y и Z. Нечеткое отношение между X и Z обозначается R1●R2 и определяется как
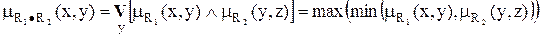 , где символ
, где символ 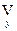 - обозначает операцию выбора наибольшего по y значения и называется (max-min)-сверткой отношений R1 и R2.
- обозначает операцию выбора наибольшего по y значения и называется (max-min)-сверткой отношений R1 и R2.
Пример 1.
1Пусть Е ={x1, x2, x3, x4, x5}; А – нечеткое множество, для которого 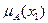 =0,3;
=0,3; 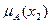 =0;
=0; 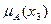 =1;
=1; 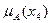 =0,6;
=0,6; 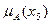 =0,9.
=0,9.
Тогда А можно представить в виде
А = {0,3/x1; 0/x2; 1/x3; 0,6/x4; 0,9/x5}.
Пример 2.
Пусть заданы отношения R1 и R2.
Таблица 1.1
| R1 | y1 | y2 | y3 |
| x1 | 0,1 | 0,7 | 0,4 |
| x2 | 0,5 |
Таблица 1.2
| R2 | z1 | z2 | z3 | z4 |
| y1 | 0,9 | 0,2 | ||
| y2 | 0,3 | 0,6 | 0,9 | |
| y3 | 0,1 | 0,5 |
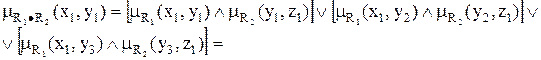
= (0,1 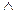 0,9)
0,9) 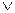 (0,7
(0,7 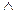 0,3)
0,3) 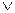 (0,4
(0,4 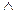 0,1)=0,1
0,1)=0,1 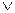 0,3
0,3 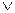 0,1=0,3.
0,1=0,3.
Таблица 1.3
| R1· R2 | z1 | z2 | z3 | z4 |
| х1 | 0,3 | 0,6 | 0,1 | |
| х2 | 0,9 | 0,5 |
Пример 3. Пусть на универсальном множестве E заданы нечеткие множества A, B, C:
A= {1/x1; 0/x2; 0/x3; 0.1/x4},
B= {1/x1; 0/x2; 0.1/x3; 0.2/x4},
C= {1/x1; 0.2/x2; 0.1/x3; 0.8/x4}.
Определим, выполняются ли условия:
1) 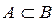 – включение. Данное условие выполняется, т.е. А содержится в B, так как
– включение. Данное условие выполняется, т.е. А содержится в B, так как 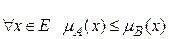 .
.
2) 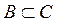 – включение. Данное условие выполняется, т.е. А содержится в B, так как
– включение. Данное условие выполняется, т.е. А содержится в B, так как 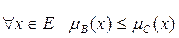 .
.
3) 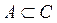 – включение. Данное условие выполняется, т.е. А содержится в B, так как
– включение. Данное условие выполняется, т.е. А содержится в B, так как 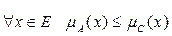 .
.
4) 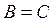 – равенство. Данное условие не выполняется, так как не выполняется условие
– равенство. Данное условие не выполняется, так как не выполняется условие 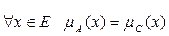 .
.
5) 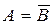 – дополнение. А и B дополняют друг друга, если
– дополнение. А и B дополняют друг друга, если 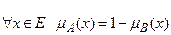 . Следовательно, данное условие не выполняется.
. Следовательно, данное условие не выполняется.
6) 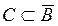 – дополнение. А и B дополняют друг друга, если
– дополнение. А и B дополняют друг друга, если 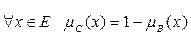 . Следовательно, данное условие не выполняется.
. Следовательно, данное условие не выполняется.
7) 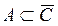 – дополнение. А и B дополняют друг друга, если
– дополнение. А и B дополняют друг друга, если 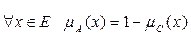 . Следовательно, данное условие не выполняется.
. Следовательно, данное условие не выполняется.
Рассчитаем:
1) 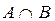 – пересечение, т.е. наибольшее нечеткое подмножество, содержащее одновременно A и B, функция принадлежности для которого рассчитывается по формуле:
– пересечение, т.е. наибольшее нечеткое подмножество, содержащее одновременно A и B, функция принадлежности для которого рассчитывается по формуле: 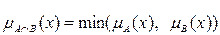 .
.
Тогда получаем 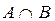 ={1/x1; 0/x2; 0/x3; 0.1/x4}.
={1/x1; 0/x2; 0/x3; 0.1/x4}.
2) 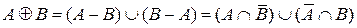 с функцией принадлежности:
с функцией принадлежности: 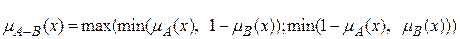 .
.
Тогда получаем 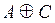 ={0/x1; 0/x2; 0.1/x3; 0.1/x4}.
={0/x1; 0/x2; 0.1/x3; 0.1/x4}.
3) 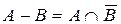 с функцией принадлежности:
с функцией принадлежности:
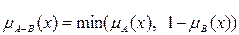 .
.
Тогда получаем  ={0/x1; 0/x2; 0/x3; 0.1/x4}.
={0/x1; 0/x2; 0/x3; 0.1/x4}.
4) 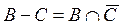 с функцией принадлежности:
с функцией принадлежности:
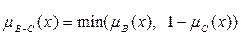 .
.
Тогда получаем 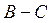 ={0/x1; 0/x2; 0.1/x3; 0.2/x4}.
={0/x1; 0/x2; 0.1/x3; 0.2/x4}.
Заданияпредставлены в приложении 1 для решения основных операций над множествами.
Порядок выполнения работы
1. Ознакомиться с краткими теоретическими сведениями и примерами.
2. Для решения основных операций над множествами решить задания представленные в приложение 1.
3. Подготовить отчет о работе с краткими теоретическими сведениями и примерами и с представлением и объяснением полученных результатов.
Практическое занятие № 2
Построение нечеткой аппроксимирующей функции у=х2
Цель работы:изучить создание системы нечеткого вывода для аппроксимации функции.
Теоретические сведения
В экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:
П1: если х есть А1, то y есть В1,
П2: если х есть А2,то y есть В2,
…
Пn: если х есть Аn,то y есть Вn,
где х – входная переменная, y – переменная вывода, А и В – функции принадлежности, определенные на х и y соответственно.
Знания эксперта А→В отражает нечеткое причинное отношение предпосылки и заключения, поэтому его называют нечетким отношением:
R= А→В, где «→» - нечеткая импликация.
Отношение R можно рассматривать как нечеткое подмножество прямого произведения Х ´ Y полного множества предпосылок X и заключений Y. Таким образом, процесс получения (нечеткого) результата вывода В′ с использованием данного наблюдения А′ и значения А→В можно представить в виде В′= А′● R= А′●( А→В).
Алгоритм нечеткого вывода:
1 Нечеткость (фаззификация, fuzzification). Функции принадлежности, определенные для входных переменных, применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила).
2 Логический вывод. Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила. Это приводит к одному нечеткому подмножеству, которое будет назначено переменной вывода для каждого правила. В качестве правил логического вывода используются только операции min (минимума) или prod (умножение).
3 Композиция. Нечеткие подмножества, назначенные для каждой переменной вывода (во всех правилах), объединяются вместе, чтобы сформировать одно нечеткое подмножество для каждой переменной вывода. При подобном объединении обычно используются операции max (максимум) или sum (сумма).
4 Дефаззификация – приведение к четкости (defuzzification). Преобразование нечеткого набора выводов в число.
Алгоритмы нечеткого вывода Сугено ( 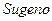 ) и Такаги (
) и Такаги ( 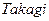 )
)
Сугено ( 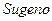 ) и Такаги (
) и Такаги ( 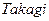 ) использовали набор правил в следующей форме:
) использовали набор правил в следующей форме:
П1: если х есть А1 и y есть В1, тогда z=a1x+b1y,
П2: если х есть А2 и y есть В2, тогда z =a2x+b2y.
1 Первый этап – аналогично алгоритму Мамдани.
2 Определение 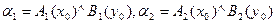 и индивидуальные выходы правил:
и индивидуальные выходы правил: 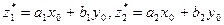 .
.
3 Определяется значение переменной вывода: 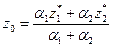 .
.
Представленная форма правил иллюстрирует алгоритм Сугено 1-го порядка. Если правила записаны в форме:
П1: если х есть А1 и y есть В1, тогда z=с1,
П2: если х есть А2 и y есть В2, тогда z =с2,
то задан алгоритм Сугено 0-го порядка.
Иллюстрация алгоритма Сугено 0-го порядка представлена на рисунке 1.1.
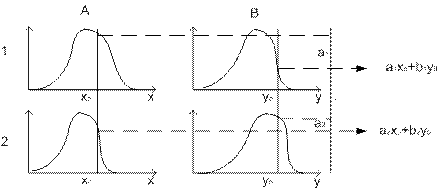
|
Пример.Построение нечеткой аппроксимирующей функции у=х2.
Исходные данные для аппроксимации представлены в таблице 2.1.
Таблица 2.1
Значения x и y
| X | -1 | -0,6 | 0,4 | ||
| Y | 0,36 | 0,16 |
1 Командой 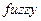 , из режима командной строки запускается основная интерфейсная программа пакета
, из режима командной строки запускается основная интерфейсная программа пакета 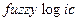 – редактор нечеткой системы вывода.
– редактор нечеткой системы вывода.
2 В меню 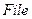 выбрать команду
выбрать команду 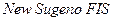 .
.
3 Выбрать входной элемент системы input1 и ввести в поле  обозначение входной переменной (х).
обозначение входной переменной (х).
4 Войти в режим редактирования функции принадлежности –  (двойное нажатие левой клавиши мыши). Выбором
(двойное нажатие левой клавиши мыши). Выбором  (добавить функцию принадлежности) задать тип функции принадлежности (
(добавить функцию принадлежности) задать тип функции принадлежности ( 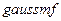 ) и количество (5).
) и количество (5).
5 Установить диапазон ( 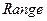 ) изменения х от -1 до 1 (определяется заданным диапазоном х).
) изменения х от -1 до 1 (определяется заданным диапазоном х).
6 Совместить ординаты максимумов функций принадлежности с значениями аргумента x.
Шаг выполняется двумя способами: выделить редактируемую функцию принадлежности, перетащить мышью кривую функции принадлежности; более точную установку проводят заданием числовых значений параметров функции принадлежности в поле 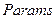 (первое значение определяет размах кривой, второе – положение центра).
(первое значение определяет размах кривой, второе – положение центра).
В поле 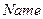 вводится имя функции принадлежности (1- bn, 2 – n, 3 (центральная) – z, 4 – p, 5 – bp).
вводится имя функции принадлежности (1- bn, 2 – n, 3 (центральная) – z, 4 – p, 5 – bp).
Выйти из редактора функций принадлежности – 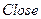 .
.
7 Ввести в поле название выходной переменной 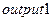 = (y), войти в режим редактирования функций принадлежности.
= (y), войти в режим редактирования функций принадлежности.
8 Задать вид функции принадлежности для выходной переменной. Предлагается выбрать в качестве функции принадлежности линейные (linear) или постоянные ( 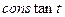 ) – в зависимости от алгоритма Сугено (1-го или 0-го порядка). В поставленной задаче необходимо выбрать постоянные функции принадлежности с общим числом 4 (по числу различающихся значений y). Нажать Ok.
) – в зависимости от алгоритма Сугено (1-го или 0-го порядка). В поставленной задаче необходимо выбрать постоянные функции принадлежности с общим числом 4 (по числу различающихся значений y). Нажать Ok.
9 Установить диапазон ( 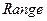 ) – [0, 1]. Изменить значения (
) – [0, 1]. Изменить значения ( 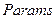 ) и задать для выходных переменных имена (
) и задать для выходных переменных имена (  ) соответственно 0; 0,16; 0,36; 1. Закрыть редактор.
) соответственно 0; 0,16; 0,36; 1. Закрыть редактор.
10 Перейти в редактор привил (  ) (дважды щелкнуть на средний белый квадрат разрабатываемой структуры системы нечеткого вывода). При вводе каждого правила необходимо обозначить соответствие между каждой функцией принадлежности аргумента x и числовым значением y. Кривая, обозначенная bn, соответствует y=1, для чего выбирается в левом поле (с заголовком x is) вариант bn, а в правом – 1 и нажимается кнопка
) (дважды щелкнуть на средний белый квадрат разрабатываемой структуры системы нечеткого вывода). При вводе каждого правила необходимо обозначить соответствие между каждой функцией принадлежности аргумента x и числовым значением y. Кривая, обозначенная bn, соответствует y=1, для чего выбирается в левом поле (с заголовком x is) вариант bn, а в правом – 1 и нажимается кнопка  . Введенное правило появится в окне правил в виде
. Введенное правило появится в окне правил в виде 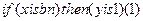 .
.
Аналогично вводятся все правила (всего 5). Закрыть окно редактора правил и вернуться в окно FIS-редактора. Построение системы закончено.
Сохранить на диске (  ) созданную систему. Перейти в редактор функций принадлежности (
) созданную систему. Перейти в редактор функций принадлежности (  ). Из окна редактора командой можно перейти в окно просмотра правил (
). Из окна редактора командой можно перейти в окно просмотра правил (  ), просмотра поверхности (
), просмотра поверхности (  ).
).
В окне просмотра правил иллюстрируется процесс принятия решения (вычисления y). Красная вертикальная черта, пересекающая графики в правой части окна, которую можно перемещать с помощью мыши, позволяет изменять значения переменной входа (либо вводят значение с клавиатуры в поле Input), при этом соответственно изменяется значение выхода.
Просмотр кривой y(x) осуществляется командой 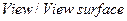 . Большая погрешность аппроксимации заданной зависимости объясняется малым числом экспериментов.
. Большая погрешность аппроксимации заданной зависимости объясняется малым числом экспериментов.
С помощью рассмотренных редакторов на любом этапе проектирования нечеткой модели можно внести необходимые коррективы, например задание пользовательской функции принадлежности.
В рассмотренном примере использованы следующие операции, устанавливаемые по умолчанию в алгоритме Сугено:
- логический вывод организуется с помощью операции логического умножения (prod);
- композиция организуется с помощью операции логической суммы (вероятностного ИЛИ, probor);
- приведение к четкости (дефаззификация) организуется дискретным вариантом центроидного метода (взвешенным средним, wtaver).
Задание.Создать систему нечеткого вывода для аппроксимации функции y=k*x2 (вариант см. в таблице 2.2). Для аппроксимации взять 10 значений функции.
Таблица 2.2 – Варианты задания для аппроксимации функции
| Вариант | ||||||||||
| k | 1.5 | 1.8 | 1.3 | 1.9 | 2.2 | 1.4 | 2.5 | 2.3 | 2.4 | |
| mf input | trimf | gaussmf | trimf | gaussmf | trimf | trimf | trimf | gaussmf2 | trimf | gaussmf |
Порядок выполнения работы
1. Ознакомиться с краткими теоретическими сведениями и примерами.
2. Согласно варианту задания для аппроксимации функции создать систему нечеткого вывода.
3. Подготовить отчет о работе с краткими теоретическими сведениями и примерами, с представлением и объяснением полученных результатов, графиков, вывод.
Практическое занятие № 3
Теоретические сведения
Алгоритмы нечеткого вывода Мамдани (Mamdani)
Пусть заданы два нечетких правила:
П1: если х есть А1 и y есть В1, тогда z есть С1,
П2: если х есть А2 и y есть В2, тогда z есть С2.
1 Нечеткость. Находят степени принадлежности для предпосылок каждого правила: 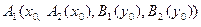 .
.
2 Нечеткий вывод. Определяют уровни «отсечения» для предпосылок каждого правила (операция min): 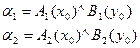 ,
,
определяют усеченные функции принадлежности 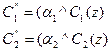
3 Композиция. Производится объединение найденных усеченных функций (операция max), получают нечеткое подмножество для переменной выхода с функцией принадлежности: 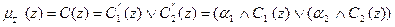
4 Дефаззификация. Приведение к четкости (определение z0), например, центроидным методом (как центр тяжести для кривой 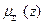 ):
): 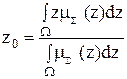 .
.
Алгоритм иллюстрируется на рисунке 3.1.
|
Пример 1.Открыть файл model2.mdlкаталога Demo из запущенного приложения Matlab. На экране должна быть изображена следующая структура АСР (рис. 3.2). Теперь при помощи инструментов графического интерфейса пользователя (GUI) пакета " 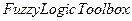 " создадим нечёткую систему, реализующую типовой аналоговый ПИ-регулятор. Заметим, что с помощью пакета "
" создадим нечёткую систему, реализующую типовой аналоговый ПИ-регулятор. Заметим, что с помощью пакета "  " можно строить нечеткие системы двух типов - Мамдани и Сугэно. Остановимся на системе типа Мамдани. Командой
" можно строить нечеткие системы двух типов - Мамдани и Сугэно. Остановимся на системе типа Мамдани. Командой 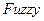 в окне MATLAB вызываем окно Редактора фази-инференционной системы (
в окне MATLAB вызываем окно Редактора фази-инференционной системы (  ), выбираем тип системы - Мамдани, задаём два входа - для пропорциональной и интегральной составляющих и называем входные переменные, например, x1 и x2, а выходную - y.
), выбираем тип системы - Мамдани, задаём два входа - для пропорциональной и интегральной составляющих и называем входные переменные, например, x1 и x2, а выходную - y.
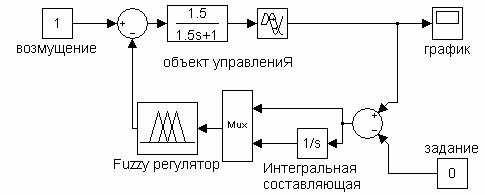
Рисунок 3.2 - Модель одноконтурной системы автоматического регулирования с ПИ-подобным fuzzy-регулятором
Из данного окна вызываем окно Редактора функций принадлежности (  ) двойным щелчком мыши по изображению переменной x1 или при помощи меню
) двойным щелчком мыши по изображению переменной x1 или при помощи меню  . Здесь для лингвистического описания каждой переменной выберем семь треугольных термов (NB,NM,NS,ZE,PS,PM,PB). Термы выходной переменной лучше выбирать непересекающимися. Это повысит чёткость регулирования. В этом же окне зададим диапазоны изменения переменных:
. Здесь для лингвистического описания каждой переменной выберем семь треугольных термов (NB,NM,NS,ZE,PS,PM,PB). Термы выходной переменной лучше выбирать непересекающимися. Это повысит чёткость регулирования. В этом же окне зададим диапазоны изменения переменных:
Для входных переменных регулятора рекомендуются симметричные диапазоны изменения, при этом
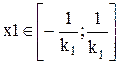 и
и 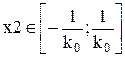 ,
,
где К1, К0 – оптимальные настройки пропорциональной и интегрирующей частей ПИ – регулятора в смысле какого-либо критерия.
Для выходной переменной регулятора диапазон изменения рекомендуется брать в виде 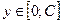 , где верхняя граница С при единичном ступенчатом воздействии варьируется от 1.1 до 2, чтобы выходной сигнал регулятора мог компенсировать это возмущение. По мере увеличения значения С уменьшается динамическая ошибка, но возрастают время регулирования и число колебаний переходного процесса. Поэтому рекомендуется С принимать равным 2, когда наблюдается оптимальное соотношение между величиной динамической ошибки, времени регулирования и количеством колебаний.
, где верхняя граница С при единичном ступенчатом воздействии варьируется от 1.1 до 2, чтобы выходной сигнал регулятора мог компенсировать это возмущение. По мере увеличения значения С уменьшается динамическая ошибка, но возрастают время регулирования и число колебаний переходного процесса. Поэтому рекомендуется С принимать равным 2, когда наблюдается оптимальное соотношение между величиной динамической ошибки, времени регулирования и количеством колебаний.
Теперь необходимо сформировать базу правил fuzzy-регулятора. В основу положен способ, предложенный в литературе.
Линейный непрерывный ПИ-регулятор с дифференциальным уравнением
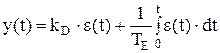
можно заменить близким по стратегии и логике управления fuzzy-регулятором, если в качестве его выходной переменной рассматривать приращение управляющего воздействия Δy. Тогда ПИ закон регулирования можно представить в следующей дифференциальной форме:
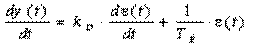 ,
,
или в разностной форме:
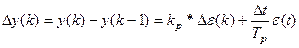 .
.
Таким образом, для входных переменных ε(k) и Δε(k) и выходной Δy(k) может быть синтезирован fuzzy-регулятор, реализующий нелинейный закон
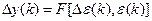 и эквивалентный в определённом смысле ПИ-регулятору.
и эквивалентный в определённом смысле ПИ-регулятору.
Для нашего случая x1 соответствует сигналу рассогласования ε(k), x2 соответствует приращению сигнала рассогласования Δε(k), а y соответствует Δy(k). Лингвистические правила для такого ПИ-подобного fuzzy-регулятора приведены в таблице 3.1.
Вызываем окно Редактора правил (Rule Editor) в меню Edit или нажатием Ctrl+3 и заполняем список правилами из таблицы 1.5. Правила формируются по типу: ЕСЛИ … И …, ТО…. Можно посмотреть пространство управления, вызвав окно Просмотра пространства управления(Surface Viewer) из меню View или комбинацией клавиш Ctrl+6. Полученный файл сохраним под именем fuzzy1.fis.
В окне параметров блока Fuzzy Logic Controller укажем имя файла fuzzy1. В окне модели в меню  выберем пункт
выберем пункт  . В открывшемся окне выберем вкладку
. В открывшемся окне выберем вкладку  и в поле
и в поле 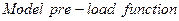 напишем:
напишем:
fuzzy1=readfis('fuzzy1').
Данная команда будет каждый раз при открытии файла модели помещать файл fuzzy1.fis в WorkSpace (рабочее пространство системы MATLAB). Это необходимо для нормального функционирования модели. Стоит заметить, что при внесении изменений в fis-файл нужно помещать его исправленную версию в WorkSpace либо при помощи пункта Export/To Workspace меню File, либо комбинацией клавиш Ctrl+T, либо каждый раз закрытием и открытием файла модели.
Таблица 3.1 – Лингвистические правила для ПИ fuzzy-регулятора
| ε ∆ε | NB | NM | NS | ZE | PS | PM | PB |
| NB | NB | NB | NB | NB | NM | NS | ZE |
| NM | NB | NB | NB | NM | NS | ZE | PS |
| NS | NB | NB | NM | NS | ZE | PS | PM |
| ZE | NB | NM | NS | ZE | PS | PM | PB |
| PS | NM | NS | ZE | PS | PM | PB | PB |
| PM | NS | ZE | PS | PM | PB | PB | PB |
| PB | ZE | PS | PM | PB | PB | PB | PB |
В диалоговом окне 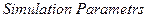 меню
меню 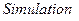 во вкладке
во вкладке 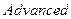 для опции
для опции 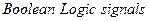 необходимо установить значение off. При этом блоки логики будут допускать переменные в форме с плавающей точкой.
необходимо установить значение off. При этом блоки логики будут допускать переменные в форме с плавающей точкой.
Запуск модели –  /
/  (Ctrl+T).
(Ctrl+T).
В папке Demo находится файл с правилами нечеткого вывода. Загрузка файла осуществляется из окна редактора правил Rule Viewer: во вкладке File/Import From Disk открыть файл fuzzy1.fsi. Затем нужно поместить правила в WorkSpace системы (описано выше).
Пример 2.Работу разработанного fuzzy-регулятора необходимо сравнить с аналоговой системой регулирования (рис. 3.3).
Дифференциальное уравнение ПИД-регулятора имеет вид:
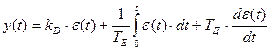 .
.
Для исследования ПИ-регулятора в блоке настроек регулятора необходимо в поле параметра ТД (настройка дифференцирующей части ПИД-регулятора) установить значение 0.
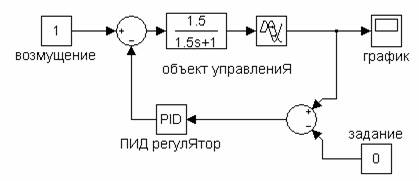
Рисунок 3.3 - Модель одноконтурной системы автоматического регулирования
Задание.Исследовать АСР с аналоговым ПИ-регулятором и fuzzy-регулятором. В качестве модели объекта принять апериодическое звено, параметры объекта принять из таблицы 3.2.
Таблица 1.7 – Параметры объекта к заданию 2
| Вариант | ||||||||||
| K | 1.5 | 1.8 | 1.3 | 1.9 | 2.2 | 1.4 | 2.5 | 2.3 | 2.4 | |
| T | 1.8 | 1.8 | 1.5 | 1.5 | 1.3 | 1.5 | 1.5 | 1.6 | 1.4 | 1.7 |
Настройки ПИ-регулятора определить по формульному методу:
| Регулятор | Апериодический процесс | Процесс с перерегулированием 20 % | Процесс с минимальным временем регулирования |
| ПИ | 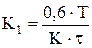 , , 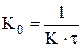 | 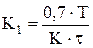 , , 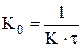 | 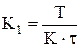 , , 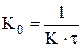 |
Порядок выполнения работы
1. Ознакомиться с краткими теоретическими сведениями и примерами.
2. Выполнить зада

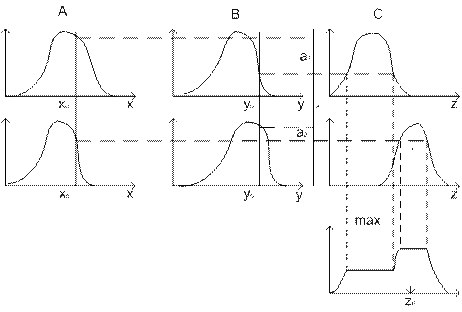 Рисунок 3.1 – Графическая интерпретация алгоритма Мамдани
Рисунок 3.1 – Графическая интерпретация алгоритма Мамдани