Основные положения метода конечных элементов

Рама тележки представляет собой сложную статически неопределимую пространственную конструкцию с переменным сечением составляющих ее элементов. Расчет прочности такой конструкций классическими методами сопротивления материалов требует большого числа ручных вычислений. В частности при расчете рамы методом сил [ ] необходимо выбрать основную и эквивалентную системы, записать канонические уравнения метода сил и определить их коэффициенты, построить эпюры единичных сил, перемножить эпюры моментов заданных сил на соответствующие единичные эпюры. Кроме того, расчет прочности таким методом не дает общей картины распределения внутренних силовых факторов при сложном нагружении и не позволяет достаточно точно учесть влияние концентраторов напряжений – переходов сечений, угловых стыков, отверстий и т.д. Все это, в конечном счете, приводит к необходимости назначения завышенных запасов прочности и как следствие увеличению материалоемкости конструкции. В настоящее время стремление к повышению скоростей движения, особенно в пассажирских перевозках, требует снижения массы подвижного состава и в частности его ходовых частей. Одним из путей снижения массы без снижения прочностных показателей является создание так называемых равнопрочных конструкций, т.е. конструкций у которых внутренние напряжения от внешних нагрузок примерно одинаковы по всему объему. Создание таких конструкций в первую очередь требует качественно новых методов расчета, позволяющих максимально точно учитывать геометрические параметры и физические свойства материала рассматриваемого объекта.

Одним из таких методов, который стал альтернативой классическим методам расчета прочности является метод конечных элементов [ ] теоретические и прикладные аспекты, которого получили развитие во второй половине ХХ века.

Ключевая идея метода конечных элементов при анализе поведения конструкций заключается в следующем: сплошная среда моделируется путем разбиения ее на области (конечные элементы), в каждой из которых поведение среды описывается с помощью отдельного набора выбранных функций, представляющих перемещения и напряжения в заданной области. Таким образом, метод конечных элементов основан на аппроксимации непрерывной функции (напряжения, перемещения, температуры) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей.

Предположим, что состояние системы описывается некоторой функцией. Эта функция является единственным решением задачи сформулированной на основе физических законов. Решение состоит в отыскании из бесконечного множества функций такой функции, которая удовлетворяет уравнениям задачи. Для сложных задач связанных с расчетом прочности элементов подвижного состава найти точное решение, как правило, невозможно. Поэтому вместо отыскания требуемой функции, задача упрощается. Рассматривается некоторое семейство функций определяемых конечным числом параметров. Как правило, среди этих функций нет точного решения, однако соответствующим подбором параметров можно приближенно удовлетворить условиям задачи, т.е. построить ее приближенное решение.

Допустим, требуется построить такое семейство функци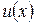й при 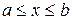. Интервал 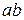разбивается на конечное число частей (элементов), соединенных между собой и с концами интервала в узловых точках 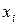. В пределах каждого элемента задается функция, например в виде линейного полинома. Она определяется своими значениями 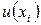в узлах на концах элемента. Если отыскиваемая функция является непрерывной, то ее значения в каждом узле для соседних элементов совпадают. В результате имеем семейство кусочно-линейных непрерывных функций, которые изображаются в виде ломанных и определяются конечным числом параметров – своими узловыми значениями. На рис. 6.2 показан пример кусочно-линейной функции, она имеет 5 элементов, 6 узлов и 6 узловых параметров .

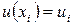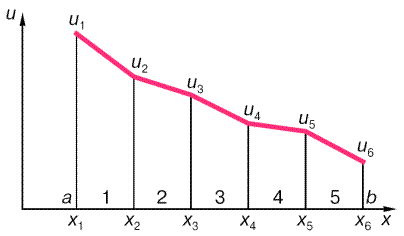
Рис. 6.2. Кусочно-линейная функция

Следовательно, метод конечных элементов заменяет задачу нахождения функции на задачу нахождения конечного числа ее приближенных значений в отдельных точках.

С уменьшением максимального размера элементов увеличивается число узлов и неизвестных узловых параметров. Вместе с тем повышается возможность более точно удовлетворить уравнениям задачи и приблизится к искомому решению (рис. 6.3).

В качестве преимуществ метода конечных элементов можно отметить следующее [ ]:

1. Свойства материалов смежных элементов могут быть неодинаковыми. Это позволяет применять метод к конструкциям из разнородных материалов.

2. Криволинейная область может быть достаточно точно аппроксимирована с помощью прямолинейных элементов, как это показано на рис. 6.3.

3. Размеры элементов могут быть переменными. Это позволяет уплотнять сетку в отдельных областях (например, вблизи концентраторов напряжений) для получения более точных результатов.

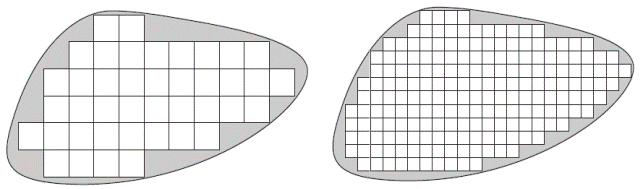
Рис. 6.3. Влияние размера элементов на точность аппроксимации.

При решении задач методом конечных элементов используются элементы различной конфигурации и размерности. Рассмотрим наиболее часто используемые типы элементов.

Простейшим элементом является одномерный элемент. Схематически он изображается в виде отрезка (рис. 6.4, а), хотя и имеет поперечное сечение. Площадь поперечного сечения может изменяться по длине, но в большинстве случаев она принимается постоянной. Такой элемент используется в одномерных задачах распространения тепла и в задачах строительной механики при расчете стержневых элементов конструкций. Простейший одномерный элемент имеет два узла, по одному на каждом конце. Существуют элементы и более высокого порядка, трехузловые (квадратичные) и четырехузловые (кубические) (рис. 6.4, б, в). Одномерные элементы могут быть криволинейными при условии, что длина дуги входит в определяющие их уравнения.

Рис. 6.4. Одномерные конечные элементы

Для построения дискретной модели двумерной области используются два основных семейства элементов – треугольники и четырехугольники. Стороны линейных элементов каждого семейства представляют собой прямые линии (рис. 6.5, а, г). Квадратичные и кубические элементы могут иметь как прямолинейные, так и криволинейные стороны (рис. 6.5, б, в, д) или те и другие (рис. 6.5, е). Возможность моделирования криволинейных границ достигается добавлением узлов в середину сторон элементов. Толщина элемента может быть постоянной или являться функцией координат.

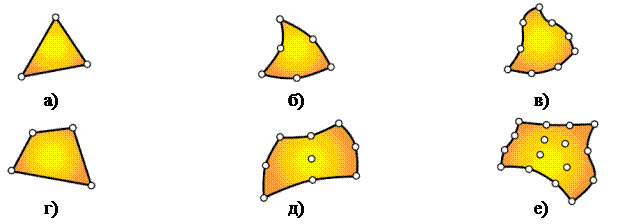
Рис. 6.5. Двумерные конечные элементы

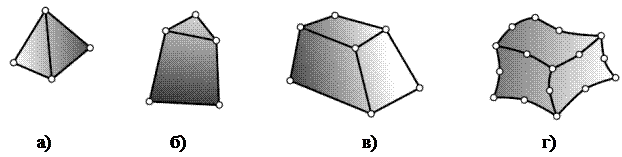Наиболее часто используемыми трехмерными элементами являются пирамида, тетраэдр и параллелепипед (рис. 6.6, а, б, в). Линейные элементы ограничены прямолинейными плоскостями. Элементы более высокого порядка могут иметь в качестве границ криволинейные поверхности (рис. 6.6, г).

Рис. 6.6. Трехмерные конечные элементы

Практическое использование метода конечных элементов во многих областях инженерной деятельности стало возможным с развитием вычислительной техники. Сейчас применение специализированных программных пакетов для расчета методом конечных элементов прочности конструкций имеющих сложную геометрическую конфигурацию и нерегулярную физическую структуру стало, стандартом во многих отраслях машиностроения и в том числе в локомотивостроении.