Что учитывают перед проведением шаговой оптимизации (априорная)?

Сравнивают результаты опыта с предыдущими. Эта основа шаговой оптимизации

При шаговой оптимизации поиск оптимума проводят с постоянным шагом.

Шаг – приращение независимой переменной. При его выборе учитывают:

1. физико- хим. св-ва системы;

2. особенности технологии и методов измерения;

3. имеющиеся данные

Все указанные данные до проведения опыта назыв. априорной информацией.

Недостаток шаговой оптимизации?

Пусть К_ОПТ явл. функцией одной переменной х. Первый опыт поставлен при х=х₁, далее проводится произвольный шаг, например в сторону увеличения; при х₂ получаем следующее значение К_ОПТ. Сравниваются результаты х₁ и х₂. Так как при х₂ К_ОПТ больше, то последующее значения х₃ и х₄ выполнены в сторону их увеличения с постоянным шагом.

Получая значения К_ОПТ при х₇ и х₈ близки по значению, разность меду ними значениями К_ОПТ (х₇) и К_ОПТ (х₈) могут быть равны ошибке опыта. В этом заключается трудность определения К_ОПТ явл. недостатком шаговой оптимизации

Суть метода Гаусса- Зейделя?

Экстремум функции нескольких переменных. Метод Гаусса - Зейделя

Рассмотрим выход продукта зависящий от Р и Т (давление и температура)

β = f (P, T)

График этой зависимости нам не известен.

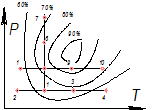
1.При фиксированной Р проводится серия опытов 1,2-4. Предпочтения из 1-го и 3-го опытов отдается опыту 1, т.к. получен при меньшей температуре.

2. Фиксируется температура и проводится при постоянном температуре опыты 5,6,7.

3. При постоянном давлении соответствующему опыту 5 проводятся опыты 8,9,10. 9-й опыт обеспечивает выход продукта 90%, если этот результат удовлетворяет, то оптимизация заканчивается.

Недостаток метода Гаусса-Зейделя?

Большое число опытов для достижения экстремума

Суть метода Бокса – Уилсона?

Последовательность опред. оптимума:

Проводится опыт 1 и около этой точки с небольшими отклонениями значения P_i проводятся опыты 1 ^/ и 1 ^// и 1 ^///. По результатам 5-ти опытов выводится уравнение плоскости.

2. При значениях P_i близких к опыту 3 проводятся опыты 3 ^/ 3 ^// 3 ^/// Описываются результатом уравнения 1 и точек возрастания. Направление функции аналогично пункту 1.

3. Значение опытов 10-11 не дают однозначного ответа оптимума. Для поиска экстремума функции используют уже описание функции полиномов n-й степени.

Определение градиента?

Градиент – это вектор направленный в сторону в которую величина У возрастает в большую сторону для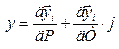

Суть метода множителей Лагранжа?

метод решения задач на условный экстремум; метод заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.

Когда используют метод Лагранжа?

Этот метод используется если на переменные параметры целевой функции наложены ограничения типа равенства нулю.

Система уравнений по Лагранжу?

Чтобы определить экстремальные значения точки целевой функции Fк необходимо решить систему уравнений. Система получается если взять одну производную от вспомогательной функции и по всем неизвестным параметрам Х, а так же по всем множителям Лагранжа λ и после этого приравнять их к нулю.

Что явл. стадией при динамическом программировании?

В качестве стадии можно принять единицу времени.

Требования к процессу при динамическом программировании?

1.Оптимизированный процесс должен быть дискретно распределенным во времени или пространстве.

2.Отдельные стадии процесса должны обладать относительной независимостью, т.е. выходные параметры стадии зависят только от выходных параметров на эту стадию.

3. Критерий оптимальности всего процесса, есть аддитивная функция критерия оптимальности каждой стадии.