Выбор и характеристика языка программирования

Для выполнения данного задания бы использован язык программирования Pascal ABC.NET.

Pascal ABC.NET — это:

Язык программирования Pascal нового поколения, сочетающий простоту классического языка Паскаль, ряд современных расширений и огромные возможности платформы .NET.

Бесплатная, простая и мощная среда разработки.

Встроенный в среду разработки дизайнер форм, позволяющий быстро создавать оконные приложения.

Уникальная Web-среда, позволяющая разрабатывать и запускать программы на языках Pascal ABC.NET, C#, Visual Basic.NET, F#, IronPython из окна браузера, а также иметь личный каталог программ на сервере.

Ключевые особенности Pascal ABC.NET

Ряд расширений языка Pascal, в числе которых оператор foreach, внутриблочные описания переменных, автоопределение типа при описании, встроенные множества произвольных типов, упрощенный синтаксис модулей, методы в записях, операция new для создания объектов, определение тел методов внутри классов, безымянные классы, автоклассы, целые произвольной длины.

Самые современные средства языков программирования: обобщенные классы и подпрограммы, интерфейсы, перегрузка операций, λ-выражения, исключения, сборка мусора, n-мерные динамические массивы.

Генерация эффективного кода для платформы .NET.

Высокая совместимость с Delphi.

Высокая скорость выполнения программ.

Возможность доступа к огромному количеству .NET-библиотек от контейнерных классов до средств работы с сетью.

Среда разработки с встроенным отладчиком, обеспечивающая подсказки по коду, переход к определению и реализации подпрограммы, шаблоны кода, автоформатирование кода.

Встроенный в среду разработки дизайнер форм для быстрого создания оконных приложений.

Простая и эффективная растровая графическая библиотека.

Средства параллельного программирования в виде директив OpenMP.

Встроенный электронный задачник ProgrammingTaskbook.

Модули исполнителей Робот и Чертежник, используемых в школьной информатике.

Механизм проверяемых заданий, обеспечивающий автоматическую постановку и проверку заданий.

Наличие Web-среды разработки WDE, позволяющей запустить программу прямо из окна браузера.

Возможность опубликовать в интернете ссылку на файл, сохраненный в Web-среде разработки.

Возможность запуска консольного компилятора под Mono в современных версиях Linux.

Использование многолетнего опыта обучения программированию при создании языка и среды.

Система Pascal ABC.NET является совместной разработкой российских и немецких программистов. В России центр разработки находится на факультете математики, механики и компьютерных наук Южного федерального университета.

Pascal ABC.NET активно используется в ряде средних и высших учебных заведений России и ближнего зарубежья. Так, на мехмате Южного федерального университета он используется как основной язык для обучения студентов направления Информационные технологии в курсе Основы программирования, а также для обучения школьников в одной из самых больших в России Детской компьютерной школе.

Програмная реализация

const eps=0.001; //эпсилон погрешность

function function1(x:real):real; // функция x4-3x+1=0

begin

function1:=power(x,4)-3*x+1;//

end;

function diff1_func1(x:real):real; //первая производная первой функции

begin

diff1_func1:= 4*x*x*x;

end;

function diff2_func1(x:real):real; //вторая производная первой функции

begin

diff2_func1:=12*x;

end;

function function2(x:real):real; //функция lgx-10^-x=0

begin

function2:=log10(x)-1/power(10,x);

end;

function diff1_func2(x:real):real; //первая производная второй функции

begin

diff1_func2:= (1/(x*ln(10)))+power(10,-x)*ln(10);

end;

function diff2_func2(x:real):real; //вторая производная второй функции

begin

diff2_func2:=x*(ln(10)-1/10)-ln(10)-power(10,-x)*(ln(10)*ln(10)-1/10);

end;

procedure dichotomy(var a,b:real); //метод дихотомии

var t,f1,f2,x:real;

iteration: integer;

begin

iteration:=0;

repeat

t:=(a+b)/2;

f1:=function1(a);

f2:=function1(t);

if (f1*f2<=0) then b:=t

else

begin

a:=t;

f1:=f2;

end;

iteration:=iteration+1;

until abs(b-a)<=eps;

x:=(a+b)/2;

writeln('Корень: x = ',x:10:6);

writeln('Функция: f(x) = ',function1(x));

writeln('Кол-во итераций: ',iteration);

end;

procedure chord(var a,b:real); //метод хорд

var f,f2,fz,z,x,h:real;

iteration: integer;

begin

iteration:=0;

f:=function1(a);

f2:=diff2_func1(a);

if (f*f2>0) then

begin

x:=b;

z:=a;

end

else

begin

x:=a;

z:=b;

end;

fz:=function1(z);

repeat

f:=function1(x);

h:=((x-z)*f)/(f-fz);

x:=x-h;

iteration:=iteration+1;

until (abs(h)<=eps);

writeln('Корень: x = ',x:10:6);

writeln('Функция: f(x) = ',function1(x):1:13);

writeln('Кол-во итераций: ',iteration);

end;

procedure newton(var a,b:real); //метод Ньютона

var f,f1,f2,x,h:real;

iteration: integer;

begin

iteration:=0;

f:=function2(b);

f2:=diff2_func2(b);

if (f*f2>0) then x:=b else x:=a;

repeat

f:=function2(x);

f1:=diff1_func2(x);

h:=f/f1;

x:=x-h;

iteration:=iteration+1;

until (abs(h)<=eps);

writeln('Корень: x = ',x:10:6);

writeln('Функция: f(x) = ',function2(x):1:13);

writeln('Кол-во итераций: ',iteration);

end;

function phix(var x,lamb:real):real; //дополнительная функция fi(x)

begin

phix:=x-lamb*(log10(x)-power(10,-x));

end;

procedure iterations(var a,b:real); //метод простых итераций

var iteration:integer;

x,x0,lamb:real;

begin

iteration:=0;

x:=(a+b)/2;

if (diff1_func2(a)>diff1_func2(b)) then lamb:=1/diff1_func2(a)

else lamb:=1/diff1_func2(b);

repeat

x0:=x;

x:=phix(x0,lamb);

iteration:=iteration+1;

until (abs(x-x0)<=eps);

writeln('Корень: x = ',x:10:6);

writeln('Функция: f(x) = ',function2(x):1:13);

writeln('Кол-во итераций: ',iteration);

end;

BEGIN

var a,b:real;

a:=0.1; //функция имеет два корня, поэтому вычисляем на двух промежутках

b:=1; //границы первого промежутка

writeln('Первая функция: x^4-3*x+1');

writeln;

writeln('Метод дихотомии');

dichotomy(a,b);

writeln;

a:=1; //границы второго промежутка

b:=1.5;

dichotomy(a,b);

writeln;

a:=0.1; //границы первого промежутка

b:=1;

writeln('Метод хорд');

chord(a,b);

writeln;

a:=1; //границы второго промежутка

b:=1.5;

chord(a,b);

writeln();

writeln('Вторая функция: lg(x)-10^-x');

writeln;

writeln('Метод Ньютона');

newton(a,b);

writeln;

writeln('Метод простых итераций');

a:=0.1;

b:=1.5;

iterations(a,b);

END.

Анализ результатов расчета.

Границы интервала: а = 0.1, b = 1.5.

Метод дихотомии:

x₁ = 0.337744, количество итераций = 10

x₂ = 1.307129, количество итераций = 9

Метод хорд:

x₁ = 0.337674, количество итераций = 4

x₂ = 1.307306, количество итераций = 6

Метод Ньютона:

x = 1.168905, количество итераций = 4

Метод итераций:

x = 1.167165, количество итераций = 11

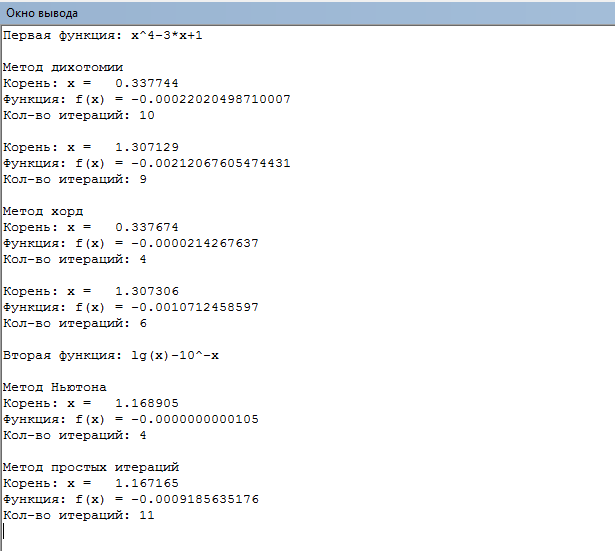
Рисунок 14 - Демонстрация работы программы

Вывод

Были рассмотрены методы уточнения действительных корней при решении нелинейных уравнений, а именно:

1. Метод половинного деления;

2. Метод простых итераций;

3. Метод Ньютона (метод касательных);

4. Метод хорд.

Была разработана программа, реализующая вышеперечисленные методы с точностью 0.0001, с помощью среды программирования Pascal ABC.NET.

Разработанная программа находит действительные корни для уравнений:

x⁴-3x+1=0

lgx=10^-x

Для уравнения x⁴-3x+1=0 действительные корни находятся при помощи методов дихотомии и хорд.

Результаты выполнения программы показали, что метод хорд выполняется за минимальное число итераций.

Для уравнения lgx=10^-x действительные корни находяться при помощи методов простых итераций и Ньютона.

Результаты выполнения программы показали, что метод Ньютона выполняется за минимальное число итераций.